Bhagya

MP Board Class 6th Maths Solutions Chapter 8 Decimals Ex 8.6

Question 1.
Subtract:
(a) Rs. 18.25 from Rs. 20.75
(b) 202.54 m from 250 m
(c) Rs. 5.36 from Rs. 8.40
(d) 2.051 km from 5.206 km
(e) 0.314 kg from 2.107 kg
Solution:

Question 2.
Find the value of:
(a) 9.756 – 6.28
(b) 21.05 – 15.27
(c) 18.5 – 6.79
(d) 11.6 – 9.847
Solution:

Question 3.
Raju bought a book for Rs. 35.65. He gave Rs. 50 to the shopkeeper. How much money did he get back from the shopkeeper?
Solution:
Total amount given to shopkeeper = Rs. 50
Cost of book = Rs. 35.65
Amount left = Rs. 50.00 – Rs. 35.65 = Rs. 14.35
Therefore, Raju got back Rs. 14.35 from the shopkeeper.

Question 4.
Rani had Rs. 18.50. She bought one ice-cream for Rs. 11.75. How much money does she have now?
Solution:
Total money = Rs. 18.50
Cost of ice-cream = Rs. 11.75
Amount left = Rs. 18.50 – Rs. 11.75 = Rs. 6.75
Therefore, Rani has Rs. 6.75 now.

Question 5.
Tina had 20 m 5 cm long cloth. She cuts 4 m 50 cm length of cloth from this for making a curtain. How much cloth is left with her?
Solution:
Total length of cloth = 20 m 5 cm = 20.05 m
Length of cloth used = 4 m 50 cm = 4.50 m
Remaining cloth = 20.05 m – 4.50 m = 15.55 m
Therefore, 15.55 m of cloth is left with Tina.

Question 6.
Namita travels 20 km 50 m every day. Out of this she travels 10 km 200 m by bus and the rest by auto. How much distance does she travel by auto?
Solution:
Total distance travelled = 20 km 50 m = 20.050 km
Distance travelled by bus = 10 km 200 m = 10.200 km
Distance travelled by auto = (20.050 – 10.200) km = 9.850 km
Therefore, 9.850 km distance is travelled by auto.

Question 7.
Aakash bought vegetables weighing 10 kg. Out of this, 3 kg 500 g is onions, 2 kg 75 g is tomatoes and the rest is potatoes. What is the weight of the potatoes?
Solution:
Weight of onions = 3 kg 500 g = 3.500 kg
Weight of tomatoes = 2 kg 75 g = 2.075 kg
Total weight of onions and tomatoes
= (3.500 + 2.075) kg = 5.575 kg
Therefore, weight of potatoes
= (10.000 – 5.575) kg = 4.425 kg
Thus, weight of potatoes is 4.425 kg.

MP Board Class 6th Maths Solutions

MP Board Class 6th Hindi Bhasha Bharti Solutions Chapter 12 डॉ. होमी जहाँगीर भाभा

MP Board Class 6th Hindi Bhasha Bharti Chapter 12 पाठ का अभ्यास

प्रश्न 1.
सही विकल्प चुनकर लिखिए

(क) भाभा अणु-शक्ति संस्थान स्थित है
(i) चेन्नई में
(ii) ट्राम्बे में,
(iii) इंग्लैण्ड में,
(iv) जिनेवा में।
उत्तर
(ii) ट्राम्बे में,

(ख) डॉ. भाभा को पी-एच.डी की उपाधि मिली
(i) सन् 1941 में,
(ii) सन् 1947 में,
(iii) सन् 1951,
(iv) सन् 1966 में।
उत्तर
(i) सन् 1941 में।

प्रश्न 2.
रिक्त स्थानों की पूर्ति कीजिए

(क) डॉ. भाभा के पिता का नाम …………था।
उत्तर
श्री जे०एस०भाभा

(ख) डॉ. भाभा …………… से संगीत सुनते थे।
उत्तर
ग्रामोफोन।

प्रश्न 3.
एक या दो वाक्यों में उत्तर दीजिए

(क) भारत में अणुशक्ति का विकास किसने किया ?
उत्तर
भारत में अणु शक्ति का विकास प्रथम वैज्ञानिक डॉ. होमी जहाँगीर भाभा ने किया।

(ख) विज्ञान में रुचि के अलावा डॉ. भाभा की और कौन-कौन सी विशेषताएँ थीं?
उत्तर
डा० भाभा को गणित और भौतिक विज्ञान से अति प्रेम था, उन्होंने विद्युत एवं चुम्बक सम्बन्धी बातों के अतिरिक्त कॉस्मिक किरण की मौलिक खोजों पर भाषण दिए। उन्हें संगीत, नृत्य एवं चित्रकला से भी भारी लगाव था। वे पेड़-पौधों और बगीचों के बड़े शौकीन थे।

(ग) डॉ. भाभा की एकमात्र इच्छा क्या थी?
उत्तर
डॉ. भाभा की एकमात्र इच्छा थी कि भारत को आने वाले वर्षों में आणविक शक्ति के कार्यों के लिए दूसरों का मुँह न ताकना पड़े।

(घ) चित्रकार ने डॉ. भाभा के बनाए चित्र को देखकर क्या कहा था?
उत्तर
चित्रकार ने डॉ. भाभा के बनाए चित्र को देखकर कहा था कि एक दिन यह बालक महान कलाकार बनेगा।

(ङ) अणुशक्ति के रचनात्मक प्रयोग के लिए कौन-सी संस्था स्थापित की गई ?
उत्तर
अणुशक्ति के रचनात्मक प्रयोग के लिए मुम्बई में सर दोराबजी-टाटा ट्रस्ट द्वारा “टाटा इन्स्टीट्यूट ऑफ फंडामेन्टल रिसर्च” नामक संस्था स्थापित की गई।

प्रश्न 4. तीन से पाँच वाक्यों में उत्तर दीजिए

(क) डॉ. भाभा को संगीत के प्रति लगाव कैसे उत्पन्न हुआ?
उत्तर
डॉ.भाभा को बचपन में नींद नहीं आती थी। वे प्रायः रोते रहते थे। इससे पिता को बड़ी चिन्ता लग गई। उन्होंने डॉक्टर की सलाह ली। उनकी सलाह पर डॉ. भाभा के सामने ग्रामोफोन बजाया जाने लगा। इससे उनका ध्यान बँट जाता और वे चुप हो जाते थे। फलतः उनको संगीत के प्रति लगाव हो गया।

(ख) अणुशक्ति के बारे में डॉ. भाभा के क्या विचार थे?
उत्तर
डॉ. भाभा अणुशक्ति से अणुबम बनाने के पक्ष में नहीं थे। अणुबम से लाखों लोगों की जान चली जाती है। इसलिए वे अणुशक्ति का प्रयोग शांतिपूर्ण एवं रचनात्मक कार्यों के लिए करना चाहते थे।

(ग) डॉ. भाभा की शिक्षा कहाँ-कहाँ हुई ?
उत्तर
मुंबई विश्वविद्यालय से ई.एम.सी. की परीक्षा पास करके वे आगे की पढ़ाई के लिए इंग्लैण्ड चले गए। वहाँ इंजीनियरिंग की परीक्षा पास करके गणित और भौतिक विज्ञान की शिक्षा के लिए उन्होंने कैम्ब्रिज केयस कॉलेज में प्रवेश लिया। उसी मध्य उन्होंने यूरोप के विभिन्न देशों में जाकर विद्युत एवं चुम्बक तथा कॉस्मिक किरण की मौलिक खोज पर अपने भाषण दिए। उन्हें लन्दन की रॉयल सोसाइटी का फैलो चुना गया। पी-एच. डी. तथा डी.एस-सी की उपाधियाँ विभिन्न विश्वविद्यालयों से प्राप्त हुई।

(घ) डॉ. भाभा की मृत्यु कैसे हुई ?
उत्तर
24 जनवरी, 1966 को भारतीय विमान सेवा का ‘कंचनजंघा’ नामक जेट विमान मुम्बई से जिनेवा जा रहा था। इसी विमान से डॉ. भाभा भी यात्रा कर रहे थे। जिनेवा के पास एक बहुत ऊँचा पहाड़ है ‘माउन्ट ब्लॉक’ इस पहाड़ से वह विमान टकरा कर गिर गया। इस दुर्घटना में डॉ.भाभा की मृत्यु हो गई।

प्रश्न 5.
सोचिए और बताइए

(क) अणुशक्ति का प्रयोग विकास के कार्यों में किस प्रकार हो सकता है ?
उत्तर
अणुशक्ति के प्रयोग से बिजली प्राप्त की जा सकती है। इंजन चलाए जा सकते हैं। कल-कारखानों की बड़ी-बड़ी मशीनें चलाई जा सकती हैं। उजाला किया जा सकता है। रेलगाड़ियाँ चलायी जा सकती हैं। खेती के लिए विद्युत से पानी खींचा जा सकता है। अणुशक्ति से अनेक रोगों के इलाज में सहायता मिल सकती है। लोगों के लिए अनेक वैज्ञानिक प्रयोगों में इससे ऊर्जा प्राप्त की जा सकती है। आवागमन, स्वच्छता, चिकित्सा आदि सम्बन्धी सुविधाएँ ली जा सकती हैं।

(ख) किसी कार्य से ध्यान बंटाने के लिए कौन-कौन से उपाय किए जा सकते हैं?
उत्तर
ऐसे अनेक कार्य हैं जिनके द्वारा किसी काम से ध्यान हटाया जा सकता है, जैसे-

1. संगीत सुनना
2. चित्रकारी करना
3. पेड़ पौधों की सिंचाई-गुड़ाई करना व कलात्मक क्रियाएँ करना
4. शास्त्रीय और आधुनिक संगीत सीखना तथा
5. प्राकृतिक रूप से आकर्षक स्थलों पर घूमना-फिरना।

(ग) विमान दुर्घटनाएँ किन-किन कारणों से हो सकती
उत्तर
विमान दुर्घटनाएँ प्रायः इंजन में खराबी होने से हो सकती, हैं। परन्तु कभी-कभी पर्वतीय क्षेत्रों के मध्य से या ऊपर से गुजरने पर उन स्थलों की बनावट व ऊँचाई का सही ज्ञान न होने पर दुर्घटना होती है। आकाश में उड़ते पक्षियों से टकराने से विमान असन्तुलित होकर गिर जाते हैं। इंजन में आग लग जाती है। पेट्रोल ट्रैक के अचानक फट जाने से भी दुर्घटना होती है। तेज तूफान आने पर कुहरा या धुंध छाये रहने से दृष्टिबाधित होने की स्थिति में विमान दुर्घटनाएं हो जाती हैं। रडार यंत्र की खराबी से विमान सम्पर्क टूट जाने पर विमान भटक कर टकरा जाते हैं और दुर्घटनाएं हो जाती हैं।

प्रश्न 6.
अनुभव और कल्पना के आधार पर उत्तर दीजिए

(क) यदि 15 वर्ष की आयु में ही डॉ. होमी जहाँगीर भाभा को यूरोप में शिक्षा प्राप्त करने का अवसर मिल जाता तो उनके व्यक्तित्व में क्या परिवर्तन होते ? .
उत्तर
यदि 15 वर्ष की आयु में ही डॉ. भाभा को यूरोप में शिक्षा के लिए भेज दिया जाता तो वे थोड़े समय में ही विज्ञान सम्बन्धी शिक्षा प्राप्त करके भारत लौट आते और अपनी प्रशंसनीय सेवाओं को देश को समर्पित करते। देश विविध क्षेत्रों में प्रगति करता और विश्व में अपने विकास से एक विशेष स्थान बना पाता।

(ख) यदि डॉ. भाभा का दुर्घटना में निधन नहीं होता तो अणुशक्ति के उनके शान्तिपूर्ण प्रयासों का विश्व पर क्या प्रभाव पड़ता?
उत्तर
यदि डॉ. भाभा का दुर्घटना में निधन नहीं होता तो उनकी अणुशक्ति के शान्तिपूर्ण प्रयासों का विश्व पर यह प्रभाव | पड़ता कि उस शक्ति का विनाशकारी रूप (बम) के निर्माण में प्रयोग नहीं किया जाता। देशों में अपनी सुरक्षा के नाम पर बनने वाले विध्वंसक यंत्र नहीं बनते। विश्व में पर्यावरणीय समस्या नहीं आती। पानी-हवा आदि स्वच्छ रहते। अनेक रोगों से मुक्ति मिलती। विश्व के देश अपेक्षाकृत विकसित होते, सुख और शान्ति होती। लोग समृद्ध, स्वस्थ और सुखी होते।

भाषा की बात

प्रश्न 1.
निम्नलिखित शब्दों का उच्चारण कीजिएअन्तर्राष्ट्रीय, ट्रॉम्बे, अलंकृत, सौन्दर्यपूर्ण, इंस्टीट्यूट।
उत्तर
अपने अध्यापक महोदय के सहयोग से शुद्ध उच्चारण कीजिए और अभ्यास कीजिए।

प्रश्न 2.
पाठ में आए शब्द-युग्मों को छाँटकर लिखिए।
उत्तर
अणु-शक्ति, पढ़े-लिखे, संगीत-प्रेमी।

प्रश्न 3.
निम्नलिखित शब्दों के दो-दो पर्यायवाची शब्द लिखिए
(i) संसार
(ii) उपवन
(iii) दीप
(iv) मार्ग।
उत्तर
(i) संसार-जग, जगत, विश्व, दुनिया।
(ii) उपवन-बाग, बगीचा।
(iii) दीप-दीया, दीपक।
(iv) मार्ग-पथ, राह, रास्ता।

प्रश्न 4.
दिए गए शब्दों में त्व, इत, ईय प्रत्यय जोड़कर नए शब्द बनाइए
प्रभु, पशु, नारी, पुष्प, सम्मान, प्रभाव, दर्शन, राष्ट्र, भारत।
उत्तर

1. प्रभु + त्व = प्रभुत्व, पशु + त्व = पशुत्व, नारी + त्व = नारीत्व।
2. पुष्प + इत=पुष्पित, सम्मान + इत = सम्मानित, प्रभाव + इत = प्रभावित।
3. दर्शन + ईय = दर्शनीय, राष्ट्र + ईय = राष्ट्रीय, भारत + ईय = भारतीय।

प्रश्न 5. उपसर्ग जोड़कर नए शब्द बनाइए
उपसर्ग-अ, सु, दुर्।
शब्द-शुभ, ज्ञान, सभ्य, मार्ग, गंध, संस्कृत, जन, गति,
उत्तर

1. अ+ शुभ-अशुभ, अ + ज्ञान = अज्ञान, अ + सभ्य = असभ्य।
2. सु + मार्ग = सुमार्ग, सु + गंध = सुगंध, सु + संस्कृत = सुसंस्कृत।
3. दुर् + जन् = दुर्जन, दुर् + गति = दुर्गति, दुर् + गुण = दुर्गुण।

प्रश्न 6.
निम्नलिखित शब्दों के तत्सम रूप लिखिए
(i) घर
(ii) खेत
(iii) लाज।
उत्तर
(i) घर = गृह
(ii) खेत = क्षेत्र
(iii) लाज = लज्जा।

प्रश्न 7.
निम्नलिखित शब्दों का वाक्यों में प्रयोग कीजिए
(1) अणु-शक्ति
(2) संगीत-प्रेमी
(3) वैज्ञानिक
(4) सपूत।
उत्तर

1. अणुशक्ति-डॉ. भाभा ने अणु-शक्ति का प्रयोग विकास और शान्ति के कार्यों के लिए उपयोग करने की सलाह दी।
2. संगीत-प्रेमी-डॉ. भाभा बचपन से ही संगीत-प्रेमी थे।
3. वैज्ञानिक-विश्व के प्रसिद्ध वैज्ञानिकों द्वारा डॉ. भाभा को स्मरण किया जाता है।
4. सपूत-डॉ. भाभा भारत माता के वह सपूत थे जिन्होंने सदैव चाहा कि अणुशक्ति का उपयोग केवल मानव कल्याण के लिए किया जाये।

प्रश्न 8.
निम्नलिखित वाक्यों में से मुख्य क्रिया और सहायक क्रिया छाँटकर लिखिए
(क) गोपाल स्कूल जाता है।
(ख) वह पुस्तक पढ़ चुका है।
(ग) सौता पत्र लिख रही है।
(घ) राम स्कूल गया था।
उत्तर
(क) ‘जाना’ मुख्य क्रिया, ‘है’ सहायक क्रिया।
(ख) ‘पढ़ना’ मुख्य क्रिया, ‘है’ सहायक क्रिया।
(ग) “लिखना’ मुख्य क्रिया, ‘है’ सहायक क्रिया।
(घ) ‘जाना’ मुख्य क्रिया, था’ सहायक क्रिया।

डॉ. होमी जहाँगीर भाभा परीक्षोपयोगी गद्यांशों की व्याख्या 

(1) डॉक्टर भाभा अणु-शक्ति से अणुबम बनाने के पक्ष में नहीं थे। अणुबम से लाखों लोगों की जान चली जाती है। इसलिए वे अणु-शक्ति का प्रयोग शांतिपूर्ण, रचनात्मक कार्यों के लिए करना चाहते थे।

सन्दर्भ – प्रस्तुत गद्यांश हमारी पाठ्यपुस्तक ‘भाषा भारती’ के’डॉ. होमी जहाँगीर भाभा’ नामक पाठ से लिया गया है। इसके लेखक डॉ. सुखदेव दुबे व अन्य लेखकगण हैं।

प्रसंग-प्रस्तुत गद्यांश में डॉ. भाभा की दूरदर्शिता का वर्णन किया गया है।

व्याख्या-डॉ. होमी जहाँगीर भाभा अणु’ की शक्ति को पहचानते थे। साथ ही, वह यह भी जानते थे कि ‘अणुबम’ के रूप में इसकी ताकत का गलत उपयोग, मानव सभ्यता के लिए काफी खतरनाक होता है। अणुबम के विध्वंस से पलभर में हजारों-लाखों जिन्दगियाँ काल के गाल में समा जाती हैं। अत: वे अणु-शक्ति का सही उपयोग करके इस विलक्षण ‘ऊर्जा’ को मानव की सेवा में तथा शांतिपूर्ण एवं रचनात्मक कार्यों में लगाना चाहते थे।

(2) उनकी कलात्मक रुचि का परिणाम है कि दाम्बे के अणु-शक्ति संस्थान में बगीचे तथा पौधों की सजावट सौन्दर्यपूर्ण एवं कलापूर्ण दिखाई देती है। टाटा इंस्टीट्यूट की गैलरियों तथा कमरों में सजे चित्र एवं वहाँ के उपवन उनकी वैज्ञानिकता एवं कलात्मकता के सुन्दर संगम हैं।

संदर्भ-पूर्व की तरह।

प्रसंग-प्रस्तुत पंक्तियों में डॉ. भाभा की कलात्मकता एवं रुचियों का वर्णन किया है।

व्याख्या-डॉ. भाभा के अन्दर कला के प्रति रुझान था जिसका नतीजा यह है कि उन्होंने अणुशक्ति केन्द्र ट्राम्बे में एक बगीचा विकसित किया है। इस बगीचे कों अनेक पेड़-पौधों से सुन्दर बनाया है, उसकी सजावट में इन्हीं पौधों को विशेष महत्व है। यह सजावट अति कलापूर्ण है। टाटा इन्स्टीट्यट की गैलरियों और अन्य कमरों की सजावट भी चित्रों द्वारा की गई है। ये चित्र भी डॉ. भाभा की कलात्मक रुचि को प्रकट करते हैं। वहाँ के बगीचे और समीप वाले उपवनों के विकास में वैज्ञानिकता झलकती है और उनकी कला का अनोखा जोड़ है, मिश्रण है। इस तरह डॉ. भाभा की वैज्ञानिकता में उनकी कलात्मकता का योग बेजोड़

(3) भारत के इस महान सपूत की स्मृति में ट्रॉम्बे के अणु-शक्ति केन्द्र का नाम बदलकर ‘भाभा अणु-शक्ति अनुसन्धान केन्द्र’ कर दिया गया। डॉ. भाभा आज भले ही हमारे बीच न हों परन्तु उन्होंने विज्ञान जगत को जो अमूल्य योगदान दिया है उससे भावी वैज्ञानिकों को सदा मार्गदर्शन मिलता रहेगा।

सन्दर्भ-पूर्व की तरह।

प्रसंग-डॉ. भाभा के द्वारा विज्ञान जगत के लिए किए गए कार्यों का महत्व बताया गया है।

व्याख्या-डॉ. भाभा भारत के बहुत बड़े महत्वपूर्ण पुत्र थे। वे आज इस दुनिया में हमारे बीच नहीं हैं, परन्तु विज्ञान के संसार में उन्होंने जो भी हमारे लिए किया है, उसका महत्व महान है। विज्ञान जगत में किया गया उनका कार्य बेजोड़ है। उनकी यादगार के लिए ही ट्रॉम्बे के अणुशक्ति केन्द्र का नाम बदल दिया है और उसका नाम ‘भाभा अणु-शक्ति अनुसन्धान केन्द, कर दिया गया है। उनके वैज्ञानिक प्रयोगों और खोजों से भविष्य के वैज्ञानिकों को उस क्षेत्र में आगे बढ़ने के लिए दिशा-निर्देशन मिलेगा और मानवता की भलाई होती रहेगी। संसार में सुख-समृद्धि होती रहेगी।

MP Board Class 6th Hindi Solutions

MP Board Class 6th Maths Solutions Chapter 8 Decimals Ex 8.2

Question 1.
Complete the table with the help of these boxes and use decimals to write the number,


Solution:

Question 2.
Write the numbers given in the following place value table in

Solution:

Question 3.
Write the following decimals in the place value table.
(a) 0.29
(b) 2.08
(c) 19.60
(d) 148.32
(e) 200.812
Solution:

Question 4.
Write each of the following as decimals.

Solution:
(a) 20 + 9 + 0.4 + 0.01 = 29.41
(b) 137 + 0.05 = 137.05
(c) 23 + 0.2 + 0.006 = 23.206
(d) 700 + 20 + 5 + 0.09 = 725.09

Question 5.
Write each of the following decimals in words.
(a) 0.03
(b) 1.20
(c) 108.56
(d) 10.07
(e) 0.032
(f) 5.008
Solution:
(a) Zero point zero three
(b) One point two zero
(c) One hundred and eight point five six
(d) Ten point zero seven
(e) Zero point zero three two
(f) Five point zero zero eight

Question 6.
Between which two numbers in tenths place on the number line does each of the given number lie?
(a) 0.06
(b) 0.45
(c) 0.19
(d) 0.66
(e) 0.92
(f) 0.57
Solution:
(a) 0.06 lies between 0 and 0.1.
(b) 0.45 lies between 0.4 and 0.5.
(c) 0.19 lies between 0.1 and 0.2.
(d) 0.66 lies between 0.6 and 0.7.
(e) 0.92 lies between 0.9 and 1.0.
(f) 0.57 lies between 0.5 and 0.6.

Question 7.
Write as fractions in lowest terms.
(a) 0.60
(b) 0.05
(c) 0.75
(d) 0.18
(e) 0.25
(f) 0.125
(g) 0.066
Solution:

MP Board Class 6th Maths Solutions

MP Board Class 6th Maths Solutions Chapter 9 Data Handling Ex 9.4

Question 1.
A survey of 120 school students was done to find which activity they prefer to do in their free time.

Draw a bar graph to illustrate the above data taking scale of 1 unit length = 5 students. Which activity is preferred by most of the students other than playing?
Solution:

Reading story books is preferred by most of the students other than playing.

Question 2.
The number of Mathematics books sold by a shopkeeper on six consecutive days is shown below:

Draw a bar graph to represent the above information choosing the scale of your choice.
Solution:

Question 3.
Following table shows the number of bicycles manufactured in a factory during the years 1998 to 2002. Illustrate this data using a bar graph. Choose a scale of your choice.

(a) In which year were the maximum number of bicycles manufactured?
(b) In which year were the minimum number of bicycles manufactured?
Solution:

(a) In 2002, the maximum number of bicycles were manufactured.
(b) In 1999, the minimum number of bicycles were manufactured.

Question 4.
Number of persons in various age groups in a town is given in the following table.

Draw a bar graph to represent the above information and answer the following questions, (take 1 unit length = 20 thousands)
(a) Which two age groups have same Population?
(b) All persons in the age group of 60 and above are called senior citizens. How many senior citizens are there in the town?
Solution:

(a) Age groups 30 – 44 and 45 – 59 have same population.
(b) 80,000 + 40,000 = 1,20,000 senior citizens are there in the town.

MP Board Class 6th Maths Solutions

MP Board Class 6th Maths Solutions Chapter 9 Data Handling Ex 9.3

Question 1.
The bar graph given alongside shows the amount of wheat purchased by the government during the year 1998 – 2002.

Read the bar graph and write down your observations. In which year was
(a) the wheat production maximum?
(b) the wheat production minimum?
Solution:
(a) In 2002, production of wheat was maximum.
(b) In 1998, production of wheat was minimum.

Question 2.
Observe this bar graph which is showing the sale of shirts in a ready made shop from Monday to Saturday.

Now answer the following questions :
(a) What information does the above bar graph give?
(b) What is the scale chosen on the horizontal line representing number of shirts?
(c) On which day were the maximum number of shirts sold? How many shirts were sold on that day?
(d) On which day were the minimum number of shirts sold?
(e) How many shirts were sold on Thursday?
Solution:
(a) The bar graph shows the sale of shirts in a ready made shop from Monday to Saturday.
(b) 1 unit length = 5 shirts
(c) On Saturday, maximum number of shirts, i.e., 60 shirts were sold.
(d) On Tuesday, minimum number of shirts were sold.
(e) On Thursday, 35 shirts were sold.

Question 3.
Observe this bar graph which shows the marks obtained by Aziz in half-yearly examination in different subjects.

Answer the given questions.
(a) What information does the bar graph give?
(b) Name the subject in which Aziz scored maximum marks.
(c) Name the subject in which he has scored minimum marks.
(d) State the name of the subjects and marks obtained in each of them.
Solution:
(a) The bar graph shows the marks obtained by Aziz in half-yearly examination in different subjects.
(b) Hindi
(c) Social Studies
(d) Hindi – 80, English – 60, Mathematics – 70, Science – 50, Social Studies – 40.

MP Board Class 6th Maths Solutions

MP Board Class 6th Maths Solutions Chapter 8 Decimals Ex 8.1

Question 1.
Write the following as numbers in the given table.

Solution:

Question 2.
Write the following decimals in the place value table.
(a) 19.4
(b) 0.3
(c) 10.6
(d) 205.9
Solution:

Question 3.
Write each of the following as decimals:
(a) Seven-tenths
(b) Two tens and nine-tenths
(c) Fourteen point six
(d) One hundred and two ones
(e) Six hundred point eight
Solution:
(a) Seven-tenths = 7 tenths = \(\frac{7}{10}\) = 0.7
(b) Two tens and nine-tenths = \(2 \times 10+\frac{9}{10}\)
= 20 + 0.9 = 20.9
(c) Fourteen point six = 14.6
(d) One hundred and two-ones = 100 + 2 × 1
= 100 + 2 = 102
(e) Six hundred point eight = 600.8

Question 4.
Write each of the following as decimals:

Solution:

Question 5.
Write the following decimals as fractions. Reduce the fractions to lowest form.
(a) 0.6
(b) 2.5
(c) 1.0
(d) 3.8
(e) 13.7
(f) 21.2
(g) 6.4
Solution:

Question 6.
Express the following as cm using decimals.
(a) 2 mm
(b) 30 mm
(c) 116 mm
(d) 4 cm 2 mm
(e) 162 mm
(f) 83 mm
Solution:

Question 7.
Between which two whole numbers on the number line are the given numbers lie?
Which of these whole numbers is nearer the number?

Solution:
(a) 0.8
(b) 5.1
(C) 2.6
(d) 6.4
(e) 9.1
(f) 4.9
Solution:
(a) 0.8 lies between 0 and 1. From 0 to 1, 0.8 is nearer to 1
(b) 5.1 lies between 5 and 6. From 5 to 6, 5.1 is nearer to 5.
(c) 2.6 lies between 2 and 3. From 2 to 3, 2.6 is nearer to 3.
(d) 6.4 lies between 6 and 7. From 6 to 7, 6.4 is nearer to 6.
(e) 9.1 lies between 9 and 10. From 9 to 10, 9.1 is nearer to 9.
(f) 4.9 lies between 4 and 5. From 4 to 5, 4.9 is nearer to 5.

Question 8.
Show the following numbers on the number line.
(a) 0.2
(b) 1.9
(c) 1.1
(d) 2.5
Solution:

Question 9.
Write the decimal number represented by the points A, B, C, D on the given number line.

Solution:

Question 10.
(a) The length of Ramesh’s notebook is 9 cm 5 mm. What will be its length in cm?
(b) The length of a young gram plant is 65 mm. Express its length in cm.
Solution:
(a) 9 cm 5 mm = 9 cm + 5 mm
= \(\left(9+\frac{5}{10}\right)\) cm = 9.5 cm

(b) 65 mm = \(\frac{65}{10}\) cm = 6.5 cm

MP Board Class 6th Maths Solutions

MP Board Class 6th Maths Solutions Chapter 10 Mensuration Ex 10.3

Question 1.
Find the areas of the rectangles whose sides are:
(a) 3 cm and 4 cm
(b) 12 m and 21m
(c) 2 km and 3 km
(d) 2 m and 70 cm
Solution:
(a) Area of rectangle = length × breadth
= 3 cm × 4 cm = 12 cm²

(b) Area of rectangle = length × breadth
= 12 m × 21 m = 252 m²

(c) Area of rectangle = length × breadth
= 2 km × 3 km = 6 km²

(d) Area of rectangle = length × breadth
= 2 m × 70 cm = 2 m × 0.7 m = 1.4 m²

Question 2.
Find the areas of the squares whose sides are:
(a) 10 cm
(b) 14 cm
(c) 5 m
Solution:
(a) Area of square = side × side
= 10 cm × 10 cm = 100 cm²

(b) Area of square = side × side
= 14 cm × 14 cm = 196 cm²

(c) Area of square = side × side
= 5 m × 5 m = 25 m²

Question 3.
The length and breadth of three rectangles are as given below:
(a) 9 m and 6 m
(b) 17 m and 3 m
(c) 4 m and 14 m
Which one has the largest area and which one has the smallest?
Solution:
(a) Area of rectangle = length × breadth
= 9m × 6m = 54m²

(b) Area of rectangle = length × breadth
= 17 m × 3 m = 51 m²

(c) Area of rectangle = length × breadth
= 4 m × 14 m = 56 m²
Thus, rectangle (c) has the largest area, i.e. 56 m² and rectangle (b) has the smallest area, i.e., 51 m².

Question 4.
The area of a rectangular garden 50 m long is 300 sq m. Find the width of the garden.
SolutionL
Length of rectangle = 50 m
Area of rectangle = 300 m²
Since, area of rectangle = length × breadth
Therefore, breadth = \(\frac{\text { area of rectangle }}{\text { length }}\)
= \(\frac{300}{50}\) m = 6 m
Thus, the breadth of the garden is 6 m.

Question 5.
What is the cost of tiling a rectangular plot of land 500 m long and 200 m wide at the rate of Rs. 8 per hundred sq m?
Solution:
Length of land = 500 m
Breadth of land = 200 m
Area of land = length × breadth
= 500 m × 200 m = 1,00,000 sq m
Cost of tiling 100 sq m of land = Rs. 8
∴ Cost of tiling 1,00,000 sq m of land
= Rs. \(\frac{8 \times 100000}{100}\) = Rs. 8000

Question 6.
A table-top measures 2 m by 1 m 50 cm. What is its area in square metres?
Solution:
Length of table-top = 2 m
Breadth of table-top = 1 m 50 cm = 1.50 m
∴ Area of table-top = length × breadth
= 2 m × 1.50 m = 3 m²

Question 7.
A room is 4 m long and 3 m 50 cm wide. How many square metres of carpet is needed to cover the floor of the room?
Solution:
Length of room = 4 m
And breadth of room = 3 m 50 cm = 3.50 m
∴ Area of carpet = length × breadth
= 4 m × 3.50 m = 14 m²

Question 8.
A floor is 5 m long and 4 m wide. A square carpet of sides 3 m is laid on the floor. Find the area of the floor that is not carpeted.
Solution:
Length of floor = 5 m
And breadth of floor = 4 m
Area of floor = length × breadth
= 5m × 4m = 20m²
Now, side of square carpet = 3 m
Area of square carpet = side × side
= 3m × 3m = 9m²
∴ Area of floor that is not carpeted
= 20 m² – 9 m² = 11 m²

Question 9.
Five square flower beds each of sides 1 m are dug on a piece of land 5 m long and 4 m wide. What is the area of the remaining part of the land?
Solution:
Side of square flower bed = 1 m Area of square flower bed = side × side
= 1m × 1m = 1m²
∴ Area of 5 square flower beds = (1 × 5) m²
= 5 m²
Now, length of land = 5 m
And breadth of land = 4 m
∴ Area of land = length × breadth = 5m × 4m
= 20 m²
∴ Area of remaining part
= Area of land – Area of 5 flower beds
= 20 m² – 5 m² = 15 m²

Question 10.
By splitting the following figures into rectangles, find their areas (The measures are given in centimeters).

Solution:
(a) We have,

Area of square HKLM = 3 × 3 cm² = 9 cm²
Area of rectangle I]CH = 1 × 2 cm² = 2 cm²
Area of square FEDG = 3 × 3 cm² = 9 cm²
Area of rectangle ABCD = 2 × 4 cm² = 8 cm²
∴ Total area of the figure = (9 + 2 + 9 + 8) cm² = 28 cm²

(b) We have,

Area of rectangle ABCD = 3 × 1 cm² = 3 cm²
Area of rectangle BJEF = 3 × 1 cm² = 3 cm²
Area of rectangle FGHI = 3 × 1 cm² = 3 cm²
∴ Total area of the figure = (3 + 3 + 3) cm² = 9 cm²

Question 11.
Split the following shapes into rectangles and find their areas. (The measures are given in centimetres).

Solution:
(a) We have,

Area of rectangle ABCD = 2 × 10 cm² = 20 cm²
Area of rectangle DEFG = 10 × 2 cm² = 20 cm²
∴ Total area of the figure = (20 + 20) cm²
= 40 cm²

(b) We have,

There are 5 squares each of side 7 cm.
Area of one square = 7 × 7 cm² = 49 cm²
∴ Area of 5 squares = 5 × 49 cm² = 245 cm²

(c) We have,

Area of rectangle ABCD = 5 × 1 cm² = 5 cm²
Area of rectangle EFGH = 4 × 1 cm² = 4 cm²
∴ Total area of the figure = (5 + 4) cm²
= 9 cm²

Question 12.
How many tiles whose length and breadth are 12 cm and 5 cm respectively will be needed to fit in a rectangular region whose length and breadth are respectively:
(a) 100 cm and 144 cm
(b) 70 cm and 36 cm.
Solution:
(a) Area of rectangular region
= length × breadth = 100 cm × 144 cm = 14400 cm²
Area of one tile = 12 cm × 5 cm = 60 cm²

Thus, 240 tiles are required.

(b) Area of rectangular region
= length × breadth = 70 cm × 36 cm = 2520 cm²
Area of one tile = 12 cm × 5 cm = 60 cm²
∴ Number of tiles
= \(\frac{\text { Area of rectangular region }}{\text { Area of one tile }}=\frac{2520}{60}\) = 40
Thus, 42 tiles are required.

MP Board Class 6th Maths Solutions

MP Board Class 6th Maths Solutions Chapter 9 Data Handling Ex 9.2

Question 1.
Total number of animals in five villages are as follows:
Village A : 80 Village B : 120
Village C : 90 Village D : 40
Village E : 60
Prepare a pictograph of these animals using one symbol to represent 10 animals and answer the following questions :
(a) How many symbols represent animals of village E?
(b) Which village has the maximum number of animals?
(c) Which village has more animals : village A or village C?
Solution:

(a) 6 symbols represent animals of village E.
(b) Village B has the maximum number of animals.
(c) Village C has more animals than village A.

Question 2.
Total number of students of a school in different years is shown in the following table.

A. Prepare a pictograph of students using one symbol img 2 to represent 100 students and answer the following questions:
(a) How many symbols represent total number of students in the year 2002?
(b) How many symbols represent total number of students for the year 1998?
B. Prepare another pictograph of students using any other symbol each representing 50 students. Which pictograph do you find more informative?
Solution:
A.

(a) 6 symbols represent total number of students in the year 2002.
(b) Five completed and one incomplete symbols represent total number of students for the year 1998.
B.

Pictograph B is more informative than pictograph A.

MP Board Class 6th Maths Solutions

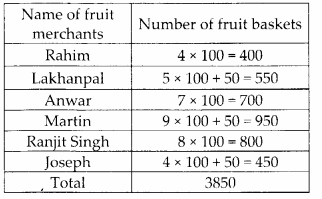
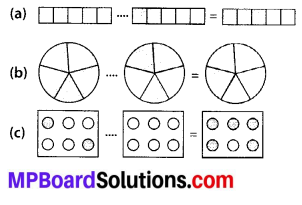
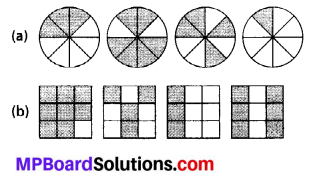
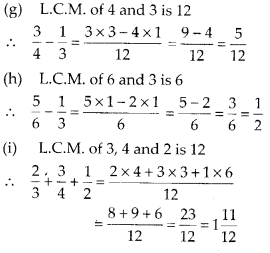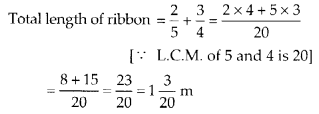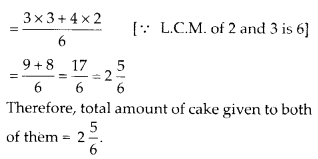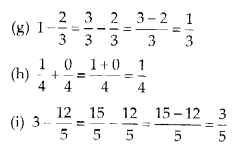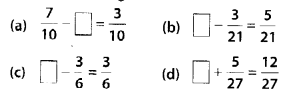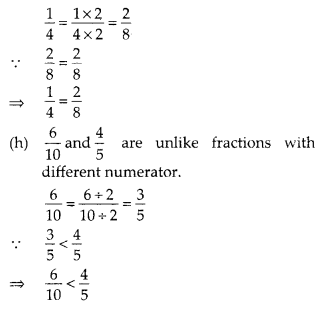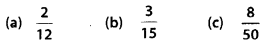MP Board Class 6th Maths Solutions Chapter 10 Mensuration Ex 10.2

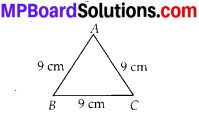
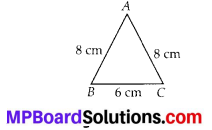
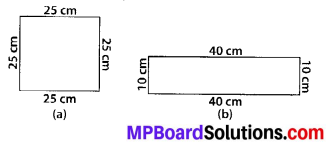
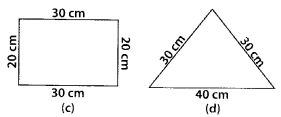
Question 1.
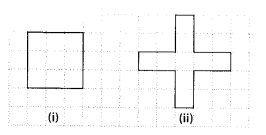
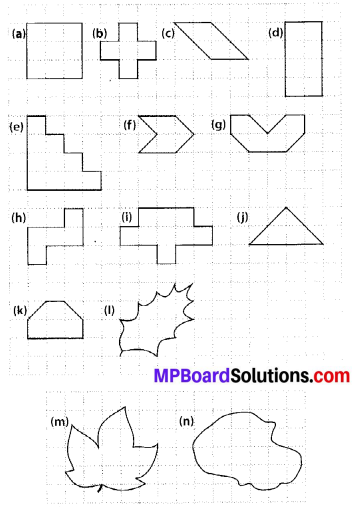
Find the areas of the following figures by counting square:

Solution:
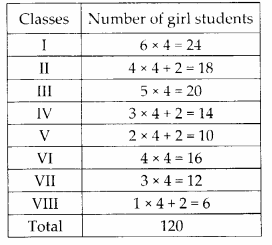
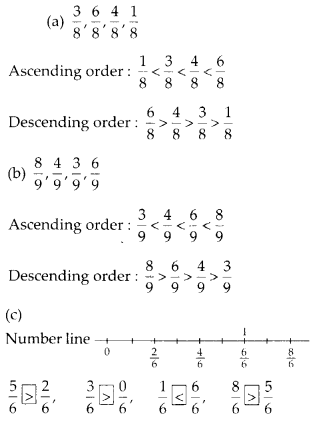
(a) Number of filled squares = 9
∴ Area covered by filled squares
= (9 × 1) sq units = 9 sq units

(b) Number of filled squares = 5
∴ Area covered by filled squares
= (5 × 1) sq units = 5 sq units

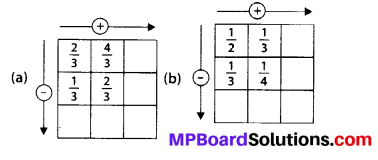
(c) Number of fully-filled squares = 2
Number of half-filled squares = 4
∴ Area covered by fully-filled squares
= (2 × 1) sq units = 2 sq units
Area covered by half-filled squares
= (4 × \(\frac{1}{2}\)) sq units = 2 sq units
∴ Total area = (2 + 2) sq units = 4 sq units

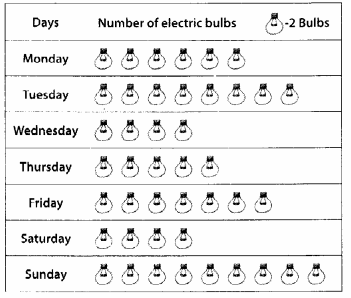
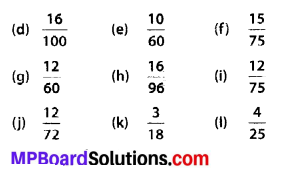
(d) Number of filled squares = 8
∴ Area covered by filled squares
= (8 × 1) sq units = 8 sq units

(e) Number of filled squares = 10
∴ Area covered by filled squares
= (10 × 1) sq units = 10 sq units

(f) Number of fully-filled squares = 2
Number of half-filled squares = 4
∴ Area covered by fully-filled squares
= (2 × 1) sq units = 2 sq units
Area covered by half-filled squares
= (4 × \(\frac{1}{2}\)) sq units = 2 sq units
∴ Total area = (2 + 2) sq units = 4 sq units

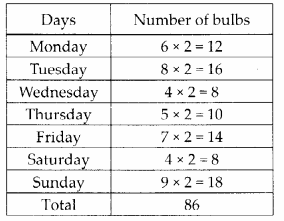
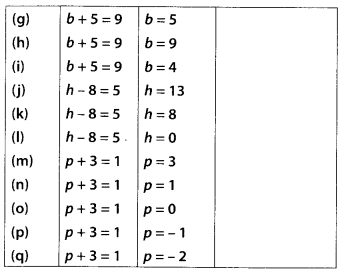
(g) Number of fully-filled squares = 4
Number of half-filled squares = 4
∴ Area covered by fully-filled squares
= (4 × 1) sq units = 4 sq units
Area covered by half-filled squares
= (4 × \(\frac{1}{2}\)) sq units = 2 sq units
∴ Total area = (4 + 2) sq units = 6 sq units

(h) Number of filled squares = 5 .
∴ Area covered by filled squares
= (5 × 1) sq units = 5 sq units

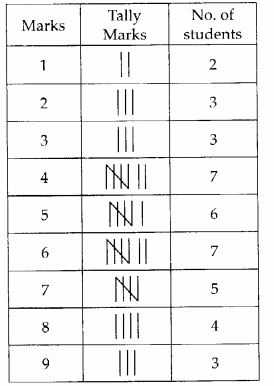
(i) Number of filled squares = 9
∴ Area covered by filled squares
= (9 × 1) sq units = 9 sq units

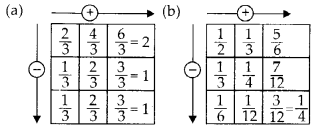
(j) Number of fully-filled squares = 2
Number of half-filled squares = 4
∴ Area covered by fully-filled squares
= (2 × 1) sq units = 2 sq units
Area covered by half-filled squares
= (4 × \(\frac{1}{2}\)) sq units = 2 sq units
∴ Total area = (2 + 2) sq units = 4 sq units

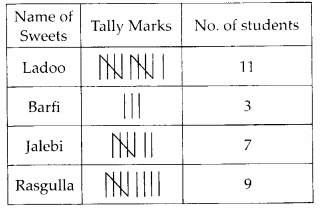
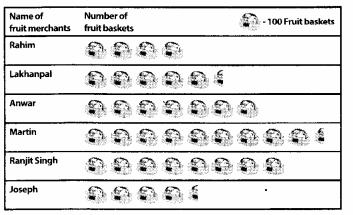
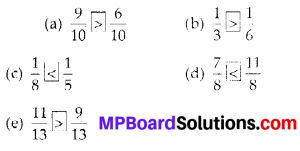
(k) Number of fully-filled squares = 4
Number of half-filled squares = 2
∴ Area covered by fully-filled squares
= (4 × 1) sq units = 4 sq units
Area covered by half-filled squares
= (2 × \(\frac{1}{2}\)) sq units = 1 sq units
∴ Total area = (4 + 1) sq units = 5 sq units

(l) Number of fully-filled squares = 3,
Number of half-filled squares = 2,
Number of more than half-filled squares = 4
and number of less than half-filled squares = 4.
Now, estimated area covered by
fully-filled squares = 3 sq units,
half-filled squares = (2 × \(\frac{1}{2}\)) sq units
= 1 sq unit,
more than half-filled squares = 4 sq units
and less than half-filled squares
= 0 sq unit
∴ Total area = (3 + 1 + 4 + 0) sq units
= 8 sq units.

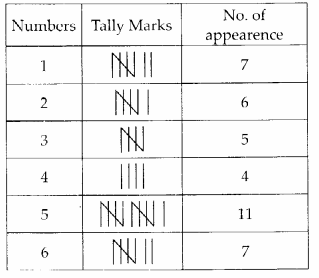
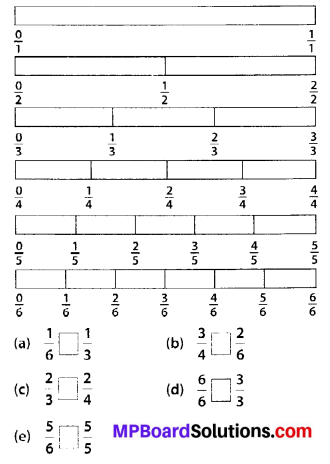
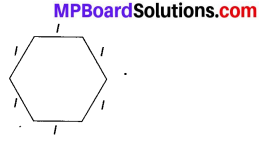
(m) Number of fully-filled squares = 7,
Number of more than half-filled squares = 7
and number of less than half-filled squares = 5
Estimated area covered by
fully-filled squares = 7 sq units,
more than half-filled squares = 7 sq units
and less than half-filled squares = 0 sq unit
∴ Total area = (7 + 7 + 0) sq units = 14 sq units

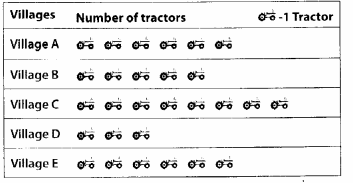
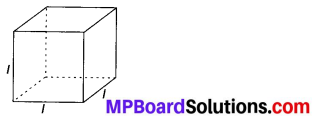
(n) Number of fully-filled squares = 10,
Number of more than half-filled squares = 8
and number of less than half-filled squares = 5
Estimated area covered by
fully-filled squares = 10 sq units,
more than half-filled squares = 8 sq units
less than half-filled squares = 0 sq unit
∴ Total area = (10 + 8 + 0) sq units
= 18 sq units.

MP Board Class 6th Maths Solutions

MP Board Class 6th Maths Solutions Chapter 9 Data Handling Ex 9.1

Question 1.
In a Mathematics test, the following marks were obtained by 40 students. Arrange these marks in a table using tally marks.

(a) Find how many students obtained marks equal to or more than 7.
(b) How many students obtained marks
Solution:

(a) 5 + 4 + 3 = 12 students obtained marks equal to or more than 7.
(b) 2 + 3 + 3 = 8 students obtained marks below 4.

Question 2.
Following is the choice of sweets of 30 students of Class VI.
Ladoo, Barfi, Ladoo, Jalebi, Ladoo, Rasgulla, Jalebi, Ladoo, Barfi, Rasgulla, Ladoo, Jalebi, Jalebi, Rasgulla, Ladoo, Rasgulla, Jalebi, Ladoo, Rasgulla, Ladoo, Ladoo, Barfi, Rasgulla, Rasgulla, Jalebi, Rasgulla, Ladoo, Rasgulla, Jalebi, Ladoo.
(a) Arrange the names of sweets in a table using tally marks.
(b) Which sweet is preferred by most of the students?
Solution:

(b) Ladoo is preferred by most of the students.

Question 3.
Catherine threw a dice 40 times and noted the number appearing each time as shown below:

Make a table and enter the data using tally marks. Find the number that appeared
(a) The minimum number of times.
(b) The maximum number of times.
(c) Find those numbers that appear an equal number of times
Solution:

(a) 4 appeared minimum number of times.
(b) 5 appeared maximum number of times.
(c) 1 and 6 appeared equal number of times.

Question 4.
Following pictograph shows the number of tractors in five villages.

Observe the pictograph and answer the following questions.
(i) Which village has the minimum number of tractors?
(ii) Which village has the maximum number of tractors?
(iii) Flow many more tractors village C has as compared to village B.
(iv) What is the total number of tractors in all the five villages?
Solution:
(i) Village D has the minimum number of tractors.
(ii) Village C has the maximum number of tractors.
(iii) Village C has 8 – 5 = 3 more tractors than village B.
(iv) Total number of tractors = 6 + 5 + 8 + 3 + 6 = 28

Question 5.
The number of girl students in each class of a co-educational middle school is depicted by the pictograph:

Observe this pictograph and answer the following questions:
(a) Which class has the minimum number of girl students?
(b) Is the number of girls in Class VI less than the number of girls in Class V?
(c) Flow many girls are there in Class VII?
Solution:

(a) Class VIII has the minimum number of girl students.
(b) No, the number of girls in Class VI is greater than the number of girls in Class V.
(c) There are 12 girls in Class VII.

Question 6.
The sale of electric bulbs on different days of a week is shown below:

Observe the pictograph and answer the following questions:
(a) How many bulbs were sold on Friday?
(b) On which day were the maximum number of bulbs sold?
(c) On which of the days same number of bulbs were sold?
(d) On which of the days minimum number of bulbs were sold?
(e) If one big carton can hold 9 bulbs. How many cartons were needed in the given week ?
Solution:

(a) Number of bulbs sold on Friday is 14.
(b) Maximum number of bulbs were sold on Sunday.
(c) Same number of bulbs were sold on Wednesday and Saturday.
(d) Minimum number of bulbs were sold on Wednesday and Saturday.
(e) The total number of bulbs were sold in the given week = 86
Number of cartons required for 9 bulbs = 1
∴ Number of cartons required for 86 bulbs = 86 ÷ 9 = 9.55 = 10
Therefore, 10 cartons were needed in the given week.

Question 7.
In a village six fruit merchants sold the following number of fruit baskets in a particular season:

Observe this pictograph and answer the following questions:
(a) Which merchant sold the maximum number of baskets?
(b) How many fruit baskets were sold by Anwar?
(c) The merchants who have sold 600 or more number of baskets are planning to buy a godown for the next season. Can you name them?
Solution:

(a) Martin sold the maximum number of baskets.
(b) 700 fruit baskets were sold by Anwar.
(c) Anwar, Martin and Ranjit Singh have sold more than 600 baskets.

MP Board Class 6th Maths Solutions