MP Board Class 8th Maths Solutions Chapter 2 Linear Equations in One Variable Ex 2.2
Question 1.
If you subtract \(\frac{1}{2}\) from a number and multiply the result by \(\frac{1}{2}\), you get \(\frac{1}{8}\).What is the number?
Solution:
Let the number be x.

Question 2.
The perimeter of a rectangular swimming pool is 154 m. Its length is 2 m more than twice its breadth. What is the length and the breadth of the pool?
Solution:
Assume that the breadth of the rectangular pool be x m.
∴ Length = 2 + 2x
Perimeter of the rectangular pool = 2(Length + Breadth)
⇒ 154 = 2(2 + 2x + x)
⇒ 154 = 2(2 + 3x)
⇒ 154 = 4 + 6x
Transposing 4 to L.H.S., we get
154 – 4 = 6x ⇒ 150 = 6x
Now, dividing both sides by 6, we get
![]()
∴ The breadth of the pool is 25 m and length of the pool = (2 + 2 × 25) m = (2 + 50) m = 52 m.
Question 3.
The base of an isosceles triangle is \(\frac{4}{3}\) cm. The perimeter of the triangle is 4\frac{2}{15} cm. What is the length of either of the remaining equal sides?
Solution:
The base of an isosceles triangle = \(\frac{4}{3}\) cm
Let x cm be the length of both of the remaining equal sides of the isosceles triangle.
Perimeter of the isosceles ∆ABC = AB + BC + CA
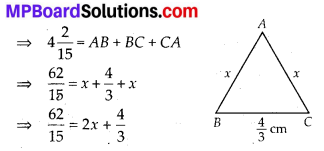
Transposing \(\frac{4}{3}\) to L.H.S., we get
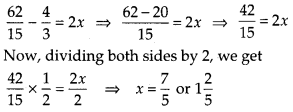
∴ The length of either of the remaining equal sides is 1\(\frac{2}{5}\) cm.
![]()
Question 4.
Sum of two numbers is 95. If one exceeds the other by 15, find the numbers.
Solution:
Let one number be x and other number is 15 + x.
Now, x + 15 + x = 95 ⇒ 2x + 15 = 95
Transposing 15 to R.H.S., we get
2x = 95 – 15 ⇒ 2x = 80
Now, dividing both sides by 2, we get
![]()
∴ One number is 40 and other number is 15 + 40 = 55.
Question 5.
Two numbers are in the ratio 5 : 3. If they differ by 18, what are the numbers?
Solution:
Since, two numbers are in the ratio 5 : 3.
Let the two numbers be 5x and 3x.
Now, 5x – 3x = 18 ⇒ 2x = 18
Dividing both sides by 2, we get
![]()
⇒ x = 9
∴ The required numbers are 5x = 5 × 9 = 45 and 3x = 3 × 9 = 27.
![]()
Question 6.
Three consecutive integers add up to 51. What are these integers?
Solution:
Let three consecutive integers be x, (x + 1) and (x + 2).
Now, x+x + 1+ x + 2 = 51 ⇒ 3x + 3 = 51
Transposing 3 to R.H.S., we get
3x = 51 – 3
⇒ 3x = 48
Dividing both sides by 3, we get
![]()
Thus, the required three consecutive integers are 16,17 and 18.
![]()
Question 7.
The sum of three consecutive multiples of 8 is 888. Find the multiples.
Solution:
Let the three consecutive multiples of 8 be 8x, 8(x + 1) and 8(x + 2).
Now, 8x + 8x + 8 + 8x + 16 = 888
⇒ 24x + 24 = 888
Transposing 24 to R.H.S., we get
24x = 888 – 24 ⇒ 24x = 864
Dividing both sides by 24, we get

Thus, the required three consecutive multiples of 8 are 8 × 36 = 288, 8 × 37 = 296 and 8 × 38 = 304.
Question 8.
Three consecutive integers are such that when they are taken in increasing order and multiplied by 2, 3 and 4 respectively, they add up to 74. Find these numbers.
Solution:
Let three consecutive integers be x, (x + 1) and (x + 2).
When they are multiplied by 2, 3 and 4, we get 2x, 3(x +1) and 4(x + 2) i.e., 2x, (3x + 3) and (4x + 8) respectively.
Now, 2x + 3x + 3 + 4x + 8 = 74 × 9x + 11 = 74
Transposing 11 to R.H.S., we get
9x = 74 – 11 ⇒ 9x = 63
Now, dividing both sides by 9, we get
![]()
Thus, the required three consecutive integers are 7, 8 and 9.
![]()
Question 9.
The ages of Rahul and Haroon are in the ratio 5 : 7. Four years later the sum of their ages will be 56 years. What are their present ages?
Solution:
Since, the ages of Rahul and Haroon are in the ratio 5 : 7.
Let Rahul’s present age be 5x years and Haroon’s present age be 7x years.
After 4 years, we have
Rahul’s age = 5x + 4 and Haroon’s age = 7x + 4
Now, 5x + 4 + 7x + 4 = 56 ⇒ 12x + 8 = 56
Transposing 8 to R.H.S., we get
12x = 56 – 8 ⇒ 12x = 48
Now, dividing both sides by 12, we get
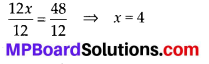
Thus, Rahul’s present age = 5 × 4 = 20 years and Haroon’s present age = 7 × 4 = 28 years
Question 10.
The number of boys and girls in a class are in the ratio 7 : 5. The number of boys is 8 more than the number of girls. What is the total class strength?
Solution:
We know that the number of boys and girls are in ratio 7 : 5.
Let the number of boys be 7x and the number of girls be 5x.
Now, 7x = 5x + 8
Transposing 5x to L.H.S., we get
7x – 5x = 8 ⇒ 2x = 8
Dividing both sides by 2, we get
![]()
Thus, the required number of boys = 7 × 4 = 28 and the required number of girls = 5 × 4 = 20
Hence, total number of students = 28 + 20 = 48
![]()
Question 11.
Baichung’s father is 26 years younger than Baichung’s grandfather and 29 years older than Baichung. The sum of the ages of all the three is 135 years. What is the age of each one of them?
Solution:
Let Baichung’s grandfather’s age be x years.
∴ Baichung’s father’s age = (x – 26) years
Baichung’s age = [(x – 26) – 29] years = (x – 55) years
Since, sum of the ages of all the three is 135 years. So, x + x – 26 + x – 55 = 135
⇒ 3x – 81 = 135
Transposing – 81 to R.H.S., we get
3x = 135 + 81 ⇒ 3x = 216
Dividing both sides by 3, we get
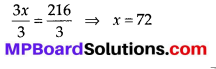
Thus, Baichung’s grandfather’s age = 72 years
Baichung’s father’s age = (72 – 26) years = 46 years
Baichung’s age = (72 – 55) years = 17 years
![]()
Question 12.
Fifteen years from now Ravi’s age will be four times his present age. What is Ravi’s present age?
Solution:
Let the present age of Ravi be x years.
After 15 years, Ravi’s age = (15 + x) years
Now, 15 + x = 4x
Transposing x to R.H.S., we get
15 = 4x – x
⇒ 15 = 3x
Dividing both sides by 3, we get
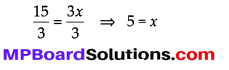
Thus, the present age of Ravi is 5 years.
Question 13.
A rational number is such that when you multiply it by \(\frac{5}{2}\) and add \(\frac{2}{3}\) to the product, you get \(-\frac{7}{12}\).What is the number?
Solution:

![]()
Question 14.
Lakshmi is a cashier in a bank. She has currency notes of denominations ₹ 100, ₹ 50 and ₹ 10, respectively. The ratio of the number of these notes is 2 : 3 : 5. The total cash with Lakshmi is ₹ 4,00,000. How many notes of each denomination does she have?
Solution:
Let the number of notes of ₹ 100, ₹ 50 and ₹ 10 be 2x, 3x and 5x, respectively.
∴ The amount Lakshmi has from ₹ 100 notes : ₹ (2x × 100) = ₹ 200x from ₹ 50 notes : ₹ (3x × 50) = ₹ 150x from ₹ 10 notes : ₹ (5x × 10) = ₹ 50x Now, 200x + 150x + 50x = 4,00,000
⇒ 400x = 4,00,000 ⇒ x = 1000
∴ Number of notes of ₹ 100 = 2x
= 2 × 1000 = 2000
Number of notes of ₹ 50 = 3x = 3 × 1000 = 3000
and number of notes of ₹ 10 = 5x = 5 × 1000
= 5000
![]()
Question 15.
I have a total of ₹ 300 in coins of denomination ₹ 1, ₹ 2 and ₹ 5. The number of ₹ 2 coins is 3 times the number of ₹ 5 coins. The total number of coins is 160. How many coins of each denomination are with me?
Solution:
Let the number of ₹ 5 coins be x.
Number of ₹ 2 coins = 3x and number of ₹ 1 coins = 160 – x – 3x
The total amount
from ₹ 5 coins : ₹ 5 × x = × 5x
from ₹ 2 coins : ₹ 2 × 3x = ₹ 6x
and from ₹ 1 coins : ₹ 1[160 – x – 3x]
= ₹ [160 – 4x]
Now, 5x + 6x + 160 – 4x = 300
⇒ 7x + 160 = 300
Transposing 160 to R.H.S., we get
7x = 300 – 160
⇒ 7x = 140
Dividing both sides by 7, we get
![]()
⇒ x = 20
The number of ₹ 1 coins = 160 – 20 – 3 × 20 = 160 – 20 – 60 = 80
Number of ₹ 2 coins = 3 × 20 = 60
Number of ₹ 5 coins = 20
![]()
Question 16.
The organisers of an essay competition decide that a winner in the competition gets a prize of ₹ 100 and a participant who does not win gets a prize of ₹ 25. The total prize money distributed is ₹ 3,000. Find the number of winners, if the total number of participants is 63.
Solution:
Let the number of winners be x.
Then, the number of losers will be 63 – x.
Since, the winner gets a prize of ₹ 100 and a loser gets a prize of ₹ 25.
Amount got by winners = ₹ 100x
And amount got by losers = ₹ (63 – x) × 25 But total prize money is ₹ 3000.
Therefore, 100x + (63 – x) × 25 = 3000
⇒ 100x + 63 × 25 – 25x = 3000
⇒ 75x + 1575 = 3000

So, the number of winners is 19.