Category: Class 8

MP Board Class 8th Maths Solutions Chapter 2 Linear Equations in One Variable Ex 2.3

Solve the following equations and check your results.

Question 1.
3x = 2x + 18
Solution:
We have, 3x = 2x + 18
Transposing 2x to L.H.S., we get
3x – 2x = 18 ⇒ x = 18
Checking: L.H.S. = 3 × 18 = 54
R.H.S. = 2x + 18 = 2 × 18 + 18 = 36 + 18 = 54
Thus, L.H.S. = R.H.S.

Question 2.
5t – 3 = 3t – 5
Solution:
We have, 5t – 3 = 3t – 5
Transposing 3t to L.H.S., we get
5t – 3 – 3t = – 5
⇒ 2t – 3 = – 5
Transposing – 3 to R.H.S., we get
2t = -5 + 3
⇒ 2t = – 2
Dividing both sides by 2, we get

Checking : L.H.S. = 5t – 3 = 5 × (-1) – 3 = -5 – 3 = -8
R.H.S. = 3t – 5 = 3 × (-1) – 5 = -3 – 5 = -8
Thus, L.H.S. = R.H.S.

Question 3.
5x + 9 = 5 + 3x
Solution:
We have, 5x + 9 = 5 + 3x
Transposing 3x to L.H.S., we get
5x + 9 – 3x = 5
⇒ 2x + 9 = 5
Now, transposing 9 to R.H.S., we get
2x = 5 – 9 = 4 ⇒ 2x = – 4
Dividing both sides by 2, we get \(\frac{2 x}{2}=\frac{-4}{2}\)
Checking: L.H.S. = 5x + 9 = 5 × (-2) + 9 = -10 + 9 = -1
R.H.S. = 5 + 3x = 5 + 3 (-2) = 5 – 6 = – 1.
Thus, L.H.S. = R.H.S.

Question 4.
4z + 3 = 6 + 2z
Solution:
We have, 4z + 3 = 6 + 2z
Transposing 2z to L.H.S., we get
4z + 3-2z = 6 ⇒ 2z + 3 = 6
Transposing 3 to R.H.S., we get
2z = 6 – 3 ⇒ 2z = 3

Question 5.
2x – 1 = 14 – x
Solution:
We have, 2x -1 = 14 – x
Transposing – x to L.H.S., we get
2x – 1 + x = 14 ⇒ 3x – 1 = 14
Transposing – 1 to R.H.S., we get
3x = 14 + 1 ⇒ 3x = 15
Dividing both sides by 3, we get \(\frac{3 x}{3}=\frac{15}{3}\)
⇒ x = 15
Checking: L.H.S. = 2x – 1 = 2 × 5 – 1 = 10 – 1 = 9
R.H.S. = 14 – x = 14 – 5 = 9
Thus, L.H.S. = R.H.S.

Question 6.
8x + 4 = 3(x – 1) + 7
Solution:
We have, 8x + 4 = 3(x – 1) + 7
⇒ 8x + 4 = 3x – 3 + 7 ⇒ 8x + 4 = 3x + 4
Transposing 3x to L.H.S., we get
8x + 4 – 3x = 4 ⇒ 5x + 4 = 4
Transposing 4 to R.H.S., we get
⇒ 5x = 4 – 4 ⇒ 5x = 0
Dividing both sides by 5, we get

Checking: L.H.S. = 8x + 4 = 8 × 0 + 4 = 4
R.H.S. = 3(x – 1) + 7 = 3(0 – 1) + 7 = -3 + 7 = 4
Thus, L.H.S. = R.H.S.

Question 7.
x = \(\frac{4}{5}\)(x + 10)
Solution:
We have, x = \(\frac{4}{5}\)(x + 10)
Multiplying both sides by 5, we get
5x = 4(x + 10) ⇒ 5x = 4x + 40
Transposing 4x to L.H.S., we get 5x – 4x = 40 ⇒ x = 40
Checking : L.H.S. = x = 40

Thus, L.H.S. = R.H.S.

Question 8.
\(\frac{2 x}{3}+1=\frac{7 x}{15}+3\)
Solution:

Question 9.
\(2 y+\frac{5}{3}=\frac{26}{3}-y\)
Solution:

Question 10.
3m = 5m – \(\frac{8}{5}\)
Solution:

MP Board Class 8th Maths Solutions

MP Board Class 8th Maths Solutions Chapter 2 Linear Equations in One Variable Ex 2.2

Question 1.
If you subtract \(\frac{1}{2}\) from a number and multiply the result by \(\frac{1}{2}\), you get \(\frac{1}{8}\).What is the number?
Solution:
Let the number be x.

Question 2.
The perimeter of a rectangular swimming pool is 154 m. Its length is 2 m more than twice its breadth. What is the length and the breadth of the pool?
Solution:
Assume that the breadth of the rectangular pool be x m.
∴ Length = 2 + 2x
Perimeter of the rectangular pool = 2(Length + Breadth)
⇒ 154 = 2(2 + 2x + x)
⇒ 154 = 2(2 + 3x)
⇒ 154 = 4 + 6x
Transposing 4 to L.H.S., we get
154 – 4 = 6x ⇒ 150 = 6x
Now, dividing both sides by 6, we get

∴ The breadth of the pool is 25 m and length of the pool = (2 + 2 × 25) m = (2 + 50) m = 52 m.

Question 3.
The base of an isosceles triangle is \(\frac{4}{3}\) cm. The perimeter of the triangle is 4\frac{2}{15} cm. What is the length of either of the remaining equal sides?
Solution:
The base of an isosceles triangle = \(\frac{4}{3}\) cm
Let x cm be the length of both of the remaining equal sides of the isosceles triangle.
Perimeter of the isosceles ∆ABC = AB + BC + CA

Transposing \(\frac{4}{3}\) to L.H.S., we get

∴ The length of either of the remaining equal sides is 1\(\frac{2}{5}\) cm.

Question 4.
Sum of two numbers is 95. If one exceeds the other by 15, find the numbers.
Solution:
Let one number be x and other number is 15 + x.
Now, x + 15 + x = 95 ⇒ 2x + 15 = 95
Transposing 15 to R.H.S., we get
2x = 95 – 15 ⇒ 2x = 80
Now, dividing both sides by 2, we get

∴ One number is 40 and other number is 15 + 40 = 55.

Question 5.
Two numbers are in the ratio 5 : 3. If they differ by 18, what are the numbers?
Solution:
Since, two numbers are in the ratio 5 : 3.
Let the two numbers be 5x and 3x.
Now, 5x – 3x = 18 ⇒ 2x = 18
Dividing both sides by 2, we get

⇒ x = 9
∴ The required numbers are 5x = 5 × 9 = 45 and 3x = 3 × 9 = 27.

Question 6.
Three consecutive integers add up to 51. What are these integers?
Solution:
Let three consecutive integers be x, (x + 1) and (x + 2).
Now, x+x + 1+ x + 2 = 51 ⇒ 3x + 3 = 51
Transposing 3 to R.H.S., we get
3x = 51 – 3
⇒ 3x = 48
Dividing both sides by 3, we get

Thus, the required three consecutive integers are 16,17 and 18.

Question 7.
The sum of three consecutive multiples of 8 is 888. Find the multiples.
Solution:
Let the three consecutive multiples of 8 be 8x, 8(x + 1) and 8(x + 2).
Now, 8x + 8x + 8 + 8x + 16 = 888
⇒ 24x + 24 = 888
Transposing 24 to R.H.S., we get
24x = 888 – 24 ⇒ 24x = 864
Dividing both sides by 24, we get

Thus, the required three consecutive multiples of 8 are 8 × 36 = 288, 8 × 37 = 296 and 8 × 38 = 304.

Question 8.
Three consecutive integers are such that when they are taken in increasing order and multiplied by 2, 3 and 4 respectively, they add up to 74. Find these numbers.
Solution:
Let three consecutive integers be x, (x + 1) and (x + 2).
When they are multiplied by 2, 3 and 4, we get 2x, 3(x +1) and 4(x + 2) i.e., 2x, (3x + 3) and (4x + 8) respectively.
Now, 2x + 3x + 3 + 4x + 8 = 74 × 9x + 11 = 74
Transposing 11 to R.H.S., we get
9x = 74 – 11 ⇒ 9x = 63
Now, dividing both sides by 9, we get

Thus, the required three consecutive integers are 7, 8 and 9.

Question 9.
The ages of Rahul and Haroon are in the ratio 5 : 7. Four years later the sum of their ages will be 56 years. What are their present ages?
Solution:
Since, the ages of Rahul and Haroon are in the ratio 5 : 7.
Let Rahul’s present age be 5x years and Haroon’s present age be 7x years.
After 4 years, we have
Rahul’s age = 5x + 4 and Haroon’s age = 7x + 4
Now, 5x + 4 + 7x + 4 = 56 ⇒ 12x + 8 = 56
Transposing 8 to R.H.S., we get
12x = 56 – 8 ⇒ 12x = 48
Now, dividing both sides by 12, we get

Thus, Rahul’s present age = 5 × 4 = 20 years and Haroon’s present age = 7 × 4 = 28 years

Question 10.
The number of boys and girls in a class are in the ratio 7 : 5. The number of boys is 8 more than the number of girls. What is the total class strength?
Solution:
We know that the number of boys and girls are in ratio 7 : 5.
Let the number of boys be 7x and the number of girls be 5x.
Now, 7x = 5x + 8
Transposing 5x to L.H.S., we get
7x – 5x = 8 ⇒ 2x = 8
Dividing both sides by 2, we get

Thus, the required number of boys = 7 × 4 = 28 and the required number of girls = 5 × 4 = 20
Hence, total number of students = 28 + 20 = 48

Question 11.
Baichung’s father is 26 years younger than Baichung’s grandfather and 29 years older than Baichung. The sum of the ages of all the three is 135 years. What is the age of each one of them?
Solution:
Let Baichung’s grandfather’s age be x years.
∴ Baichung’s father’s age = (x – 26) years
Baichung’s age = [(x – 26) – 29] years = (x – 55) years
Since, sum of the ages of all the three is 135 years. So, x + x – 26 + x – 55 = 135
⇒ 3x – 81 = 135
Transposing – 81 to R.H.S., we get
3x = 135 + 81 ⇒ 3x = 216
Dividing both sides by 3, we get

Thus, Baichung’s grandfather’s age = 72 years
Baichung’s father’s age = (72 – 26) years = 46 years
Baichung’s age = (72 – 55) years = 17 years

Question 12.
Fifteen years from now Ravi’s age will be four times his present age. What is Ravi’s present age?
Solution:
Let the present age of Ravi be x years.
After 15 years, Ravi’s age = (15 + x) years
Now, 15 + x = 4x
Transposing x to R.H.S., we get
15 = 4x – x
⇒ 15 = 3x
Dividing both sides by 3, we get

Thus, the present age of Ravi is 5 years.

Question 13.
A rational number is such that when you multiply it by \(\frac{5}{2}\) and add \(\frac{2}{3}\) to the product, you get \(-\frac{7}{12}\).What is the number?
Solution:

Question 14.
Lakshmi is a cashier in a bank. She has currency notes of denominations ₹ 100, ₹ 50 and ₹ 10, respectively. The ratio of the number of these notes is 2 : 3 : 5. The total cash with Lakshmi is ₹ 4,00,000. How many notes of each denomination does she have?
Solution:
Let the number of notes of ₹ 100, ₹ 50 and ₹ 10 be 2x, 3x and 5x, respectively.
∴ The amount Lakshmi has from ₹ 100 notes : ₹ (2x × 100) = ₹ 200x from ₹ 50 notes : ₹ (3x × 50) = ₹ 150x from ₹ 10 notes : ₹ (5x × 10) = ₹ 50x Now, 200x + 150x + 50x = 4,00,000
⇒ 400x = 4,00,000 ⇒ x = 1000
∴ Number of notes of ₹ 100 = 2x
= 2 × 1000 = 2000
Number of notes of ₹ 50 = 3x = 3 × 1000 = 3000
and number of notes of ₹ 10 = 5x = 5 × 1000
= 5000

Question 15.
I have a total of ₹ 300 in coins of denomination ₹ 1, ₹ 2 and ₹ 5. The number of ₹ 2 coins is 3 times the number of ₹ 5 coins. The total number of coins is 160. How many coins of each denomination are with me?
Solution:
Let the number of ₹ 5 coins be x.
Number of ₹ 2 coins = 3x and number of ₹ 1 coins = 160 – x – 3x
The total amount
from ₹ 5 coins : ₹ 5 × x = × 5x
from ₹ 2 coins : ₹ 2 × 3x = ₹ 6x
and from ₹ 1 coins : ₹ 1[160 – x – 3x]
= ₹ [160 – 4x]
Now, 5x + 6x + 160 – 4x = 300
⇒ 7x + 160 = 300
Transposing 160 to R.H.S., we get
7x = 300 – 160
⇒ 7x = 140
Dividing both sides by 7, we get

⇒ x = 20
The number of ₹ 1 coins = 160 – 20 – 3 × 20 = 160 – 20 – 60 = 80
Number of ₹ 2 coins = 3 × 20 = 60
Number of ₹ 5 coins = 20

Question 16.
The organisers of an essay competition decide that a winner in the competition gets a prize of ₹ 100 and a participant who does not win gets a prize of ₹ 25. The total prize money distributed is ₹ 3,000. Find the number of winners, if the total number of participants is 63.
Solution:
Let the number of winners be x.
Then, the number of losers will be 63 – x.
Since, the winner gets a prize of ₹ 100 and a loser gets a prize of ₹ 25.
Amount got by winners = ₹ 100x
And amount got by losers = ₹ (63 – x) × 25 But total prize money is ₹ 3000.
Therefore, 100x + (63 – x) × 25 = 3000
⇒ 100x + 63 × 25 – 25x = 3000
⇒ 75x + 1575 = 3000

So, the number of winners is 19.

MP Board Class 8th Maths Solutions

MP Board Class 8th Maths Solutions Chapter 2 Linear Equations in One Variable Ex 2.1

Solve the following equations.

Question 1.
x – 2 = 7.
Solution:
We have, x – 2 = 7
Transposing -2 to R.H.S., we get
x = 7 + 2 ⇒ x = 9, which is the required solution.

Question 2.
y + 3 = 10.
Solution:
We have, y + 3 = 10
Transposing 3 to R.H.S., we get y = 10 – 3
⇒ y = 7, which is the required solution.

Question 3.
6 = z + 2.
Solution:
We have, 6 = z + 2
Transposing 2 to L.H.S., we get
6 – 2 = z
⇒ z = 4, which is the required solution.

Question 4.
\(\frac{3}{7}\) + x = \(\frac{17}{7}\).
Solution:

⇒ x = 2, which is the required solution.

Question 5.
6x = 12.
Solution:
We have, 6x = 12
Dividing both sides by 6, we get
\(\frac{6 x}{6}=\frac{12}{6}\)
⇒ x = 2, which is the required solution.

Question 6.
\(\frac{t}{5}=10\)
Solution:
We have, \(\frac{t}{5}\) = 10
Multiplying both sides by 5, we get

⇒ t = 50, which is the required solution.

Question 7.
\(\frac{2 x}{3}\) = 18
Solution:
We have,
\(\frac{2 x}{3}\) = 18
Dividing both sides by 2, we get

Now, multiplying both sides by 3, we get

⇒ x = 27, which is the required solution.

Question 8.
\(1.6=\frac{y}{1.5}\)
Solution:
We have, \(1.6=\frac{y}{1.5}\)
Multiplying both sides by 1.5, we get

⇒ y = 2.4, which is the required solution.

Question 9.
7x – 9 = 16.
Solution:
We have, 7x – 9 = 16
Transposing -9 to R.H.S., we get
7x = 16 + 9
⇒ 7x = 25
Now, dividing both sides by 7, we get

⇒ x = \(\frac{25}{7}\), which is the required solution.

Question 10.
14y – 8 = 13.
Solution:
We have, 14y -8 = 13
Transposing -8 to R.H.S., we get
14y = 13 + 8 ⇒ 14y = 21
Now, dividing both sides by 14, we get

Question 11.
17 + 6p = 9.
Solution:
We have, 17 + 6p = 9
Transposing 17 to R.H.S., we get 6p = 9 – 17
⇒ 6p = – 8
Now, dividing both sides by 6, we get

Question 12.
\(\frac{x}{3}+1=\frac{7}{15}\)
Solution:

Now, multiplying both sides by 3, we get

⇒ x = \(-\frac{8}{5}\), which is the required solution.

MP Board Class 8th Maths Solutions

MP Board Class 8th Maths Solutions Chapter 12 घातांक और घात Ex 12.2

प्रश्न 1.
निम्न संख्याओं को मानक रूप में व्यक्त कीजिए –

1. 0.0000000000085
2. 0.00000000000942
3. 6020000000000000
4. 0.00000000837
5. 31860000000

हल:
1. 0.0000000000085 = \(\frac{85}{ 10000000000000}\)
= \(\frac { 85 }{ 10^{ 13 } } \)
= \(\frac { 8.5×10 }{ 10^{ 13 } } \) = 8.5 x 10 x 10^-13
= 8.5 x 10^-12

2. 0.00000000000942 = \(\frac{942}{ 100000000000000 }\)
= \(\frac { 942 }{ 10^{ 14 } } \)
= \(\frac { 8.42×10 }{ 10^{ 14 } } \)
= 9.42 x 10² x 10^-14
= 9.42 x 10^-12

3. 6020000000000000 = 602 x 10¹³
= 6.02 x 100 x 10¹³
= 602 x 10² x 10¹³
= 6.02 x 10¹⁵

4. 0.00000000837 = \(\frac{837 }{ 100000000000 } = \frac { 837}{ 10^{ 11 } } \)
= \(\frac { 8:37×100 }{ 10^{ 11 } } \)
= 8.37 x 10² x 10^-11
= 8.37 x 10^-9

5. 31860000000 = 3186 x 10⁷
= 3.186 x 10³ x 10⁷
= 3.186 x 10¹⁰

प्रश्न 2.
निम्न संख्याओं को सामान्य रूप में व्यक्त कीजिए –

1. 3.02 x 10^-6
2. 4.5 x 10⁴
3. 3 x 10^-8
4. 1.0001 x 10⁹
5. 5.8 x 10¹²
6. 3.61492 x 10⁶

हल:
1. 3.02 x 10^-6 = \(\frac{302}{100}\) x \(\frac { 1 }{ 10^{ 6 } } \)
= \(\frac { 302 }{ 10^{ 8 } } \)
= \(\frac{302}{100000000}\)

2. 4.5 x 10⁴ = \(\frac{45}{10}\) x 10⁴
= 45 x 10³
= 45000

3. 3 x 10^-8 = \(\frac{3}{100000000}\)
= 0.00000003

4. 1.0001 x 10⁹ = \(\frac{10001}{10000}\) x 10⁹
= 10001 x 10⁹ x 10^-4
= 10001 x 10⁵
= 1000100000

5. 5.8 x 10¹² = \(\frac{58}{10}\) x 10¹²
= 58 x 10¹² x 10^-1
= 58 x 10¹¹
= 5800000000000

6. 3.61492 x 10⁶ = \(\frac{361492}{100000}\)
= 361492 x 10⁶ x 10^-5
= 361492 x 10
= 3614920

प्रश्न 3.
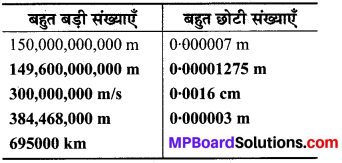
निम्नलिखित कथनों में जो संख्या प्रकट हो रही है उन्हें मानक रूप में व्यक्त कीजिए –

1. 1 माइक्रॉन \(\frac{1}{100000}\) m के बराबर होता है।
2. एक इलेक्ट्रॉन का आवेश 0.000,000,000,000,000,000,16 कूलॉम होता है।
3. जीवाणु की माप 0.0000005 m है।
4. पौधों की कोशिकाओं की माप 0.00001275 m
5. मोटे कागज की मोटाई 0.07 mm है।

हल:
1. 1 माइक्रॉन = \(\frac{1}{1000000}\)m
= 1 x 10^-6m

2. एक इलेक्ट्रॉन का आवेश = 0.000,000,000,000,000,00016
= \(\frac{16}{100000000000000000000}\)
= \(\frac { 16 }{ 10^{ 20 } } \) = \(\frac { 1.6×10 }{ 10^{ 20 } } \)
= 1.6 x 10 x 10^-20
= 1.6 x 10^-19 कूलॉम

3. एक जीवाणु की माप 0.0000005 m
= \(\frac{5}{10000000}\)
= 5 x 10^-7 m

4. पौधों की कोशिकाओं की माप 0.00001275 m
= \(\frac{1275}{100000000}\)
= \(\frac { 1.275×1000 }{ 10^{ 8 } } \)
= 1.275 x 10³ x 10^-8
= 1.275 x 10^-5 m

5. एक मोटे कागज की मोटाई 0.07 mm
= \(\frac{7}{100}\)
= 7 x 10^-2 mm

प्रश्न 4.
एक ढेर में पाँच किताबें हैं जिनमें प्रत्येक की मोटाई 20 mm तथा पाँच कागज की शीटें हैं जिनमें प्रत्येक की । मोटाई 0.016 mm है। इस ढेर की कुल मोटाई ज्ञात कीजिए।
हल:
यहाँ, 1 किताब की मोटाई = 20 mm
∴ 5 किताबों की मोटाई = 5 x 20 mm
= 100mm
∴ 1 कागज की शीट की मोटाई = 0.016 mm
∴ 5 कागज की शीटों की मोटाई = 5 x 0.016 mm
= 0.080 mm
∴ ढेर की कुल मोटाई = 5 किताबों की मोटाई + 5 कागज की शीटों की मोटाई
= 100 mm + 0.080 mm
= 10008 mm
\(\frac{1.0008×10000}{100}\)
= 1.0008 x 10⁴ x 10^-2
= 1.0008 x 10² mm

MP Board Class 8th Maths Solutions

MP Board Class 8th Maths Solutions Chapter 1 Rational Numbers Ex 1.2

Question 1.
Represent these numbers on the number line.
(i) \(\frac{7}{4}\)
(ii) \(\frac{-5}{6}\)
Solution:
(i) We have to represent \(\frac{7}{4}\) on the number line. \(\frac{7}{4}\) can be written as \(1 \frac{3}{4} \cdot 1 \frac{3}{4}\) lies between 1 and 2.
Step-1: Draw a number line and mark O on it to represents ‘0’ (zero)
Step-2 : Take a point A to represent
1 and B to represent 2.
Step-3 : Divide the distance of A and B in four equal parts A A₁, A₁A₂, A₂A₃, A₃B.
Step-4 : Count from 1 and reach to the third point A₃ and A₃ is the required point on number line.

(ii) \(\frac{-5}{6}\) is lies between 0 and -1.
Step-1: Draw a number line and mark O on it to represent ‘0’ (zero).
Step-2 : Take a point A to represent -1.
Step-3 : Divide the distance of A and O in six equal parts AO₅, O₅O₄, O₄O₃, O₃O₂, O₂O₁, O₁O.
Step-4 : Count from 0 and reach to the fifth point O₅.
O₅ is the required point.

Question 2.
Represent \(\frac{-2}{11}, \frac{-5}{11}, \frac{-9}{11}\) on the number line.
Solution:
We have to mark \(\frac{-2}{11}, \frac{-5}{11}, \frac{-9}{11}\) on the same number line.
Since \(\frac{-2}{11}, \frac{-5}{11}, \frac{-9}{11}\) all are less than 0 but greater than -1.
∴ All these lie between 0 and -1.

Thus, A, B and C are the required points.

Question 3.
Write five rational numbers which are smaller than 2.
Solution:
Five numbers less than 2 lies on the left of 2 on the number line.
∴ Five rational numbers are \(0, \frac{1}{5}, \frac{2}{5}, \frac{3}{5}, \frac{4}{5}\)

Question 4.
Find ten rational numbers between \(\frac{-2}{5}\) and \(\frac{1}{2}\).
Solution:
We have given, two rational numbers \(\frac{-2}{5}\) and \(\frac{1}{2}\).
First we make the same denominator of both rational numbers.

Now, we have to find 10 rational numbers between \(\frac{-4}{10}\) and \(\frac{5}{10}\). so we have to multiply the numerator and denominator by a number such that difference between numerators is atleast 10.

Question 5.
Find five rational numbers between

Solution:
First we make the same denominator of both rational numbers

Since, we have to find five rational numbers between \(\frac{10}{15}\) and \(\frac{12}{15}\) so we multiply the numerator and denominator by a number such that difference between the numerators is atleast 5.

∴ The five rational numbers between \(\frac{1}{4}\) and \(\frac{2}{4}\) are \(\frac{41}{60}, \frac{42}{60}, \frac{43}{60}, \frac{44}{60}, \frac{45}{60}\)

(ii) First we make the same denominator of both rational numbers.

Since, we have to find five rational numbers between and \(-\frac{9}{6}\) and \(\frac{10}{6}\), so we do not need to multiply the numerator and denominator of \(-\frac{9}{6}\) and \(\frac{10}{6}\) by any number, because we can see that the difference between the numerators is 19 > 5.
∴ Five rational numbers between \(\frac{-3}{2}\) and \(\frac{5}{3}\) are \(\frac{-8}{6}, \frac{-7}{6}, \frac{0}{6}, \frac{1}{6}, \frac{2}{6}\)

(iii) First we make the same denominator of both rational numbers.

Since we have to find five rational numbers between \(\frac{1}{4}\) and \(\frac{2}{4}\), so we multiply the numerator and denominator by a number such that difference between the numerators is atleast 5.

∴ Five rational numbers between \(\frac{1}{4}\) and \(\frac{2}{4}\) are \(\frac{9}{32}, \frac{10}{32}, \frac{11}{32}, \frac{12}{32}, \frac{13}{32}\).

Question 6.
Write five rational numbers greater than -2.
Solution:
Five rational numbers greater than -2 lies on the right side of -2 on number line.
∴ Any five rationals on the right of -2 are \(\frac{-3}{2},-1, \frac{-1}{2}, 0, \frac{1}{2}\).

Question 7.
Find ten rational numbers between \(\frac{3}{5}\) and \(\frac{3}{4}\)
Solution:
Make the common denominator.

Since we have to find ten rational numbers between \(\frac{3}{5}\) and \(\frac{3}{4}\) so, we multiply the numerator and denominator by a number such that difference between the numerators is atleast 10.

MP Board Class 8th Maths Solutions

MP Board Class 8th Maths Solutions Chapter 12 घातांक और घात Ex 12.1

प्रश्न 1.
मान ज्ञात कीजिए –

(i) 3^-2
(ii) (-4)^-2
(iii) (\(\frac{1}{2}\))^-5

हल:

प्रश्न 2.
सरल कीजिए और उत्तर को धनात्मक घातांक के रूप में व्यक्त कीजिए –

(i) (-4)⁵ + (-4)⁸9
(ii) (\(\frac { 1 }{ 2^{ 3 } } \))²
(iii) (-3)⁴ x \(\frac{5}{3}\)⁴
(iv) (3^-7 ÷ 3^-10) x 3 ^-5
(v) 2^-3 x (-7)^-3

हल:

प्रश्न 3.
मान ज्ञात कीजिए –

(i) (3⁰ + 4^-1) x 2²
(ii) (2^-1 x 4^-1) ÷ 2²
(iii) (\(\frac{1}{2}\))^-2 + (\(\frac{1}{3}\))^-2 + (\(\frac{1}{4}\))^-2
(iv) (3 ^-1 + 4^-1 + 5^-1)⁰
(v) \(\left\{\left(\frac{-2}{3}\right)^{-2}\right\}^{2}\)

हल:

प्रश्न 4.
मान ज्ञात कीजिए –

(i) \(\frac{8^{-1} \times 5^{3}}{2^{-4}}\)
(ii) (5^-1 x 2^-1) x 6^-1

हल:

प्रश्न 5.
m का मान ज्ञात कीजिए जिसके लिए 5^m ÷ 5^-3 = 5⁵.
हल:
5^m ÷ 5^-3 = 5⁵
या 5^m ÷ \(\frac { 1 }{ 5^{ 3 } } \) = 5⁵
या 5^m x 5³ = 5⁵
या 5^m+3 = 5⁵
या m + 3 = 5 (घातों की तुलना करने पर)
m = 5 – 3 = 2

प्रश्न 6.
मान ज्ञात कीजिए –

हल:

प्रश्न 7.
सरल कीजिए –

हल:

पाठ्य-पुस्तक पृष्ठ संख्या # 206

प्रश्न 1.
निम्न तथ्यों का अवलोकन कीजिए –

1. पृथ्वी से सूर्य की दूरी 149,600,000,000 m है।
2. प्रकाश का वेग 300,000,000 m/s है।
3. कक्षा VII की गणित की पुस्तक की मोटाई 20 mm है।
4. लाल रक्त कोशिकाओं का औसत व्यास 0.000007 mm.
5. मनुष्य के बाल की मोटाई की परास 0.005 cm से 0.01 cm होती है।
6. पृथ्वी से चन्द्रमा की दूरी लगभग 384,467,000 m है।
7. पौधों की कोशिकाओं का आकार 0.00001275 m है।
8. सूर्य की औसत त्रिज्या 695000 km है।
9. अन्तरिक्ष शटल में ठोस राकेट ब्रूस्टर को प्रेरित करने के लिए शटल का द्रव्यमान 503600 kg है।
10. एक कागज की मोटाई 0.0016 cm है।
11. कम्प्यूटर चिप के एक तार का व्यास 0.000003 m
12. माउण्ट एवरेस्ट की ऊँचाई 8,848 m है।

उपर्युक्त तथ्यों के आधार पर बहुत बड़ी और बहुत छोटी संख्याओं की पहचान कीजिए और संगत सारणी में लिखिए।
हल:

पाठ्य-पुस्तक पृष्ठ संख्या # 207

प्रयास कीजिए (क्रमांक 12.4)

प्रश्न 1.
निम्न संख्याओं को मानक रूप में लिखिए –

1. 0.000000564
2. 0.0000021
3. 21600000
4. 15240000

हल:
1. 0.000000564 = \(\frac{564}{1000000000}\)
= \(\frac { 5.64×100 }{ 10^{ 9 } } \) = 5.64 x 10^2-9
= 5.64 x 10^-7

2. 0.0000021 = \(\frac{21}{10000000}\) = \(\frac { 21 }{ 10^{ 7 } } \)
= \(\frac { 2.1×10 }{ 10^{ 7 } } \)
= 2.1 x 10^1-7
= 2.1 x 10^-6

3. 21600000 = 216 x 100000
= 2.16 x 100 x 100000
= 2.16 x 10⁷

4. 15240000 = 1524 x 10000
= 1.524 x 1000 x 10000
= 1.524 x 10⁷

प्रश्न 2.
दिए गए तथ्यों को मानक रूप में लिखिए।
हल:
पाठ्य-पुस्तक पृष्ठ संख्या 206 पर अंकित तथ्य हैं –
1. पृथ्वी से सूर्य की दूरी 149,600,000,000 m
= 1.49 x 102.1 x 10¹¹ m

2. प्रकाश का वेग 300,000,000 m/s
= 3 x 10⁸ m/s

3. कक्षा VII की गणित की पुस्तक की मोटाई 20 mm
= 2 x 10¹ mm

4. लाल रक्त कणिकाओं का औसत व्यास
0.000007 mm = 7 x 10^-6 mm

5. मनुष्य के बाल की मोटाई की परास 0.005 cm से
0.01 cm = 5 x 10^-3 cm से 1 x 10^-2 cm

6. पृथ्वी से चन्द्रमा की दूरी लगभग 384,467,000 m
= 3.84467 x 10⁸ m

7. पौधों की कोशिकाओं का आकार 0.00001275 m
= 1275 x 10^-5 m

8. सूर्य की औसत त्रिज्या 695000 km = 6.95 x 10⁵ km

9. अन्तरिक्ष शटल में ठोस राकेट बूस्टर को प्रेरित करने के लिए शटल का द्रव्यमान 5,03,600 kg =5-036 x 10⁵ kg

10. एक कागज की मोटाई 0-0016 cm = 1.6 x 10^-3 cm

11. कम्प्यूटर चिप के एक तार का व्यास 0.000003 m
= 3 x 10^-6 m

12. माउण्ट एवरेस्ट की ऊँचाई 8848 m = 8.848 x 10³ m

MP Board Class 8th Maths Solutions

MP Board Class 8th Maths Solutions Chapter 12 घातांक और घात Intext Questions

MP Board Class 8th Maths Chapter 12 पाठान्तर्गत प्रश्नोत्तर

पाठ्य-पुस्तक पृष्ठ संख्या # 201

भूमिका

प्रश्न 1.
2^-2 किसके बराबर है?
हल:
2^-2 = \(\frac { 1 }{ 2^{ 2 } } \) = \(\frac{1}{4}\)

ऋणात्मक घातांकों की घात

प्रश्न 1.
10^-10 किसके बराबर है?
हल:
∴ a^-m = \(\frac { 1 }{ a^{ m } } \)
10^-10 = \(\frac { 1 }{ 10^{ 10 } } \)

पाठ्य-पुस्तक पृष्ठ संख्या # 202

प्रयास कीजिए (क्रमांक 12.1)

प्रश्न 1.
गुणात्मक प्रतिलोम लिखिए –

1. 2^-4
2. 10^-5
3. 7^-2
4. 5^-3
5. 10^-100

हल:

1. 2^-4 का गुणात्मक प्रतिलोम = 2⁴
2. 10^-5 का गुणात्मक प्रतिलोम = 10⁵
3. 7^-2 का गुणात्मक प्रतिलोम = 7²
4. 5^-3 का गुणात्मक प्रतिलोम = 5³
5. 10^-100 का गुणात्मक प्रतिलोम = 10¹⁰⁰

प्रयास कीजिए (क्रमांक 12.2)

प्रश्न 1.
घातांकों का उपयोग करते हुए निम्न को विस्तारित रूप में लिखिए –

1. 1025.63
2. 1256.249

हल:
1. 1025.63 = 1 x 1000 + 2 x 10 + 5 x 1 + \(\frac{6}{10}\) + \(\frac{3}{100}\)
= 1 x 10³ + 2 x 10¹ + 5 x 10⁰ + 6 x 10^-1 + 3 x 10^-2

2. 1256.249 = 1 x 1000 + 2 x 100 + 5 x 10 + 6 x 1 + \(\frac{2}{10}\) + \(\frac{4}{100}\) + \(\frac{9}{1000}\)
= 1 x 10³ + 2 x 10² + 5 x 10¹ + 6 x 10⁰ + 2 x 10^-1 + 4 x 10^-2 + 9 x 10^-3

पाठ्य-पुस्तक पृष्ठ संख्या # 203

प्रयास कीजिए (क्रमांक 12.3)

प्रश्न 1.
घातांक रूप से सरल कीजिए और लिखिए –

1. (-2)^-3 x (-2)^-4
2. p³ x p^-10
3. 3² x 3^-5 x 3⁶

हल:
1. (-2)^-3 x (-2)^-4 = (-2) ^{(-3) + (-4)} = (-2)^-7
(∵ a^m x aⁿ = a^{m + 1})

2. p³ x p^-10 = p^3-10 = p^-7 = \(\frac { 1 }{ p^{ 7 } } \)

3. 3² x 3^-5 x 3⁶ = 3^2-5+6 = 3³

MP Board Class 8th Maths Solutions

MP Board Class 8th Maths Solutions Chapter 11 क्षेत्रमिति Ex 11.4

प्रश्न 1.
आपको एक बेलनाकार टैंक दिया हुआ है। निम्नलिखित में से किस स्थिति में आप उसका पृष्ठीय क्षेत्रफल ज्ञात करेंगे और किस स्थिति में आयत –

(a) यह ज्ञात करने के लिए कि इसमें कितना पानी रखा जा सकता है।
(b) इसका प्लास्टर करने के लिए वांछित सीमेंट बोरियों की संख्या।
(c) इसमें भरे पानी से भरे जाने वाले छोटे टैंकों की संख्या।

उत्तर:

(a) आयतन
(b) पृष्ठीय क्षेत्रफल
(c) आयतन।

प्रश्न 2.
बेलन A का व्यास 7 cm और ऊँचाई 14 cm है। बेलन B का व्यास 14 cm और ऊँचाई 7 cm है। परिकलन किए बिना क्या आप बता सकते हैं कि इन दोनों में किसका आयतन अधिक है? दोनों बेलनों का आयतन ज्ञात करते हुए इसका सत्यापन कीजिए। जाँच कीजिए कि क्या अधिक आयतन वाले बेलन का पृष्ठीय क्षेत्रफल भी अधिक है।

हल:
बेलन B का आयतन अधिक है।
बेलन A के लिए, r = \(\frac{7}{2}\) सेमी तथा h = 14 सेमी
बेलन A का आयतन = πr²h
= \(\frac{22}{7}\) x \(\frac{7}{2}\) x \(\frac{7}{2}\) x 14 सेमी³
= 539 सेमी³
बेलन B के लिए, r = \(\frac{14}{2}\) सेमी = 7 सेमी तथा h= 7 सेमी
बलेन B का आयतन = πr²h
= \(\frac{22}{7}\) x 7 x 7 x 7 सेमी³
= 1078 सेमी³
बेलन A का पृष्ठीय क्षेत्रफल = 2πr (r + h)
= 2 x \(\frac{22}{7}\) x \(\frac{7}{2}\) (\(\frac{7}{2}\) + 14) सेमी²
= 22 (\(\frac{7+28}{2}\)) सेमी²
= 11 x 35 सेमी² = 385 सेमी²
बेलन का पृष्ठीय क्षेत्रफल = 2πr (r + h)
= 2 x \(\frac{22}{7}\) x 7 (7 + 7) सेमी²
= 44 (14) सेमी²
= 616 सेमी
हाँ, अधिक आयतन वाले बेलन B का पृष्ठीय क्षेत्रफल भी अधिक है।

प्रश्न 3.
एक ऐसे घनाभ की ऊँचाई ज्ञात कीजिए जिसके आधार का क्षेत्रफल 180 cm² और जिसका आयतन 900 cm³ है।
हल:
यहाँ, घनाभ का आयतन = 900 सेमी³ तथा आधार का क्षेत्रफल = 180 सेमी²
माना कि घनाभ की ऊँचाई = h सेमी है।
घनाभ का आयतन = आधार का क्षेत्रफल x ऊँचाई
900 सेमी² = 180 सेमी² x h
h = \(\frac{900}{180}\) = 5 सेमी
अतः घनाभ की ऊँचाई = 5 सेमी

प्रश्न 4.
एक घनाभ की विमाएँ 60 cm x 54 cm x 30 cm हैं। इस घनाभ के अन्दर 6 cm भुजा वाले कितने छोटे घर रखे जा सकते हैं?
हल:
यहाँ, l = 60 सेमी
b = 54 सेमी तथा
h = 30 सेमी
घनाभ का आयतन = l x b x h
= 60 x 54 x 30 सेमी³
घन की भुजा = 6 सेमी
घन का आयतन = (भुजा)³ = (6)³ सेमी³
= 6 x 6 x 6 सेमी³
= 216 सेमी³

अतः घनाभ में 450 घन रखे जा सकते हैं।

प्रश्न 5.
एक ऐसे बेलन की ऊँचाई ज्ञात कीजिए जिसका आयतन 1.54 m³ और जिसके आधार का व्यास 140 cm है।
हल:
यहाँ, बेलन का आयतन = 1.54 मीटर
त्रिज्या r = \(\frac{140}{2}\) सेमी = 70 सेमी
= \(\frac{70}{100}\) मीटर = 0.7 मी
माना कि ऊँचाई = h है।
अब, बेलन का आयतन = πr²h
1.54 = \(\frac{22}{7}\) x 0.7 × 0.7 x h
h = \(\frac{1.54×7}{22×0.7×0.7}\) मीटर
= 1 मीटर
अतः बेलन की ऊँचाई = 1 मीटर

प्रश्न 6.
एक दूध का टैंक बेलन के आकार का है जिसकी त्रिज्या 1.5 m है और लम्बाई 7 m है। इस टैंक में भरे जा सकने वाले दूध की मात्रा लीटर में ज्ञात कीजिए।

हल:
टैंक की त्रिज्या = 1.5 m, टैंक की लम्बाई = 7 m
टैंक की धारिता = πr²h
= \(\frac{22}{7}\) x 1.5 x 1.5 x 7 मीटर³
= 49.5 मी³
= 49.5 x 1000 लीटर
(∵ 1 मी³ = 1000 लीटर)
= 49500 लीटर
अत: टैंक में भरे जाने वाली दूध की मात्रा = 49500 लीटर

प्रश्न 7.
किसी घन के प्रत्येक किनारे को दुगुना कर दिया जाए तो –

1. इसके पृष्ठीय क्षेत्रफल में कितने गुना वृद्धि होगी?
2. इसके आयतन में कितने गुना वृद्धि होगी?

हल:
माना कि घन की भुजा = x इकाई है, तब
इसका आयतन = x³ तथा पृष्ठीय क्षेत्रफल = 6x²
अब, जबकि घन के प्रत्येक किनारे को दुगुना कर दिया जाए, तब

1. इसका पृष्ठीय क्षेत्रफल = 6(2x)² = 6 x 4x²
= 24x² = 4 x 6x²
अतः नये घन के पृष्ठीय क्षेत्रफल में चार गुना वृद्धि होगी।

2. नये घन का आयतन = (2x)²
= 8x² = 8 × x³
अतः इसके आयतन में आठ गुना वृद्धि होगी।

प्रश्न 8.
एक कुंड के अन्दर 60 लीटर प्रति मिनट की दर से पानी गिर रहा है। यदि कुंड का आयतन 108 m’ है, _ तो ज्ञात कीजिए कि इस कुंड को भरने में कितने घंटे लगेंगे?

हल:
यहाँ, कुंड का आयतन
= 108 m³
= 108 x 1000 लीटर
= 108000 लीटर
कुंड में पानी गिरने की दर = 60 लीटर प्रति मिनट
= 60 x 60 लीटर प्रति घण्टा

= 30 घण्टे
अतः कुंड को भरने में 30 घण्टे लगेंगे।

MP Board Class 8th Maths Solutions

MP Board Class 8th Maths Solutions Chapter 11 क्षेत्रमिति Ex 11.3

प्रश्न 1.
दो घनाकार डिब्बे हैं जैसा कि संलग्न आकृति में दर्शाया गया है। किस डिब्बे को बनाने के लिए कम सामग्री की आवश्यकता है?

हल:
डिब्बे (a) के लिए –
l = 60 सेमी
b = 40 सेमी
h = 50 सेमी
डिब्बे (a) का कुल पृष्ठीय क्षेत्रफल = 2 (lb + bh + hl)
= 2 (60 x 40 + 40 x 50 + 50 x 60) वर्ग सेमी
= 2 (2400 + 2000 + 3000) वर्ग सेमी
= 2 (7400) वर्ग सेमी
=14800 वर्ग सेमी

डिब्बे (b) के लिए –
l = 50 सेमी
b = 50 सेमी
h = 50 सेमी
(∴ = b = h = 50 सेमी)
डिब्बे (b) का कुल पृष्ठीय क्षेत्रफल = 6l²
= 6 x (50)² वर्ग सेमी
=6 x 2500 वर्ग सेमी
= 15000 वर्ग सेमी
क्योंकि डिब्बे (a) का कुल पृष्ठीय क्षेत्रफल डिब्बे (b) के कुल पृष्ठीय क्षेत्रफल से कम है।
अतः (a) डिब्बे को बनाने के लिए कम सामग्री की आवश्यकता होगी।

प्रश्न 2.
80 cm x 48 cm x 24 cm माप वाले एक सूटकेस को तिरपाल के कपड़े से ढकना है। ऐसे 100 सूटकेसों को ढकने के लिए 96 cm चौड़ाई वाले कितने मीटर तिरपाल के कपड़े की आवश्यकता है?
हल:
सूटकेस का कुल पृष्ठीय क्षेत्रफल = 2 (80 x 48 + 48 x 24 + 24 x 80) सेमी²
= 2 (3840 + 1152 + 1920) सेमी²
= 2 x 6912 सेमी²
= 13824 सेमी²
100 सूटकेसों का पृष्ठीय क्षेत्रफल =100 x 13824 सेमी² = 100 x \(\frac{100×13824}{100×100}\) मीटर²
माना कि तिरपाल के कपड़े की आवश्यक लम्बाई = x मीटर तिरपाल के कपड़े का वांछित क्षेत्रफल = 100 सूटकेसों का क्षेत्रफल
x × \(\frac{96}{100}\) मी² = \(\frac{100×13824}{100×100}\) मी²
(∴ 96 cm = \(\frac{96}{100}\) m)
x = \(\frac{100x13824x100}{100x100x96}\) मी
= 144 मीटर
अतः 100 सूटकेसों को ढकने के लिए 144 मीटर तिरपाल के कपड़े की आवश्यकता होगी।

प्रश्न 3.
एक ऐसे घन की भुजा ज्ञात कीजिए जिसका पृष्ठीय क्षेत्रफल 600 cm² है।
हल:
माना कि घन की भुजा = l सेमी है।
घन का पृष्ठीय क्षेत्रफल = 6l²
अब, प्रश्नानुसार,
6l² = 600
l² = \(\frac{600}{6}\) = 100
या l = \(\sqrt{100}\) = 10 सेमी
अतः घन की भुजा = 10 सेमी

प्रश्न 4.
रुखसार ने 1 m x 2 m x 1.5 m माप वाली एक पेटी को बाहर से पेंट किया। यदि उसने पेटी के तल के अतिरिक्त उसे सभी जगह से पेंट किया हो तो ज्ञात कीजिए कि उसने कितने पृष्ठीय क्षेत्रफल को पेंट किया।

हल:
यहाँ, l = 2 मी
b = 1 मी तथा
h = 1.5 मी
पेंट किया हुआ क्षेत्रफल = lb + 2bh + 21h
= (2 x 1 + 2 x 1 x 1.5 + 2 x 2 x 1.5) मी²
= (2 + 3 + 6) मी²
= 11मी²
अतः रुखसार ने 11 मी² पृष्ठीय क्षेत्रफल को पेंट किया।

प्रश्न 5.
डैनियल एक ऐसे घनाभाकार कमरे की दीवारों और छत को पेंट कर रहा है जिसकी लम्बाई, चौड़ाई और ऊँचाई क्रमशः 15 m, 10 m एवं 7 m हैं। पेंट की प्रत्येक कैन की सहायता से 100 m² क्षेत्रफल को पेंट किया जा सकता है। तो उस कमरे के लिए उसे पेंट की कितनी कैनों की आवश्यकता होगी?
हल:
यहाँ, l = 15 मी
b = 10 मी
h = 7 मी
पेंट किया जाने वाला क्षेत्रफल = lb + 2bh + 2hl
= 15 x 10 + 2 x 10 x 7 + 2 x 7 x 15 मी²
= 150 + 140 + 210 मी²
= 500 मी²

अतः डैनियल को 5 पेंट की कैनों की आवश्यकता होगी।

प्रश्न 6.
वर्णन कीजिए कि दाईं तरफ दी गई आकृतियाँ किस प्रकार एकसमान हैं और किस प्रकार एक दूसरे से भिन्न-भिन्न हैं? किस डिब्बे का पार्श्व पृश्ठीय क्षेत्रफल अधिक है?

हल:
दोनों आकृतियाँ ऊँचाई में एकसमान हैं।
अन्तर:

1. एक आकृति बेलन है और दूसरी आकृति घन है।
2. बेलन के दो वृत्तीय फलक हैं, जबकि घन के छः वर्गाकार फलक हैं।

बेलन का पार्श्व पृष्ठीय क्षेत्रफल = 2πrh
यहाँ, l = 5 सेमी = 3.5 सेमी और
h = 7 सेमी
∴ बेलन का पार्श्व पृष्ठीय क्षेत्रफल = 2 x \(\frac{22}{7}\) x 3.5 x 7 वर्ग सेमी
= 154 वर्ग सेमी
घन की भुजा = 7 सेमी, ऊँचाई = 7 सेमी
घन का पार्श्व पृश्ठीय क्षेत्रफल = आधार की परिमाप x ऊँचाई
= 4 x 7 x 7 वर्ग सेमी
= 196 वर्ग सेमी
अत: घनाकार डिब्बे का पार्श्व पृष्ठीय क्षेत्रफल अधिक है।

प्रश्न 7.
7 m त्रिज्या और 3 m ऊँचाई वाला एक बन्द बेलनाकार टैंक किसी धातु की एक चादर से बना हुआ है। उसे बनाने के लिए वांछित धातु की चादर की मात्रा ज्ञात कीजिए।
हल:
यहाँ, बेलनाकार टैंक की त्रिज्या r = 7 मी और
ऊँचाई h = 3 मी
बन्द बेलनाकार टैंक बनाने के लिए वांछित चादर = बेलन का कुल पृष्ठीय क्षेत्रफल
= 2πr (r + h)
= 2 x \(\frac{22}{7}\) x 7x (7 + 3) मी²
= 44 x 10 मी²
= 440 मी²
अत: टैंक बनाने के लिए वांछित धातु की चादर का क्षेत्रफल = 440 मी²

प्रश्न 8.
एक खोखले बेलन का वक्र पृष्ठीय क्षेत्रफल 4224 cm² है। इसे इसकी ऊँचाई के अनुदिश काटकर 32 cm चौड़ाई की एक आयताकार चादर बनाई जाती है। आयताकार चादर का परिमाप ज्ञात कीजिए।
हल:
यहाँ, बेलन का वक्र पृष्ठीय क्षेत्रफल = 4224 cm²
आयताकार चादर की चौड़ाई = 32 cm
खोखले बेलन को काटकर आयताकार चादर बनाई गई है।
∴ बेलन के आधार की परिमाप = आयताकार चादर की लम्बाई तथा बेलन की ऊँचाई = चादर की चौड़ाई
इसलिए, बेलन का वक्र पृष्ठीय क्षेत्रफल = आयताकार चादर का क्षेत्रफल माना कि चादर की लम्बाई = l सेमी है।
∴ आयताकार चादर का क्षेत्रफल = बेलन का वक्र पृष्ठीय क्षेत्रफल
l x 32 = x 4224
l = \(\frac{4224}{32}\) सेमी = 132 सेमी
अब, आयताकार चादर की परिमाप = 2 (l + b)
= 2 (132 + 32) सेमी
= 2 x 164 सेमी
= 328 सेमी
अत: आयताकार चादर का अभीष्ट परिमाप = 328 सेमी

प्रश्न 9.
किसी सड़क को समतल करने के लिए एक सड़क रोलर को सड़क के ऊपर एक बार घूमने के लिए 750 चक्कर लगाने पड़ते हैं। यदि सड़क रोलर का व्यास 84 cm और लम्बाई 1 m है तो सड़क का क्षेत्रफल ज्ञात कीजिए।

हल:
रोलर बेलनाकार है।
रोलर की त्रिज्या r = \(\frac{84}{2}\) सेमी = 42 सेमी = 0.42 मीटर
रोलर की लम्बाई h = 1 मीटर
बेलन का वक्र पृष्ठीय क्षेत्रफल = 2πrh
= 2 x \(\frac{22}{7}\) = x 0.42 x 1 मी²
= 2.64 मी²
रोलर द्वारा 750 चक्कर में तय किया क्षेत्रफल = 750 x 2.64 मी² = 1980 मी²
अत: सड़क का क्षेत्रफल = 1980 मी²

प्रश्न 10.
एक कम्पनी अपने दूध पाउडर को ऐसे बेलनाकार बर्तनों में पैक करती है जिनका व्यास 14 cm और ऊँचाई 20 cm है। कम्पनी बर्तन के पृष्ठ के चारों ओर एक लेबल लगाती है (जैसा कि आकृति में दर्शाया गया है)। यदि यह लेबल बर्तन के तल और शीर्ष दोनों से 2 cm की दूरी पर चिपकाया जाता है तो लेबल का क्षेत्रफल क्या है?

हल:
यहाँ, बेलनाकार बर्तन का व्यास = 14 सेमी
∴ बेलनाकार बर्तन की त्रिज्या l = 14 सेमी = 7 सेमी
बेलनाकार बर्तन की ऊँचाई = 20 सेमी
∴ कम्पनी ने बर्तन में लेबल बर्तन के तल और शीर्ष दोनों से 2 सेमी की दूरी पर चिपकाया है। बर्तन पर चिपका हुआ लेबल एक बेलन निर्मित करता है, जिसकी त्रिज्या l = 7 सेमी तथा ऊँचाई = 20 – 4 = 16 सेमी
∴ लेबल का वक्र पृष्ठीय क्षेत्रफल= 2πrh = 2 x \(\frac{22}{7}\) x 7 x 16 सेमी²
= 704 सेमी²
अतः लेबल का क्षेत्रफल = 704 सेमी²

पाठ्य-पुस्तक पृष्ठ संख्या # 196

घनाभ

प्रश्न 1.
(i) निम्नलिखित सारणी पर विचार कीजिए और रिक्त स्थानों की पूर्ति कीजिए –
उत्तर:

प्रश्न 1.
(ii) आप क्या देखते करते हैं?
उत्तर:
हम यहाँ यह देखते हैं कि घनाभों को बनाने के लिए 36 घनों का उपयोग किया गया है। इसलिए प्रत्येक घनाभ का आयतन 36 घन इकाई है।
स्पष्ट है कि घनाभ का आयतन = लम्बाई x चौड़ाई x ऊँचाई
अर्थात् घनाभ का आयतन = आधार का क्षेत्रफल x ऊँचाई

पाठ्य-पुस्तक पृष्ठ संख्या # 197

प्रयास कीजिए (क्रमांक 11.10)

प्रश्न 1.
निम्नलिखित घनाभों (आकृति 11.45) का आयतन ज्ञात कीजिए –

हल:
1. यहाँ, 1 = 8 सेमी, b = 3 सेमी तथा h = 2 सेमी
घनाभ का आयतन = l x b x h
= 8 x 3 x 2 = 48 सेमी³

2. यहाँ, आधार का क्षेत्रफल = l x b = 24 सेमी²
ऊँचाई h = 3 सेमी = 100 मी
घनाभ का आयतन = आधार का क्षेत्रफल x ऊँचाई
= 24 मी² x \(\frac{3}{100}\)मी = \(\frac{72}{100}\)मी³
= 0.72 मी³

घनाभ

प्रयास कीजिए (क्रमांक 11.11)

प्रश्न 1.
निम्नलिखित घनों का आयतन ज्ञात कीजिए –

1. 4 cm भुजा वाला
2. 1.5 m भुजा वाला।

हल:
1. यहाँ, घन की भुजा l = 4 सेमी
∴ घन का आयतन = l³ = (4)³सेमी
= 4 x 4 x 4 सेमी
= 64 सेमी³

2. यहाँ, घन की भुजा l = 1.5 मी
∴ घन का आयतन = = (1.5)³मी
= 1.5 x 1.5 x 1.5 मी³ = 3.375 मी³

इन्हें कीजिए (क्रमांक 11.5)

प्रश्न 1.
समान आकार वाले 64 घनों को जितने रूपों में आप व्यवस्थित कर सकते हैं, उतने रूपों में व्यवस्थित करते हुए घनाभ बनाइए। प्रत्येक रूप का पृष्ठीय क्षेत्रफल ज्ञात कीजिए। क्या समान आयतन वाली ठोस आकृतियों का पृष्ठीय क्षेत्रफल समान होता है?
हल:
कुछ व्यवस्थित रूप इस प्रकार हो सकते हैं। घन इस प्रकार रख सकते हैं –

इनके पृष्ठीय क्षेत्रफल क्रमशः इस प्रकार हैं –
∴ पृष्ठीय क्षेत्रफल = 2 (lb + bh + hl)

(i) ∴ पृष्ठीय क्षेत्रफल = 2 (64 x 1 + 1 x 1 + 1 x 64)
= 2 x (64 + 1 + 64)
= 2 x 129
= 258 वर्ग इकाई

(ii) पृष्ठीय क्षेत्रफल = 2 (32 x 2 + 2 x 1 + 1 x 32)
= 2 (64 + 2 + 32)
= 2 x 98
= 196 वर्ग इकाई

(iii) पृष्ठीय क्षेत्रफल = 2 (16 x 2 + 2 x 2 + 2 x 16)
= 2(32 + 4 + 32)
= 2 x 68
= 136 वर्ग इकाई

(iv) पृष्ठीय क्षेत्रफल = 2 (16 x 4 +4 x 1 + 1 x 16)
= 2 (64 + 16 + 16)
= 2 x 84
= 168 वर्ग इकाई

(v) पृष्ठीय क्षेत्रफल = 2 (8 x 4 + 4 x 2 + 2 x 8)
= 2 (32 + 8 + 16)
= 2 x 56
= 112 वर्ग इकाई

(vi) पृष्ठीय क्षेत्रफल = 2 (4 x 4 + 4 x 4 + 4 x 4)
= 2 (16 + 16 + 16)
= 2 x 48
= 96 वर्ग इकाई
प्रत्येक स्थिति में आयतन = 64 घन इकाई
यहाँ, स्पष्ट है कि प्रत्येक घन का आयतन तो समान है परन्तु पृष्ठीय क्षेत्रफल भिन्न हैं।
अतः समान आयतन वाली ठोस आकृतियों का पृष्ठीय क्षेत्रफल समान नहीं होता है।

सोचिए, चर्चा कीजिए और लिखिए (क्रमांक 11.6)

प्रश्न 1.
एक कम्पनी बिस्कुट बेचती है। बिस्कुटों को पैक करने के लिए घनाभाकार डिब्बों का उपयोग किया जा रहा है। डिब्बा A → 3 cm x 8 cm x 20 cm, डिब्बा B → 4 cm x 12 cm x 10 cm. डिब्बे का कौन सा आकार कम्पनी के लिए आर्थिक दृष्टि से लाभदायक रहेगा? क्यों? क्या आप ऐसे किसी और आकार (विमाएँ) के डिब्बे का सुझाव दे सकते हैं जिसका आयतन इनके समान हो परन्तु इनकी तुलना में आर्थिक दृष्टि से अधिक लाभदायक हो?
हल:
डिब्बा A:
l = 3 सेमी
b = 8 सेमी
h = 20 सेमी
आयतन = l x b x h = 3 x 8 x 20 सेमी³ = 480 सेमी³
पृष्ठीय क्षेत्रफल = 2 (lb + bh + hl)
= 2 (3 x 8 + 8 x 20 + 20 x 3) सेमी²
= 2 (24 + 160 + 60) सेमी²
= 2 x 244 सेमी²
= 488 सेमी²

डिब्बा B:
l = 4 सेमी
b = 12 सेमी
h = 10 सेमी
आयतन = l x b x h = 4 x 12 x 10 सेमी³ = 480 सेमी³
पृष्ठीय क्षेत्रफल = 2 (lb + bh + hl)
= 2(4 x 12 + 12 x 10 + 10 x 4) सेमी²
= 2 (48 + 120 + 40) सेमी²
= 2 x 208 सेमी²
= 416 सेमी²
यहाँ, डिब्बे A का आयतन = डिब्बे B का आयतन है।
परन्तु डिब्बे A का पृष्ठीय क्षेत्रफल डिब्बे B के पृष्ठीय क्षेत्रफल से अधिक है।
अतः डिब्बा B को बनाने में कम सामग्री की आवश्यकता होगी।
∴ डिब्बे A की अपेक्षा डिब्बा B का आकार कम्पनी के के लिए आर्थिक दृष्टि से अधिक लाभदायक रहेगा।

अन्य डिब्बा:
8 सेमी x 6 सेमी x 10 सेमी
इस डिब्बे का आयतन = 8 x 6 x 10 = 480 सेमी³
इसका पृष्ठीय क्षेत्रफल = 2 (8 x 6+ 6 x 10 + 10 x 8) सेमी²
= 2(48 + 60 + 80) सेमी²
= 2 x 188 सेमी²
= 376 सेमी²
स्पष्ट है कि इस डिब्बे का आयतन डिब्बे B के आयतन के बराबर है। परन्तु इसका पृष्ठीय क्षेत्रफल डिब्बे B के पृष्ठीय क्षेत्रफल से कम है।
अतः दिए हुए डिब्बों की अपेक्षा यह डिब्बा आर्थिक दृष्टि से अधिक लाभदायक है।

पाठ्य-पुस्तक पृष्ठ संख्या # 198

आयतन और धारिता

प्रयास कीजिए (क्रमांक 11.12)

प्रश्न 1.
संलग्न बेलनों का आयतन ज्ञात कीजिए –

हल:
(i) यहाँ, बेलन की त्रिज्या r = 7 सेमी
ऊँचाई h = 10 सेमी
बेलन का आयतन = πr²h
= \(\frac{22}{7}\) x 7 x 7 x 10 सेमी³
= 1540 सेमी³

(ii) यहाँ आधार का क्षेत्रफल πr² = 250 मी तथा ऊँचाई = 2 मी
बेलन का आयतन = आधार का क्षेत्रफल x ऊँचाई
= 250 मी² x 2 मी
= 500 मी³

MP Board Class 8th Maths Solutions

MP Board Class 8th Sanskrit Model Question Paper (आदर्श प्रश्नपत्रम्)

प्रश्न 1.
(अ) समुचित चित्वां लिखत (उचित शब्द चुनकर लिखिए)
(क) कार्यक्षेत्रे (कार्य के क्षेत्र में-)
(अ) तरणीयम्
(ब) त्वरणीयम्
(स) वदनीयम्
(द) स्मरणीयम्।
उत्तर:
(ब) त्वरणीयम्। (शीघ्रता करनी चाहिए।)

(ख) गुरुत्वाकर्षणस्य सिद्धान्तः प्रतिपादितः (गुरुत्वाकर्षण के सिद्धान्त का प्रतिपादन किया-)
(अ) आदित्यदासेन
(ब) आर्यभट्टेन
(स) वराहमिहिरेण
(द) मोहनदासेन
उत्तर:
(स) वराहमिहिरेण। (वराहमिहिरेण)

(ग) वसन्तपञ्चमी पर्व भवति (वसन्त पंचमी का पर्व होता है-)
(अ) फाल्गुनमासे
(ब) माघमासे
(स) चैत्रमासे
(द) कार्तिकमासे।
उत्तर:
(ब) माघमासे। (माघ के महीने में।)

(घ) अहिल्याबाई इत्यस्याः पत्युः नाम आसीत् (अहिल्याबाई इनके पति का नाम था-)
(अ) दामोदररावः
(ब) खण्डेराव:
(स) कृष्णरावः
(द) श्यामरावः
उत्तर:
(ब) खण्डेरावः। (खण्डेराव।)

(ङ) सर्वः पश्यतु (सब देखें-)
(अ) दूरदर्शनम्
(ब) कार्याणि
(स) अभद्राणि
(द) भद्राणि।
उत्तर:
(द) भद्राणि। (सुखों को।)

(ब) प्रदत्तैः शब्दैः रिक्तस्थानानि पूरयत (दिये गये शब्दों से रिक्त स्थानों की पूर्ति करो-)
(प्रकृतिहिताय, रामकृष्णपरमहंसः, मेकलसुता, शीलं, एकादशवर्षाणि)
(क) नर्मदायाः अपरं नाम ………… अस्ति।
(ख) ………… सर्वत्र वै धनम्।
(ग) प्रवर्ततां ……….. पार्थिवः।
(घ) चित्रकूटे रामचन्द्रः ………… यावत् निवासं कृतवान्।
(ङ) स्वामिविवेकानन्दस्य गुरुः ……….. आसीत्।
उत्तर:
(क) मेकलसुता
(ख) शीलं
(ग) प्रकृतिहिताय
(घ) एकादशवर्षाणि
(ङ) रामकृष्णपरमहंसः।

प्रश्न 2.
अधोलिखितगद्यांशं पठित्वा प्रश्नानाम् उत्तराणि संस्कृते लिखत (नीचे लिखे गद्यांश को पढ़कर प्रश्नों के उत्तर संस्कृत में लिखो-)

कस्मिश्चित् वने निम्बवृक्षे एकं चटकायुगलं प्रतिवसति स्म। समये चटकया अण्डानि दत्तानि, युगलम् अति प्रसन्नम् आसीत्। एकस्मिन् दिने आतपपीडितः एकः मदमत्तः गजः तत्र आगतः। मदेन सः तस्य वृक्षस्य तां शाखां नाशितवान् यस्यां शाखायां चटकायाः अण्डानि आसन्। अतः अण्डानि अपि नष्टानि।

(क) चटकायुगलं कस्मिन् वृक्षे प्रतिवसति स्म? (चिड़ियों का जोड़ा किस वृक्ष के नीचे रहता। था?)
उत्तर:
चटकायुगलं निम्बवृक्षे प्रतिवसति स्म। (चिड़ियों का जोड़ा नीम के वृक्ष के नीचे रहता था।)

(ख) अण्डानि कया दत्तानि? (अण्डे किसके द्वारा दिये गये?)
उत्तर:
अण्डानि चटकया दत्तानि। (अण्डे चिड़िया द्वारा दिये गये।)

(ग) एकस्मिन् दिने कः तत्र आगतः? (एक दिन कौन वहाँ आया?)
उत्तर:
एकस्मिन् दिने एकः मदमत्तः गजः तत्र आगतः। (एक दिन एक मतवाला हाथी वहाँ आया।)

(घ) मदेन गजः कां नाशितवान्? (मस्ती में हाथी ने क्या-क्या तोड़ दिया?)
उत्तर:
मदेन गजः वृक्षस्य तां शाखां नाशितवान् यस्यां शाखायां चटकायाः अण्डानि आसन्। (मस्ती में हाथी ने वृक्ष की उस डाल को तोड़ दिया जिस पर चिड़िया के अण्डे थे।)
अथवा

एकदा विक्रमादित्यः नगरभ्रमणसमये एक मरणासन्नं रूग्णं दृष्टवान। तस्य दर्शनेन मनसि वैराग्यम् उद्भूतम्। अतः मायामोहमयं संसारं ज्ञात्वा सः महामन्त्रिणि राज्यभारं समर्प्य :वनम् अगच्छत्।

(क) विक्रमादित्यः नगरभ्रमणसमे कं दृष्टवान्? (विक्रमादित्यः ने नगर में भ्रमण के समय किसको देखा?)
उत्तर:
विक्रमादित्य नगरभ्रमणसमये एकं मरणासन्नं रुग्णं दृष्टवान। (विक्रमादित्य ने नगर भ्रमण के समय एक मरणासन्न रोगी को देखा।)

(ख) विक्रमादित्यस्य मनसि किम् उद्भूतम्? (विक्रमादित्य के मन में क्या उत्पन्न हुआ?)
उत्तर:
विक्रमादित्य मनसि वैराग्यम् उद्भूतम्। (विक्रमादित्य के मन में वैराग उत्पन्न हुआ।)

(ग) सः महामन्त्रिणि किं समर्प्य वनम् अगच्छत्? (वह महामन्त्री को क्या सौंपकर वन चले गये?)
उत्तर:
सः महामन्त्रिणि राज्यभारं समर्प्य वनम् अगच्छत्। (वह महामन्त्री को राज्यभार सौंपकर वन चले गये।)

(घ) ‘अगच्छत्’ इत्यस्मिन् पदे कः धातुः? (‘अगच्छत्’ शब्द में कौन-सी धातु है?)
उत्तर:
‘अगच्छत्’ इत्यस्मिन् पदे ‘गमः’ धातुः। (‘अगच्छत्’ शब्द में ‘गम्’ (जाना) धातु हैं।)

प्रश्न 3.
अधोलिखितपद्यांश पठित्वा प्रश्नानाम् उत्तराणि संस्कृत लिखत (नीचे लिखे पद्यांश को पढ़कर प्रश्नों के उत्तर संस्कृत में लिखो)
उद्योगे नास्ति दारिद्रयं जपतो नास्ति पातकम्।
मौने च कलहो नास्ति नास्ति जागरिते भयम्।।

(क) उद्योगे किं नास्ति? (परिश्रम करने से क्या नहीं रहता है?)
उत्तर:
उद्योगे दारिद्रयं नास्ति। (परिश्रम करने से गरीबी नहीं रहती है।)

(ख) जपतो किं नास्ते? (भगवान का स्मरण करने से क्या नहीं रहता है?)
उत्तर:
जपतो पातकं नास्ति। (भगवान का स्मरण करने से पाप नहीं रहता है।)

(ग) भयं कदा नास्ति? (भय कब नहीं रहता है?)
उत्तर:
जागरिते भयं नास्ति। (जागने पर भय नहीं रहता है।)

(घ) ‘मौने’ इत्यस्मिन् पदे का विभक्तिः किं च वचनम्? (‘मौने’ शब्द में कौन-सी विभक्ति और कौन-सा वचन है?)
उत्तर:
‘मौने’ इत्यस्मिन् पदे सप्तमी विभक्ति एकं च वचनम्। (‘मौने’ शब्द में सप्तमी विभक्ति और एकवचन है।)
अथवा

माता गुरुतरा भूमैः खात्पितोच्चतरस्तथा।
मनः शीघ्रतरं वाताच्चिन्ता बहुतरी तृणात्॥

(क) भूमेः गुरुतरा का? (पृथ्वी से भारी कौन है?)
उत्तर:
भूमेः गुरुतरा माता। (पृथ्वी से भारी माता है।)

(ख) खात् उच्चतरः कः? (आकाश से ऊँचा कौन है?)
उत्तर:
खात् उच्चतरः पिता। (आकाश से ऊँचा पिता है।)

(ग) वातात् शीघ्रतरं किम्? (वायु से तेज चलने वाली कौन है?)
उत्तर:
वातात् शीघ्रतरं मनः। (वायु से तेज चलने वाला मन है।)

(घ) ‘तृणात्’ इत्यस्मिन् पदे विभक्ति वचनं च लिखत? (‘तृणात्’ शब्द में विभक्ति और वचन को लिखिए।)
उत्तर:
‘तृणात्’ इत्यस्मिन् पदे पञ्चमी विभक्ति एकं वचनं च अस्ति। (‘तृणात्’ शब्द में पंचमी विभक्ति एकवचन है।)

प्रश्न 4.
(अ) पाठ्यपुस्तकात् कण्ठस्थीकृतम् एक सुभाषितश्लोकं लिखत यः अस्मिन् प्रश्नपत्रे नास्ति। (पाठ्यपुस्तक से कण्ठस्थ किया हुआ एक सुभाषित श्लोक लिखो जो इस प्रश्न-पत्र में नहीं आया है।)
उत्तर:
अयं निजः परोयेति गणना लप्पुचेतसाम्। उर्दचरितानां तु वसुधैव कुटुम्बकम्।।

(ब) श्लोकपूर्तिं कुरुत (श्लोक पूर्ति करो-)
विना वेदं विना ………….. विना ………… कथाम्।
विना …………. भारतं न हि।।
उत्तर:
विना वेदं विना गीतां, विना रामायणी कथाम्।
विना कविं कालिदास, भारतं भारतं न हि।।

(स) पाठ्यपुस्तकात् कण्ठस्थीकृताम् एकां सूक्ति लिखत। (पाठ्यपुस्तक से कण्ठस्थ की हुई एक सूक्ति लिखो।)
उत्तर:
विद्वान् सर्वत्र पूज्यते।’

प्रश्न 5.
(अ) अधोलिखितेषु (5) पञ्चप्रश्नानाम् उत्तराणि एकपदेन संस्कृत लिखत (निम्नलिखित में से पाँच प्रश्नों के उत्तर एक शब्द में संस्कृत में लिखो-)
(क) कस्मिन् मासे गणतन्त्रदिवसः भवति? (किस महीने में गणतन्त्र दिवस होता है?)
उत्तर:
‘जनवरिमासे’। (जनवरी महीने में।)

(ख) विद्या कीदृशी भवेत? (विद्या कैसी होनी चाहिए?)
उत्तर:
अर्थकरी। (धन का संग्रह करने वाली।)

(ग) विषपानं कः कृतवान्? (विषपानं किसने किया?)
उत्तर:
वीरः हरदौलः। (वीर हरदौल ने।)

(घ) चन्द्रशेखरस्ये पितुः नाम किम्? (चन्द्रशेखर के पिता का नाम क्या था?)
उत्तर :
सीतारामतिवारी। (सीताराम तिवारी।)

(ङ) नर्मदा कस्मात् स्थानात् प्रादुर्भवति? (नर्मदा किस स्थान से निकलती है?)
उत्तर:
अमरकण्टकपर्वतात्। (अमरकण्टक पर्वत से।)

(च) अहिल्यायाः जन्मग्रामः कः? (अहिल्या का जन्म किस गाँव में हुआ?)
उत्तर:
चौण्डी। (चौण्डी)

(छ) मेघदूतस्य कविः कः? (मेघदूत के कवि कौन हैं?)
उत्तर:
कालिदासः। (कालिदास।)

(ब) अधोलिखितेषु (5) पञ्चप्रश्नानाम् उत्तराणि एकवाक्येन संस्कृते लिखत (निम्नलिखित में पाँच प्रश्नों के उत्तर एक वाक्य में संस्कृत में लिखो-)
(क) कुत्र चरणीयम्? (कहाँ चढ़ना चाहिए?)
उत्तर:
कष्टपर्वते चरणीयम्। (कष्टरूपी पर्वत पर चढ़ना चाहिए।)

(ख) गुणेषु कः करणीयः? (गुणों के उपार्जन हेतु क्या करना चाहिए?)
उत्तर:
गुणेषु यत्नः करणीयः। (गुणों के उपार्जन हेतु प्रयास करने चाहिए।)

(ग) यूनां प्रेरकः पथप्रदर्शकश्च कः? (युवाओं के प्रेरक और पथ प्रदर्शक कौन हैं?)
उत्तर:
यूनां प्रेरकः पथ-प्रदर्शकश्च स्वामी विवेकानन्द:। (युवाओं के प्रेरक और पथ प्रदर्शक स्वामी विवेकानन्द हैं।)

(घ) चित्रकूटे कः विश्वविद्यालयः अस्ति? (चित्रकूट में कौन-सा विश्वविद्यालय है?)
उत्तर:
चित्रकूटे महात्मागान्धि ग्रामोदय विश्वविद्यालयः अस्ति। (चित्रकूट में महात्मा गाँधी ग्रामोदय विश्वविद्यालय है।)

(ङ) विक्रमादित्यस्य ध्येयवाक्यं किम् आसीत्? (विक्रमादित्य का ध्येय वाक्य क्या था?)
उत्तर:
विक्रमादित्यस्य ध्येयवाक्यं ‘सत्कर्म एव धर्म’ इति आसीत्। (विक्रमादित्य का ध्येय वाक्य ‘सत्कर्म ही धर्म है’ था।)

(च) काशीतलवाहिनी का? (काशी सतह में बहने वाली कौन नदी है?)
उत्तर:
काशीतलवाहिनी गङ्गा। (काशी सतह में बहने वाली गंगा है।)

(छ) पञ्चशाकानां नामानि लिखत। (पाँच सब्जियों के नाम लिखो।)
उत्तर:
पञ्चशाकानां नामानि आलुकं, पलाण्डुः, कुण्माण्ड, शिम्बां, मूलिका च इति सन्ति। (पाँच सब्जियों के नाम आलू, प्याज, कद्दू, सेम और मूली हैं।)

प्रश्न 6.
(अ) अधोलिखितेषु (2) द्वयोः शब्दरूपाणि निर्देशानुसार त्रिषु वचनेषु लिखत। (निम्नलिखित में से दो के शब्द रूप निर्देशानुसार तीनों वचनों में लिखो-)
(क) बालक-प्रथमा
(खा) मातृ -द्वितीया
(ग) राजन्-षष्ठी।
उत्तर:
(क) बालकः बालकौ बालकाः।
(ख) मातरम् मातरौ मातृः।
(ग) राज्ञः राज्ञोः राज्ञाम्।

(ब) अधोलिखितेषु (2) द्वयोः धातुरूपाणि निर्देशानुसारं त्रिषु वचनेषु लिखत (निम्नलिखित में से दो के धातु रूप निर्देशानुसार तीनों वचनों में लिखो-)
(क) वद्-लट्लकारः (वर्तमानकाल:) प्रथमपुरुषः।
उत्तर:
वदति वदतः वदन्ति।

(ख) सेव्-लुट्लकारः (भविष्यकाल:) मध्यमपुरुषः।
उत्तर:
सेविष्यसेसेविष्येथेसेविष्यध्वे।

(ग) लिख्-लङ्लकारः (भूतकालः) उत्तमपुरुषः।
उत्तर:
अलिखम् अलिखाव अलिखाम।

(स) अधोलिखितेषु (4) चत्वारि अशुद्धवाक्यानि शुद्धं कुरुत (निम्नलिखित में से चार अशुद्ध वाक्यों को शुद्ध करो)
(क) श्रीगणेशं नमः।
(ख) सः पुस्तक पठसि।
(ग) कृष्णः यानात् गच्छति।
(घ) छात्रः फलं खादामि।
(ङ) लक्ष्मणः रामस्य सह क्रीडति।
(च) गीता बालकं भोजनं ददाति
उत्तर:
(क) श्री गणेशाय नमः।
(ख) सः पुस्तकं पठति।
(ग) कृष्णः यानेन गच्छति।
(घ) छात्रः फलं खादति।
(ङ) लक्ष्मणः रामेण सह क्रीडति।
(च) गीता बालकाय भोजनं ददाति।

प्रश्न 7.
(अ) अधोलिखितेषु (3) त्रयाणां धातुं प्रत्ययं च पृथक् कुरुत (निम्नलिखित में से तीन के धातु और प्रत्यय अलग-अलग करो-)
(क) पठितुम्
(ख) गत्वा
(ग) गतः
(घ) खादितवान।
उत्तर:
(क) पठ् धातुः, तुमुन प्रत्ययः।
(ख) गम् धातुः, क्त्वा प्रत्ययः।
(ग) गम् धातुः, क्त प्रत्ययः।
(घ) खाद् धातुः, क्तवतु प्रत्ययः।

(ब) अधोलिखितेषु (2) द्वौ उपसर्गौ योजयित्वा पदनिर्माणं कुरुत (निम्नलिखित में से दो उपसर्ग जोड़कर शब्द बनाओ-)
(क) प्र
(ख) अनु
(ग) सु।
उत्तर:
(क) प्रहारः
(ख) अनुभवः
(ग) सुविचारः।

(स) अधोलिखितेषु (2) द्वयो अव्ययोः प्रयोगं कृत्वा वाक्यनिर्माणं कुरुत (निम्नलिखित में से दो अव्ययों का प्रयोग करके वाक्य। बनाओ-)
(क) अद्य
(ख) न
(ग) प्रायः।
उत्तर:
(क) अद्य वयं विद्यालयं गच्छामः।
(ख) अहम् श्वः मन्दिरं न गमिष्यामि।
(ग) प्रायः सर्वेः जनाः धनमिच्छन्ति।

प्रश्न 8.
(अ) अधोलिखितेषु (3) त्रयाणां पदानां सन्धिविच्छेदं कृत्वा सन्धिनाप लिखत (निम्नलिखित में से तीन पदों का सन्धि विच्छेद करके सन्धि का नाम लिखो-)
(क) विद्यालयः
(ख) सज्जनः
(ग) नमस्ते
(घ) महोत्सवः।
उत्तर:
(क) विद्या + आलयः (स्वर सन्धिः)
(ख) सत् + जनः (व्यञ्जन सन्धिः),
(ग) नमः + ते (विसर्ग सन्धिः),
(घ) महा + उत्सवः (स्वर सन्धि।)

(ब) अधोलिखितेषु (3) त्रयाणां पदानां समासविग्रहं कृत्वा समासनाम लिखत (निम्नलिखित में तीन पदों का समास विग्रह करके समास का नाम लिखो-)
(क) राजपुत्रः
(ख) महापुरुषः
(ग) पितरौ
(घ) चन्द्रशेखरः
उत्तर:
(क) राज्ञः पुत्रः (षष्ठी तत्पुरुषः समासः)
(ख) महान् चासौ पुरुषः (कर्मधारय समासः)
(ग) माता च पिता च (द्वन्द्व समासः)
(घ) चन्द्रःशेखरे यस्य सः (शिवः) (बहुव्रीहि समासः)

(स) अधोलिखतेषु (3) तिस्रः सङख्याः संस्कृते लिखत् (निम्नलिखित में से तीन संख्याओं को संस्कृत में लिखो-)
(क) 28
(ख) 36
(ग) 41
(घ) 46
उत्तर:
(क) अष्टाविंशतिः
(ख) षट्त्रिंशत्
(ग) एकचत्वारिंशत्
(घ) षट्चत्वारिंशत्।

प्रश्न 9.
अधोलिखितपदैः पत्रं पूरयत(निम्नलिखित शब्दों में से पत्र को पूरा करो-) (पीडितः, अवकाशं, निवेदनम्, अद्य, आगन्तुं)
सेवायाम्
श्रीमान् प्रधानाध्यापकमहोदयः
शासकीयमाध्यमिकविद्यालयाः
जाबलिपुरम्
महोदय!
विनम्र ………. अस्ति यत् अहम् ………. शीतज्वरेण ………. अस्मि। अतएव विद्यालयम् ………. न शक्नोमि। अतः एकदिवसीयम् ………. स्वीकरोतु।

भवतः आज्ञाकारी शिष्याः
दिनाङ्क : 22 फरवरीमास: 2009 ई.
अजयः
अष्टमकक्षा

उत्तर:
निवेदनम्, अद्य, पीडितः, आगन्तुं, अवकाशं।

MP Board Class 8th Sanskrit Solutions