Category: Class 6

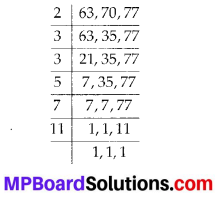
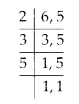
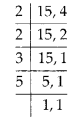
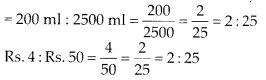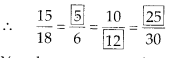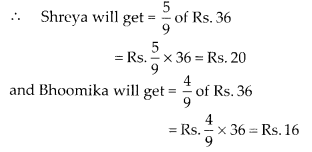MP Board Class 6th Maths Solutions Chapter 4 Basic Geometrical Ideas Ex 4.2

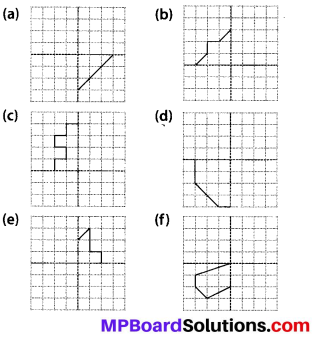
Question 1.
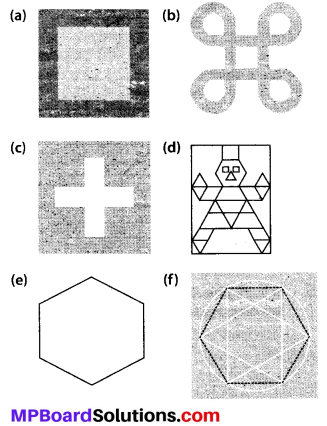
Classify the following curves as
(i) Open or
(ii) Closed.

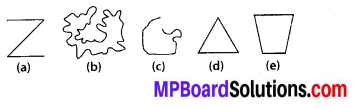
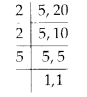
Solution:
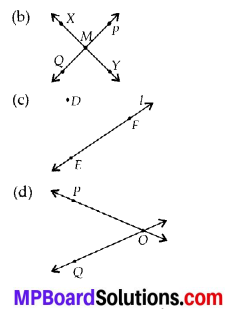
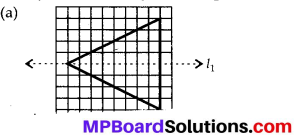
(a) Open curve
(b) Closed curve
(c) Open curve
(d) Closed curve
(e) Closed curve

Question 2.
Draw rough diagrams to illustrate the following:
(a) Open curve
(b) Closed curve.
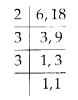
Solution:
(a) Open curves :

(b) Closed curves :

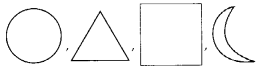
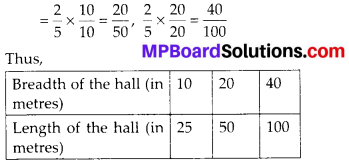
Question 3.
Draw any polygon and shade its interior.
Solution:

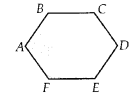
ABCDEF is the required polygon.

Question 4.
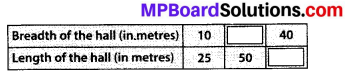
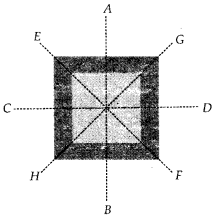
Consider the given figure and answer the questions:
(a) Is it a curve?
(b) Is it closed?
Solution:

(a) Yes, it is a curve.
(b) Yes, it is closed.

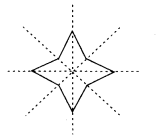
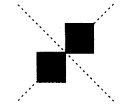
Question 5.
Illustrate, if possible, each one of the following with a rough diagram:
(a) A closed curve that is not a polygon.
(b) An open curve made up entirely of line segments.
(c) A polygon with two sides.
Solution:

(c) Polygon with two sides cannot be drawn.

MP Board Class 6th Maths Solutions

MP Board Class 6th Maths Solutions Chapter 4 Basic Geometrical Ideas Ex 4.1

Question 1.
Use the figure to name :

(a) Five points
(b) A line
(c) Four rays
(d) Five line segments
Solution:
(a) Five points : O, B, C, D, E
(b) A line \(\overleftrightarrow { DB }\)
(c) Four rays \(\overrightarrow{O D}\), \(\overrightarrow{O E}\), \(\overrightarrow{O C}\), \(\overrightarrow{O B}\)
(d) Five line segments :
\(\overline{D E}\), \(\overline{O E}\), \(\overline{O C }\), \(\overline{O B}\), \(\overline{O D}\).

Question 2.
Name the line given in all possible (twelve) ways, choosing only two letters at a time from the four given.

Solution:
Possible lines are \(\overleftrightarrow { AB }\), \(\overleftrightarrow { AC }\), \(\overleftrightarrow { AD }\), \(\overleftrightarrow { BC }\), \(\overleftrightarrow { BD }\), \(\overleftrightarrow { CD }\), \(\overleftrightarrow { BA }\), \(\overleftrightarrow { CA }\), \(\overleftrightarrow { DA }\), \(\overleftrightarrow { CB }\), \(\overleftrightarrow { DB }\), \(\overleftrightarrow { DC }\).

Question 3.
Use the figure to name :

(a) Line containing point E.
(b) Line passing through A.
(c) Line on which O lies
(d) Two pairs of intersecting lines.
Solution:
(a) A line containing point E is \(\overleftrightarrow { AE }\).
(b) A line passing through A is \(\overleftrightarrow { AE }\).
(c) A line on which O lies is \(\overleftrightarrow { CO }\) or \(\overleftrightarrow { OC }\).
(d) Two pairs of intersecting lines are \(\overleftrightarrow { AD }\), \(\overleftrightarrow { CO }\) and \(\overleftrightarrow { AE }\), \(\overleftrightarrow { FE }\).

Question 4.
How many lines can pass through
(a) one given point?
(b) two given points?
Solution:
(a) Infinite number of lines can pass through one given point.

(b) Only one line can pass through two given points.

Question 5.
Draw a rough figure and label suitably in each of the following cases:
(a) Point Plies on \(\overline{A B}\).
(b) \(\overleftrightarrow { XY }\) and \(\overleftrightarrow { PQ }\) intersect at M.
(c) Line l contains E and F but not D.
(d) \(\overleftrightarrow { OP }\) and \(\overleftrightarrow { OQ }\) meet at O.
Solution:

Question 6.
Consider the following figure of line \(\overleftrightarrow { MN }\). Say whether following statements are true or false in context of the given figure.

(a) Q, M, O, N, P are points on the line \(\overleftrightarrow { MN }\).
(b) M, O, N are points on a line segment \(\overline{M N}\).
(c) M and N are end points of line segment \(\overline{M N}\).
(d) O and N are end points of line segment \(\overline{O P}\).
(e) M is one of the end points of line segment \(\overline{Q O}\).
(f) M is point on ray \(\overrightarrow { OP }\)
(g) Ray \(\overrightarrow { OP }\) is different from ray \(\overrightarrow { OP }\).
(h) Ray OP is same as ray \(\overrightarrow { OM }\).
(i) Ray \(\overrightarrow { OM }\) is not opposite to ray \(\overrightarrow { OP }\).
(j) O is not an initial point of \(\overrightarrow { OP }\).
(k) N is the initial point of \(\overrightarrow { NP }\) and \(\overrightarrow { NM }\).
Solution:
(a) True
(b) True
(c) True
(d) False
(e) False
(f) False
(g) True
(h) False
(i) False
(j) False
(k) True

MP Board Class 6th Maths Solutions

MP Board Class 6th Maths Solutions Chapter 12 Ratio and Proportion Ex 12.3

Question 1.
If the cost of 7 m of cloth is Rs. 294, find the cost of 5 m of cloth.
Solution:
Cost of 7 m of cloth = Rs. 294
∴ Cost of 1 m of cloth = Rs. \(\frac{294}{7}\) = Rs. 42
∴ Cost of 5 m of cloth = Rs. 42 × 5 = Rs. 210
Thus, the cost of 5 m of cloth is Rs. 210.

Question 2.
Ekta earns Rs. 1500 in 10 days. How much will she earn in 30 days?
Solution:
Earning of 10 days = Rs. 1500
∴ Earning of 1 day = Rs. \(\frac{1500}{10}\) = Rs.150
∴ Earning of 30 days = Rs. 150 × 30 = Rs. 4500
Thus, the earning of 30 days is Rs. 4,500.

Question 3.
If it has rained 276 mm in the last 3 days, how many cm of rain will fall in one full week (7 days)? Assume that the rain continues to fall at the same rate.
Solution:
Rain fall in 3 days = 276 mm 276
∴ Rain fall in 1 day = \(\frac{276}{3}\) mm = 92 mm
∴ Rain fall in 7 days = 92 × 7 mm = 644 mm
Thus, the rain fall in one full week is 644 mm.

Question 4.
Cost of 5 kg of wheat is Rs. 30.50.
(a) What will be the cost of 8 kg of wheat?
(b) What quantity of wheat can be purchased in Rs. 61?
Solution:
(a) Cost of 5 kg of wheat = Rs. 30.50
∴ Cost of 1 kg of wheat = Rs. \(\frac{30.50}{5}\) = Rs. \(\frac{3050}{500}\)
= Rs. 6.10
∴ Cost of 8 kg of wheat = Rs. 6.10 × 8 = Rs. 48.80

(b) From Rs. 30.50, quantity of wheat can be purchased = 5 kg
∴ From Re. 1, quantity of wheat can be purchased = \(\frac{5}{30.50}\) kg
∴ From Rs. 61, quantity of wheat can be purchased = \(\frac{5}{30.50}\) × 61 kg
= \(\frac{5}{3050}\) × 6100 kg = 10 kg

Question 5.
The temperature dropped 15 degree Celsius in the last 30 days. If the rate of temperature drop remains the same, how many degrees will the temperature drop in the next ten days?
Solution:
Temperature dropped in last 30 days = 15 degrees
∴ Temperature dropped in 1 day
= \(\frac{15}{30}\) degree = \(\frac{1}{2}\) degree
∴ Temperature will drop in next 10 days
= \(\frac{1}{2}\) × 10 degrees = 5 degrees
Thus, 5 degree Celsius temperature will drop in next 10 days.

Question 6.
Shaina pays Rs. 7500 as rent for 3 months. How much does she has to pay for a whole year, if the rent per month remains same?
Solution:
Rent paid for 3 months = Rs. 7500
∴ Rent paid for 1 month = Rs. \(\frac{7500}{3}\)
= Rs. 2500
∴ Rent paid for 12 months = Rs. 2500 × 12
= Rs. 30,000
Thus, the total rent of one year is Rs. 30,000.

Question 7.
Cost of 4 dozens bananas is Rs. 60. How many bananas can be purchased for Rs. 12.50?
Solution:
Cost of 4 dozens bananas = Rs. 60
i.e., cost of 48 bananas = Rs. 60 [∵ 4 dozens = 4 × 12 = 48]
From Rs. 60, number of bananas can be purchased = 48
∴ From Re. 1, number of bananas can be purchased = \(\frac{48}{60}=\frac{4}{5}\)
∴ FromRs. 12.50, number of bananas can be purchased
= \(\frac{4}{5}\) × 12.50 = \(\frac{4}{5} \times \frac{1250}{100}=\frac{250}{25}\) = 10
Thus, 10 bananas can be purchased for Rs. 12.50.

Question 8.
The weight of 72 books is 9 kg. What is the weight of 40 such books?
Solution:
The weight of 72 books = 9 kg
∴ The weight of 1 book = \(\frac{9}{72}\) kg = \(\frac{1}{8}\) kg
∴ The weight of 40 books = \(\frac{1}{8}\) × 40 kg = 5 kg
Thus, the weight of 40 books is 5 kg.

Question 9.
A truck requires 108 litres of diesel for covering a distance of 594 km. How much diesel will be required by the truck to cover a distance of 1650 km?
Solution:
For covering 594 km, required diesel = 108 litres
∴ For covering 1 km, required diesel
= \(\frac{108}{594}\) litres = \(\frac{2}{11}\) litres
∴ For covering 1650 km, required diesel
= \(\frac{2}{11}\) × 1650 litres = 300 litres
Thus, 300 litres of diesel will be required by the truck to cover a distance of 1650 km.

Question 10.
Raju purchases 10 pens for Rs. 150 and Manish buys 7 pens for Rs. 84. Can you say who got the pens cheaper?
Solution:
Cost of 10 pens for Raju = Rs. 150
∴ Cost of 1 pen for Raju = Rs. \(\frac{150}{10}\) = Rs. 15
Cost of 7 pens for Manish = Rs. 84
∴ Cost of 1 pen for Manish = Rs. \(\frac{84}{7}\) = Rs. 12
Thus, Manish got the pens cheaper.

Question 11.
Anish made 42 runs in 6 overs and Anup made 63 runs in 7 overs. Who made more runs per over?
Solution;
Runs made by Anish in 6 overs = 42
∴ Runs made by Anish in 1 over = \(\frac{42}{6}\) = 7
Runs made by Anup in 7 overs = 63
∴ Runs made by Anup in 1 over = \(\frac{63}{7}\) = 9
Thus, Anup made more runs per over.

MP Board Class 6th Maths Solutions

MP Board Class 6th Maths Solutions Chapter 12 Ratio and Proportion Ex 12.2

Question 1.
Determine if the following are in proportion.
(a) 15, 45, 40, 120
(b) 33, 121, 9, 96
(c) 24, 28, 36, 48
(d) 32, 48, 70, 210
(e) 4, 6, 8, 12
(f) 33, 44, 75, 100
Solution:

Question 2.
Write True (T) or False (F) against each of the following statements:
(a) 16 : 24 :: 20 : 30
(b) 21 : 6 :: 35 : 10
(c) 12 : 18 :: 28 : 12
(d) 8 : 9 :: 24 : 27
(e) 5.2 : 3.9 :: 3 : 4
(f) 0.9 : 0.36 :: 10 : 4
Solution:
(a) True

Question 3.
Are the following statements true?
(a) 40 persons : 200 persons = Rs. 15 : Rs. 75
(b) 7.5 litres: 15 litres = 5 kg : 10 kg
(c) 99 kg : 45 kg = Rs. 44 : Rs. 20
(d) 32 m: 64 m = 6 sec : 12 sec
(e) 45 km : 60 km = 12 hours : 15 hours
Solution:
(a) 40 persons : 200 persons

∴ 40 persons : 200 persons = Rs. 15 : Rs. 75
Hence, the statement is true.

Question 4.
Determine if the following ratios form a proportion. Also, write the middle terms and extreme terms where the ratios form a proportion.
(a) 25 cm : 1 m and Rs. 40: Rs. 160
(b) 39 litres: 65 litres and 6 bottles: 10 bottles
(c) 2 kg : 80 kg and 25 g : 625 g
(d) 200 ml: 2.5 litre and Rs. 4: Rs. 50
Solution:
(a) 25 cm : 1 m = 25 cm : (1 × 100) cm

Since the ratios are equal, therefore these are in proportion.
Middle terms are 1 m and Rs. 40 and extreme terms are 25 cm and Rs. 160.

Since the ratios are equal, therefore these are in proportion.
Middle terms are 65 litres and 6 bottles and extreme terms are 39 litres and 10 bottles.

Since the ratios are not equal, therefore these are not in proportion.
(d) 200 ml : 2.5 litres = 200 ml: (2.5 × 1000) ml

Since the ratios are equal, therefore these are in proportion.
Middle terms are 2.5 litres and Rs. 4 and extreme terms are 200 ml and Rs. 50.

MP Board Class 6th Maths Solutions

MP Board Class 6th Maths Solutions Chapter 3 Playing With Numbers Ex 3.7

Question 1.
Renu purchases two bags of fertiliser of weights 75 kg and 69 kg. Find the maximum value of weight which can measure the weight of the fertiliser exact number of times.
Solution:
For finding maximum weight, we have to find HCF of 75 and 69.
The prime factorisation of 75 and 69 are;
75 = 3 × 5 × 5
69 = 3 × 23
So, HCF of 75 and 69 = 3
Therefore, the required weight is 3 kg.

Question 2.
Three boys step off together from the same spot. Their steps measure 63 cm, 70 cm and 77 cm respectively. What is the minimum distance each should cover so that all can cover the distance in complete steps?
Solution:
For finding minimum distance, we have to find LCM of 63, 70, 77.

L.C.M. of 63, 70 and 77 = 2 × 3 × 3 × 5 × 7 × 11
= 6930
Therefore, the minimum distance three boys should cover is 6930 cm.

Question 3.
The length, breadth and height of a room are 825 cm, 675 cm and 450 cm respectively. Find the longest tape which can measure the three dimensions of the room exactly.
Solution:
The measurement of the longest tape = HCF of 825 cm, 675 cm and 450 cm are;
825 = 3 × 5 × 5 × 11
675 = 3 × 3 × 3 × 5 × 5
450 = 2 × 3 × 3 × 5 × 5
Now, HCF of 825, 675 and 450 = 3 × 5 × 5 = 75
Therefore, the measurement of longest tape is 75 cm

Question 4.
Determine the smallest 3-digit number which is exactly divisible by 6, 8 and 12.
Solution:
The smallest 3-digit number = 100

L.C.M of 6, 8 and 12 = 2 × 2 × 2 × 3 = 24
To find the number, we have to divide 100 by 24.

Therefore, the required number = 100 + (24 – 4) = 120.

Question 5.
Determine the greatest 3-digit number exactly divisible by 8,10 and 12.
Solution:
The greatest three digit number = 999.

L.C.M of 8, 10 and 12 = 2 × 2 × 2 × 3 × 5 = 120
Now, to find the number, we have to divide 999 by 120.

Therefore the required number = 999 – 39 = 960

Question 6.
The traffic lights at three different road crossings change after every 48 seconds, 72 seconds and 108 seconds respectively. If they change simultaneously at 7 a.m., at what time will they change simultaneously again?
Solution:

LCM of 48, 72 and 108 = 2 × 2 × 2 × 2 × 3 × 3 × 3 = 432
After 432 seconds, the traffic lights change simultaneously.
432 seconds = 7 minutes 12 seconds
Therefore, the required time = 7 a.m. + 7 minutes 12 seconds i.e., 7 minutes 12 seconds past 7 a.m.

Question 7.
Three tankers contain 403 litres, 434 litres and 465 litres of diesel respectively. Find the maximum capacity of a container that can measure the diesel of the three containers exact number of times.
Solution:
The maximum capacity of a container = HCF (403, 434, 465)
The prime factorisation of 403, 434 and 465 are;
403 = 13 × 31
434 = 2 × 7 × 31
465 = 3 × 5 × 31
HCF of 403, 434, 465 = 31
Therefore, a container of capacity 31 litres is required to measure the diesel of the three containers.

Question 8.
Find the least number which when divided by 6,15 and 18 leave remainder 5 in each case.
Solution:

LCM of 6,15 and 18 = 2 × 3 × 3 × 5 = 90
Therefore, the required number = 90 + 5 = 95

Question 9.
Find the smallest 4-digit number which is divisible by 18, 24 and 32.
Solution:
The smallest four digit number = 1000

LCM of 18, 24 and 32 = 2 × 2 × 2 × 2 × 2 × 3 × 3 = 288
Now,

Therefore, the required number is 1000 + (288 – 136) = 1152.

Question 10.
Find the LCM of the following numbers :
(a) 9 and 4
(b) 12 and 5
(c) 6 and 5
(d) 15 and 4
Observe a common property in the obtained LCMs. Is LCM the product of two numbers in each case?
Solution:
(a) We have,

LCM of 9 and 4 = 2 × 2 × 3 × 3 = 36

(b) We have,

LCM of 12 and 5 = 2 × 2 × 3 × 5 = 60

(c) We have,

LCM of 6 and 5 = 2 × 3 × 5 = 30

(d) We have,

LCM of 15 and 4 = 2 × 2 × 3 × 5 = 60
Yes, the LCM is equal to the product of two numbers in each case and all LCMs are also the multiple of 3.

Question 11.
Find the LCM of the following numbers in
(a) 5, 20
(b) 6, 18
(c) 12, 48
(d) 9, 45
What do you observe in the results obtained?
Solution:
(a) We have,

LCM of 5 and 20 = 2 × 2 × 5 = 20

(b) We have

LCM of 6 and 18 = 2 × 3 × 3 = 18

(c) We have

LCM of 12 and 48 = 2 × 2 × 2 × 2 × 3 = 48

(d) We have

LCM of 9 and 45 = 3 × 3 × 5 = 45
From above, we observe that the LCM of the given numbers in each case is the larger of the two numbers.

MP Board Class 6th Maths Solutions

MP Board Class 6th Maths Solutions Chapter 12 Ratio and Proportion Ex 12.1

Question 1.
There are 20 girls and 15 boys in a class.
(a) What is the ratio of number of girls to the number of boys?
(b) What is the ratio of number of girls to the total number of students in the class?
Solution:
(a) The ratio of number of girls to that of boys = \(\frac{20}{15}=\frac{4}{3}\) = 4 : 3
(b) The ratio of number of girls to total number of students = \(\frac{20}{20+15}=\frac{20}{35}=\frac{4}{7}\) = 4 : 7

Question 2.
Out of 30 students in a class, 6 like football, 12 like cricket and remaining like tennis. Find the ratio of
(a) Number of students liking football to number of students liking tennis.
(b) Number of students liking cricket to total number of students.
Solution:
Total number of students = 30
Number of students like football = 6
Number of students like cricket = 12
Thus, number of students like tennis = 30 – 6 – 12 = 12
(a) The ratio of number of students liking football to that of tennis = \(\frac{6}{12}=\frac{1}{2}\) = 1 : 2
(b) The ratio of number of students liking cricket to that of total students = \(\frac{12}{30}=\frac{2}{5}\) = 2 : 5

Question 3.
See the figure and find the ratio of
(a) Number of triangles to the number of circles inside the rectangle.
(b) Number of squares to all the figures inside the rectangle.
(c) Number of circles to all the figures inside the rectangle.

Solution:
(a) The ratio of number of triangles to that of circles = \(\frac{3}{2}\) = 3 : 2
(b) The ratio of number of squares to that of all figures = \(\frac{2}{7}\) = 2 : 7
(c) The ratio of number of circles to that of all figures = \(\frac{2}{7}\) = 2 : 7

Question 4.
Distances travelled by Hamid and Akhtar in an hour are 9 km and 12 km. Find the ratio of speed of Hamid to the speed of Akhtar.
Solution:

Question 5.
Fill in the following blanks :

Solution:
In order to get the first missing number, we consider the fact that 18 = 3 × 6, i.e., we get 6 when we divide 18 by 3. This indicates that to get the missing number of the second ratio, 15 must also be divided by 3.
When we divide, we get 15 – 5 – 3 = 5. Hence, the second ratio is \(\frac{5}{6}\) .
Similarly, to get the third ratio, we multiply both terms of the second ratio by 2. Hence, the third ratio is \(\frac{10}{12}\).
And to get the fourth ratio, we multiply both terms of the second ratio by 5. Hence, the fourth ratio is \(\frac{25}{30}\).

Yes, these are equivalent ratios.

Question 6.
Find the ratio of the following :
(a) 81 to 108
(b) 98 to 63
(c) 33 km to 121 km
(d) 30 minutes to 45 minutes
Solution:
(a) The ratio of 81 to 108

Question 7.
Find the ratio of the following:
(a) 30 minutes to 1.5 hours
(b) 40 cm to 1.5 m
(c) 55 paise to Re. 1
(d) 500 ml to 2 litres
Solution:
(a) 1.5 hours = 1.5 × 60 minutes
= 90 minutes [ ∵ 1 hour = 60 minutes]
Now, the ratio of 30 minutes to 1.5 hours = 30 minutes : 1.5 hours
= 30 minutes: 90 minutes = \(\frac{30}{90}=\frac{1}{3}\) = 1 : 3

(b) 1.5 m = 1.5 × 100 cm = 150 cm [∵ 1 m = 100 cm]
Now, the ratio of 40 cm to 1.5 m = 40 cm : 1.5 m
= 40 cm : 150 cm = \(\frac{40}{150}=\frac{4}{15}\) = 4 : 15

(c) Re. 1 = 100 paise
Now, the ratio of 55 paise to Re. 1
= 55 paise : Re. 1 = 55 paise : 100 paise
= \(\frac{55}{100}=\frac{11}{20}\) = 11 : 20

(d) 2 litres = 2 × 1000 ml = 2000 ml [∵ 1 litre = 1000 ml]
Now, the ratio of 500 ml to 2 litres = 500 ml : 2 litres
= 500 ml : 2000 ml = \(\frac{500}{2000}=\frac{1}{4}\) = 1 : 4

Question 8.
In a year, Seema earns Rs. 1,50,000 and saves Rs. 50,000. Find the ratio of
(a) Money that Seema earns to the money she saves.
(b) Money that she saves to the money she spends.
Solution:
Total earning of Seema = Rs. 1,50,000 and savings = Rs. 50,000
∴ Money spent by her
= Rs. 1,50,000 – Rs. 50,000 = Rs. 1,00,000
(a) The ratio of money earned to the money saved by Seema = \(\frac{150000}{50000}=\frac{3}{1}\) = 3 : 1
(b) The ratio of money saved to the money spent by Seema = \(\frac{50000}{100000}=\frac{1}{2}\) = 1 : 2

Question 9.
There are 102 teachers in a school of 3300 students. Find the ratio of the number of teachers to the number of students.
Solution:
The ratio of number of teachers to that of students = \(\frac{102}{3300}=\frac{17}{550}\) = 17 : 550

Question 10.
In a college, out of 4320 students, 2300 are girls. Find the ratio of
(a) Number of girls to the total number of students.
(b) Number of boys to the number of girls.
(c) Number of boys to the total number of students.
Solution:
Total number of students in the college = 4320
Number of girls = 2300
Therefore, number of boys = 4320 – 2300
= 2020

Question 11.
Out of 1800 students in a school, 750 opted basketball, 800 opted cricket and remaining opted table tennis. If a student can opt only one game, find the ratio of
(a) Number of students who opted basketball to the number of students who opted table tennis.
(b) Number of students who opted cricket to the number of students opting basketball.
(c) Number of students who opted basketball to the total number of students.
Solution:
Total number of students = 1800 Number of students who opted basketball = 750
Number of students who opted cricket = 800 Therefore, number of students who opted table tennis = 1800 – (750 + 800) = 250
(a) The ratio of number of students who opted basketball to that who opted table tennis

(b) The ratio of number of students who opted cricket to that who opted basketball

(c) The ratio of number of students who opted basketball to the total number of students

Question 12.
Cost of a dozen pens is Rs. 180 and cost of 8 ball pens is Rs. 56. Find the ratio of the cost of a pen to the cost of a ball pen.
Solution:
Cost of a dozen pens (12 pens) = Rs. 180
∴ Cost of 1 pen = Rs. \(\frac{180}{12}\)= Rs. 15
Cost of 8 ball pens = Rs. 56
∴ Cost of 1 ball pen = Rs. \(\frac{56}{8}\) = Rs. 7
Hence, the ratio of cost of one pen to that of one ball pen = \(\frac{15}{7}\) = 15 : 7

Question 13.
Consider the statement: Ratio of breadth and length of a hall is 2 :5. Complete the following table that shows some possible breadths and lengths of the hall.

Solution:
Ratio of breadth to length of the ball = 2 : 5 = \(\frac{2}{5}\)
∴ Other equivalent ratios are

Question 14.
Divide 20 pens between Sheela and Sangeeta in the ratio of 3 : 2.
Solution:
The ratio of dividing pens between Sheela and Sangeeta = 3 : 2.
∴ The two parts are 3 and 2.
Sum of the parts = 3 + 2 = 5

Question 15.
Mother wants to divide Rs. 36 between her daughters Shreya and Bhoomika in the ratio of their ages. If age of Shreya is 15 years and age of Bhoomika is 12 years, find how much Shreya and Bhoomika will get.
Solution:
The ratio of the age of Shreya to that of
Bhoomika = \(\frac{15}{12}=\frac{5}{4}\) = 5 : 4
Thus, Rs. 36 will be divided between Shreya and Bhoomika in the ratio of 5 : 4.

Question 16.
Present age of father is 42 years and that of his son is 14 years. Find the ratio of
(a) Present age of father to the present age of son.
(b) Age of the father to the age of son, when son was 12 years old.
(c) Age of father after 10 years to the age of son after 10 years.
(d) Age of father to the age of son when father was 30 years old.
Solution:
(a) The ratio of father’s present age to that of son = \(\frac{42}{14}=\frac{3}{1}\) = 3 : 1

(b) When son was 12 years old, i.e., 2 years ago, then father was (42 – 2) = 40 years old.
Therefore, the required ratio of their ages = \(\frac{40}{12}=\frac{10}{3}\) = 10 : 3

(c) Age of father after 10 years = (42 + 10) years = 52 years
Age of son after 10 years = (14 + 10) years = 24 years
Therefore, the required ratio of their ages = \(\frac{52}{24}=\frac{13}{6}\) = 13 : 6

(d) When father was 30 years old, i.e., 12 years ago, then son was (14 – 12) = 2 years old.
Therefore, the required ratio of their ages = \(\frac{30}{2}=\frac{15}{1}\) = 15 : 1

MP Board Class 6th Maths Solutions

MP Board Class 6th Maths Solutions Chapter 13 Symmetry Ex 13.3

Question 1.
Find the number of lines of symmetry in each of the following shapes. How will you check your answers?
content/uploads/2020/10/MP-Board-Class-6th-Maths-Solutions-Chapter-13-Symmetry-Ex-13.3-1.png” alt=”MP Board Class 6th Maths Solutions Chapter 13 Symmetry Ex 13.3 1″ width=”305″ height=”256″ />
Solution:
(a) Number of lines of symmetry = 4.

(b) Number of lines of symmetry = 1.

(c) Number of lines of symmetry = 2.

(d) Number of lines of symmetry = 2.

(e) Number of lines of symmetry = 1.

(f) Number of lines of symmetry = 2.

Question 2.
Copy the following drawing on squared paper. Complete each one of them such that the resulting figure has two dotted lines as two lines of symmetry.

Solution:

Question 3.
In each figure alongside, a letter of the alphabet is shown along with a vertical line. Take the mirror image of the letter in the given line. Find which letters look the same after reflection (i.e. which letters look the same in the image) and which do not. Can you guess why?
Try for O E M N P H L T S V X

Solution:


Letters which look the same after reflection are A, O, M, H, T, V, X and which do not look the same after reflection are B, E, N, P, L, S.

MP Board Class 6th Maths Solutions

MP Board Class 6th Maths Solutions Chapter 13 Symmetry Ex 13.2

Question 1.
Find the number of lines of symmetry for each of the following shapes:


Solution:
(a)

Lines of symmetry are AB, CD, EF and GH.
∴ Number of lines of symmetry = 4

(b)

Lines of symmetry are AB, CD, EF and GH.
∴ Number of lines of symmetry = 4

(c)

Lines of symmetry are AB, CD, EF and GH.
∴ Number of lines of symmetry = 4

(d)

Lines of symmetry is AB.
∴ Number of lines of symmetry = 1

(e)

Lines of symmetry are AB, CD, EF, GH, IJ and KL.
∴ Number of lines of symmetry = 6

(f)

Lines of symmetry are AB, CD, EF, GH, IJ and KL.
∴ Number of lines of symmetry = 6
(g) No lines of symmetry.
(h) No lines of symmetry.
(i)

Lines of symmetry are AB, CD, EF, GH and IJ.
∴ Number of lines of symmetry = 5

Question 2.
Copy the triangle in each of the following figures on squared paper. In each case, draw the line(s) of symmetry, if any and identify the type of triangle. (Some of you may like to trace the figures and try paper-folding first!)

Solution:

Question 3.
Complete the following table.


Solution

Question 4.
Can you draw a triangle which has
(a) exactly one line of symmetry?
(b) exactly two lines of symmetry?
(c) exactly three lines of symmetry?
(d) no lines of symmetry?
Sketch a rough figure in each case.
Solution:
(a) Yes, an isosceles triangle has one line of symmetry

(b) No, triangle cannot be formed which has exactly two lines of symmetry.
(c) Yes, equilateral triangle has three lines of symmetry.

(d) Yes, scalene triangle has no lines of symmetry.

Question 5.
On a squared paper, sketch the following:
(a) A triangle with a horizontal line of symmetry but no vertical line of symmetry.
(b) A quadrilateral with both horizontal and vertical lines of symmetry.
(c) A quadrilateral with a horizontal line of symmetry but no vertical line of symmetry.
(d) A hexagon with exactly two lines of symmetry.
(e) A hexagon with six lines of symmetry.
(Hint: It will be helpful if you first draw the lines of symmetry and then complete the figures.)
Solution:

Question 6.
Trace each figure and draw the lines of symmetry, if any:

Solution:

Question7.
Consider the letters of English alphabets, A to Z. List among them the letters which have
(a) vertical lines of symmetry (like A)
(b) horizontal lines of symmetry (like B)
(c) no lines of symmetry (like Q)

Solution:
(a) The letters which have vertical lines of symmetry are A, H, I, M, O, T, U, V, W, X, Y.
(b) The letters which have horizontal lines of symmetry are B, C, D, E, H, I, K, O, X.
(c) The letters which have no line of symmetry are F, G, J, L, N, P, Q, R, S, Z

Question 8.
Given here are figures of a few folded sheets and designs drawn about the fold. In each case, draw a rough diagram of the complete figure that would be seen when the design is cut off.

Solution:

MP Board Class 6th Maths Solutions

MP Board Class 6th Social Science Solutions Chapter 5 The Solar System and Our Earth

MP Board Class 6th Social Science Chapter 5 Text Book Exercise

MP Board Class 6th Social Science Chapter 5 Short Answer Type Questions

Question 1.
Question (a)
How does the sun get energy?
Answer:
The sun is burning like a big atomic power plant. The studies of scientists have shown that the sun is a burning body of inflammable gases in which hydrogen, helium and other gases bum and react continuously, producing heat and life for millions of years.

Question (b)
What are the three realms of earth?
Answer:
The three realms of earth are lithosphere, atmosphere and hydrosphere.

Question (c)
Explain the importance of the sun?
Answer:
Sun is the head of the solar system. It is situated in the centre of the solar system. All the planets, the satellites the asteroids, the meteorites and the comets revolve round the sun. All these members get light and energy from the sun. About 99% part of all the matter in the Solar System is constitute in the sun. The sun is so big that all the planets together would cover only 1% of it.

The sun has tremendous force of gravity due to its such a large sizes. It is due to the gravitational force that all the planets and the satellites regularly rotate round it. The sun is a big ball of fire. It is also a storehouse of light and energy. Our earth gets light and energy from the sun. Day occurs on earth due to the light from the sun.

Question (d)
Write the names of the planets in the solar system?
Answer:
The Sun and the nine planets which revolve around it make up the ‘Family of the Sun’ Solar System.

The Solar System consists of the Sun as the centre and Mercury, Venus, Earth, Mars, Jupiter, Saturn, Uranus, Neptune and Pluto as planets. In addition, there are in all 44 satellites in our Solar System.

Question (e)
Write the difference between planets and stars?
Answer:
Difference between star and planet:

Planet:

1. A planet is a celestial body that revolves round the sun.
2. There are nine planets in our Solar System. They do not have their own heat or light.
3. Planets draw their light and energy from sun.
4. They are nine in number, including our earth.
5. The earth is an example of a planet.

Star:

1. A star is also a celestial body and is a part of galaxy.
2. There are numerous stars in a galaxy. Each star may have a family of planets.
3. A star has its own light and heat.
4. They are guite large (in billions) in number.
5. The sun is an example of a star.

Question (f)
Which is the life saving gas?
Answer:
Ozone is the life saving gas.

Question (g)
Name three important gases found on earth, which is the life giving gas among them?
Answer:
The three important gases found on earth are Oxygen, Nitrogen and Carbondioxide. Oxygen is the life giving gas.

Question (h)
What is the difference between planets and statellites?
Answer:
Difference between Planet and Satellite.

Planet:

1. Roughly a planet has a spherical body.
2. It revolves round the sun in an elliptical path known as its orbit.
3. There are nine major planets.
4. The word ‘planet’ means wanderer.
5. The Earth is its good example.

Satellite:

1. A satellite has a relatively small body.
2. It revolves round its planet.
3. There are in all thirty – two satellites.
4. The word (satellite) means’companion’ or ‘attendant.’
5. The Moon is its good example. It is a satellite of the Eart

MP Board Class 6th Social Science Chapter 5 Long Answer Type Questions

Question 2.
Question (a)
What is Solar System? Make a labelled diagram of the Solar System?
Answer:
The Sun and the nine planets which revolve around it make up the family of the Sun or the Solar System. In addition to the nine planets, there are 44 satellites in the Solar System.

Question (b)
How is the earth a unique and living planet? Explain.
Answer:
The earth is a small member of the Solar System. It is the fifth in size of the nine major planets and the third in distance. But it occupies a very unique position in the Solar System, for the following reasons:

1.  Around the Earth is a gaseous envelope known as the atmosphere. It saves us from the extreme heat of the Sun.

2. The Earth has land, water and air unlike the other planets which makes life possible. All this had made the Earth a sweet home for us.

Question (c)
What are natural and artificial satellites? Describe the natural satellite of the earth.
Answer:
1. The celestial bodies that rotate round a planet are called satellites or natural satellites. The satellites also get light and heat from the sun. Incept the Venus and the Mars, all planets have their own satellites.

2. There are other satellites than the natural satellite which are man made. They are called the artificial satellites. The Indian scientist have sent some artificial satellites into the space. The first such satellite was the Arybhatta.

3. The other artificial satellites are the Rohini, Bhaskar, Apple, etc. They provide us a information system giving weather forecast, telecast, radio broadcast, telecommunication, information to improve agriculture and in-formation regarding minerals, etc.

4. The Moon is the only natural satellite of our planet. The moon moves around the earth and also around the sun along with the earth.The moon has rugged and barren surface. There is no air or water on the moon. It is very, hot during the day and very cold during the night.

Question 3.
Give one term for the following sentences:

1. An infinite system of all matter, all galaxies, all energy and space.
2. The distance travelled by light in one year with a velocity of three lakh kilometres per second.
3. The milky band seen on a clear starlit night.
4. A band of innumerable tiny bodies between Mars and Jupiter in the solar system.

Answer:

1. The Universe
2. Light – year
3. Galaxy or Akash Ganga
4. Asteroids

Question 4.

Match the columns :

Answer:

Project Work

Question 1.
Draw a big diagram of the solar system. Label it?
Answer:
The Sun and the nine planets which revolve around it make up the family of the Sun or the Solar System. In addition to the nine planets, there are 44 satellites in the Solar System.

MP Board Class 6th Social Science Solutions

MP Board Class 6th Maths Solutions Chapter 3 Playing With Numbers Ex 3.6

Question 1.
Find the HCF of the following numbers :
(a) 18, 48
(c) 18, 60
(e) 36, 84
(g) 70, 105, 175
(i) 18,54,81
Solution:
(a) The prime factorisation of 18 and
48 are; 18 = 2 × 3 × 3
48 = 2 × 2 × 2 × 2 × 3
∴ HCF (18, 48) = 2 × 3 = 6

(b) The prime factorisation of 30 and 42 are; 30 = 2 × 3 × 5
42 = 2 × 3 × 7
∴ HCF (30, 42) = 2 * 3 = 6

(c) The prime factorisation of 18 and 60 are; 18 = 2 × 3 × 3
60 = 2 × 2 × 3 × 5
∴ HCF (18, 60) = 2 × 3 = 6

(d) The prime factorisation of 27 and 63 are; 27 = 3 × 3 × 3
63 = 3 × 3 × 7
HCF (27, 63) = 3 × 3 = 9

(e) The prime factorisation of 36 and 84 are; 36 = 2 × 2 × 3 × 3
84 = 2 × 2 × 3 × 7
HCF (36, 84) = 2 × 2 × 3 = 12

(f) The prime factorisation of 34 and 102 are; 34 = 2 × 17
102 = 2 × 3 × 17
HCF (34, 102) = 2 × 17 = 34

(g) The prime factorisation of 70, 105 and 175 are; 70 = 2 × 5 × 7
105 = 3 × 5 × 7
175 = 5 × 5 × 7
HCF (70, 105, 175) = 5 × 7 = 35

(h) The prime factorisation of 91, 112 and 49 are; 91 = 7 × 13
112 = 2 × 2 × 2 × 2 × 7
49 = 7 × 7
∴ HCF (91, 112, 49) = 7

(i) The prime factorisation of 18, 54 and 81 are; 18 = 2 × 3 × 3
54 = 2 × 3 × 3 × 3
81 = 3 × 3 × 3 × 3
HCF (18, 54, 81) = 3 × 3 = 9

(j) The prime factorisation of 12, 45 and 75 are; 12 = 2 × 2 × 3
45 = 3 × 3 × 5
75 = 3 × 5 × 5
∴ HCF (12, 45, 75) = 3

Question 2.
What is the HCF of two consecutive
(a) numbers?
(b) even numbers?
(c) odd numbers?
Solution:
(a) HCF of two consecutive numbers is 1.
(b) HCF of two consecutive even numbers is 2.
(c) HCF of two consecutive odd numbers is 1.

Question 3.
HCF of co-prime numbers 4 and 15 was found as follows by factorisation :
4 = 2 × 2 and 15 = 3 × 5 since there is no common prime factor, so HCF of 4 and 15 is 0. Is the answer correct? If not, what is the correct HCF?
Solution:
No. The correct HCF of 4 and 15 is 1.

MP Board Class 6th Maths Solutions