MP Board Class 6th Maths Solutions Chapter 11 बीजगणित Ex 11.4
पाठ्य-पुस्तक पृष्ठ संख्या # 255-256
प्रश्न 1.
निम्नलिखित प्रश्नों के उत्तर दीजिए :
(a) सरिता की वर्तमान आयु y वर्ष लीजिए।
(i) आज से 5 वर्ष बाद उसकी आयु क्या होगी ?
(ii) 3 वर्ष पहले उसकी आयु क्या थी?
(iii) सरिता के दादाजी की आयु उसकी आयु की 6 गुनी है। उसके दादाजी की क्या आयु है ?
(iv) उसकी दादीजी दादाजी से 2 वर्ष छोटी है। दादीजी की आयु क्या है ?
(v) सरिता के पिता की आयु सरिता की आयु के तीन गुने से 5 वर्ष अधिक है। उसके पिता की आयु क्या है ?
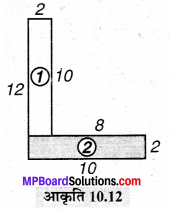
(b) एक आयताकार हॉल की लम्बाई उसकी चौड़ाई के तिगुने से 4 मीटर कम है। यदि चौड़ाई b मीटर है, तो लम्बाई क्या है ?
(c) एक आयताकार बक्स की चौड़ाई h सेमी है। इसकी लम्बाई, ऊँचाई की 5 गुनी है और चौड़ाई लम्बाई से 10 सेमी कम है। बक्स की लम्बाई और चौड़ाई को ऊँचाई के पदों में व्यक्त कीजिए।
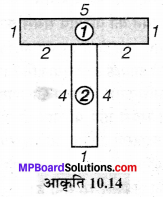
(d) मीना, बीना और लीना पहाड़ी की चोटी पर पहुँचने के लिए सीढ़ियाँ चढ़ रही हैं। मीना सीढ़ी s पर है। बीना मीना से 8 सीढ़ियाँ आगे है और लीना मीना से 7 सीढ़ियाँ पीछे है। बीना और लीना कहाँ पर हैं ? चोटी पर पहुँचने के लिए कुल सीढ़ियाँ मीना द्वारा चढ़ी गई सीढ़ियों की संख्या के चार गुने से 10 कम हैं। सीढ़ियों की कुल संख्या को s के पदों में व्यक्त कीजिए।
(e) एक बस v किमी प्रति घण्टा की चाल से चल रही है। यह दासपुर से बीसपुर जा रही है। बस के 5 घण्टे चलने के बाद भी बीसपुर 20 किमी दूर रह जाता है। दासपुर से बीसपुर की दूरी क्या है ? इसे v का प्रयोग करते हुए व्यक्त कीजिए।
उत्तर-
(a) (i) सरिता की वर्तमान आयु = y वर्ष
5 वर्ष बाद उसकी आयु = y + 5 वर्ष
(ii) 3 वर्ष पहले उसकी आयु = y – 3 वर्ष
(iii) दादाजी की आयु = 6 x सरिता की वर्तमान आयु
= 6y वर्ष
(iv) दादीजी की आयु = दादाजी की आयु – 2
= 6y – 2 वर्ष
(v) सरिता के पिता की आयु = 3 x सरिता की आयु + 5 वर्ष
= 3y + 5 वर्ष
(b) ∵ हॉल की चौड़ाई = b मीटर
लम्बाई = 3 x चौड़ाई – 4 मीटर
= 3b – 4 मीटर
(c) माना कि बक्स की ऊँचाई = h सेमी
∴ बक्स की लम्बाई = 5 x चौड़ाई = 5h सेमी
और बक्स की चौड़ाई = (लम्बाई – 10) सेमी
= (5h – 10) सेमी
(d) ∵ मीना सीढ़ी s पर है।
∴ बीना की स्थिति = s + 8 सीढ़ियाँ
और लीना की स्थिति = s – 7 सीढ़ियाँ
∴ चोटी पर पहुँचने के लिए कुल सीढ़ियाँ
= 4 x मीना द्वारा चढ़ी गई सीढ़ियों की संख्या – 10
= 4 x s – 10
= 4s – 10 सीढ़ियाँ
(e) बस की चाल = v किमी/घण्टा
5 घण्टे में चली गई दूरी = 5 x v किमी
= 5v किमी
∴ बीसपुर की दूरी = 5v + 20 किमी
अतः दासपुर से बीसपुर की दूरी = 5v + 20 किमी
![]()
प्रश्न 2.
व्यंजकों के प्रयोग से बने निम्न कथनों को साधारण भाषा के कथनों में बदलिए :
(उदाहरणार्थ, एक क्रिकेट मैच में सलीम ने r रन बनाए और नलिन ने (r + 15) रन बनाए। साधारण भाषा में, नलिन ने सलीम से 15 अधिक बनाए हैं।)
(a) एक अभ्यास पुस्तिका का मूल्य Rs p है। एक पुस्तक का मूल्य Rs 3p है।
(b) टोनी ने मेज पर q कंचे रखे। उसके पास डिब्बे में 8q कंचे हैं।
(c) हमारी कक्षा में n विद्यार्थी हैं। स्कूल में 20n विद्यार्थी हैं।
(d) जग्गू की आयु z वर्ष है। उसके चाचा की आयु 4z वर्ष है और उसकी चाची की आयु (4z – 3) वर्ष है।
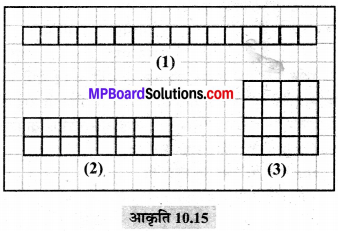
(e) बिन्दुओं (dots) की एक व्यवस्था में r पंक्तियाँ हैं। प्रत्येक पंक्ति में 5 बिन्दु हैं।
उत्तर-
(a) पुस्तक का मूल्य अभ्यास-पुस्तिका के मूल्य का तीन गुना है।
(b) टोनी के डिब्बे में मेज पर रखे कंचों के 8 गुने कंचे हैं।
(c) स्कूल के विद्यार्थियों की कुल संख्या हमारी कक्षा के विद्यार्थियों की बीस गुनी है।
(d) जग्गू के चाचा की आयु जग्गू की आयु की 4 गुनी है और जग्गू की चाची की आयु उसके चाचा से 3 वर्ष कम है।
(e) बिन्दुओं की संख्या पंक्तियों की संख्या की 5 गुनी है।
प्रश्न 3.
(a) मुन्नू की आयु x वर्ष दी हुई है। क्या आप अनुमान लगा सकते हैं कि (x – 2) क्या दर्शाएगा?
(संकेत : मुन्नू के छोटे भाई के बारे में सोचिए।) क्या आप अनुमान लगा सकते हैं कि (x + 4) क्या दर्शाएगा और 3x + 7 क्या दर्शाएगा?
(b) सारा की वर्तमान आयु y वर्ष दी हुई है। उसकी भविष्य की आयु और पिछली आयु के बारे में सोचिए। निम्नलिखित व्यंजक क्या सूचित करते हैं?
y + 7, y – 3, y + \(4\frac { 1 }{ 2 }\), y – \(2\frac { 1 }{ 2 }\)
(c) दिया हुआ है कि एक कक्षा के n विद्यार्थी फुटबॉल खेलना पसन्द करते हैं। 2n क्या दर्शाएगा? \(\frac { n }{ 2 }\) क्या दर्शा सकता है ? (संकेत : फुटबॉल के अतिरिक्त अन्य खेलों के बारे में सोचिए।)
उत्तर-
(a) (i) x – 2 सम्भवतः उसके छोटे भाई या बहन की आयु दर्शाएगा?
(ii) (x + 4) उसके बड़े भाई की आयु दर्शाएगा।
(iii) (3x + 7) उसकी माँ की आयु दर्शाएगा।
मुन्नू की माँ की आयु उसकी आयु के तीन गुने से 7 वर्ष अधिक है।
(b) (i) व्यंजक (y + 7)7 वर्ष बाद सारा की आयु दर्शाता है। व्यंजक (y – 3), 3 वर्ष पूर्व सारा की आयु दर्शाता है।
(ii) व्यंजक (y + \(4\frac { 1 }{ 2 }\)), \(4\frac { 1 }{ 2 }\) वर्ष पश्चात् सारा की उम्र दर्शाता है।
(iii) व्यंजक (y – \(2\frac { 1 }{ 2 }\)), \(2\frac { 1 }{ 2 }\) वर्ष पूर्व सारा की आयु दर्शाता है।
(c) चूँकि n विद्यार्थी फुटबॉल खेलना पसन्द करते हैं।
(i) ∴ 2n (फुटबॉल खिलाड़ियों के दो गुने) हॉकी खेलने वाले विद्यार्थियों की संख्या दर्शाएगा।
(ii) व्यंजक \(\frac { n }{ 2 }\) (फुटबॉल खिलाड़ियों के आधे) टेनिस खेलने वाले विद्यार्थियों की संख्या दर्शाएगा।
पाठ्य-पुस्तक पृष्ठ संख्या # 258
प्रश्न 1.
समीकरण के कुछ उदाहरण नीचे दिए जा रहे हैं। (कुछ समीकरणों में सम्बद्ध चर भी दिए गए हैं।)
वांछित रिक्त स्थानों को भरिए :
हल :
- x + 10 = 30 (चर x)
- p – 3 = 7 (चर p)
- 3n = 21 (चर n)
- \(\frac { t }{ 5 }\) = 4 (चर t)
- 2l + 3 = 7 (चर l)
- 2m – 3 = 5 (चर m)
![]()
पाठ्य-पुस्तक पृष्ठ संख्या # 259
प्रश्न 1.
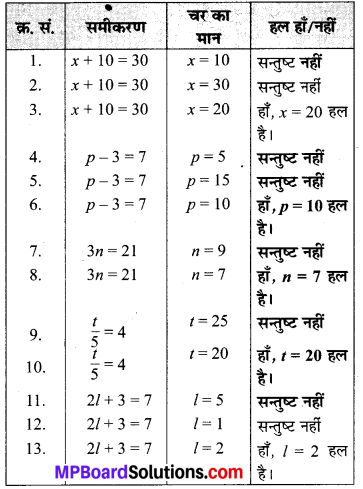
अब निम्नलिखित सारणी की प्रविष्टियों को पूरा कीजिए और स्पष्ट कीजिए कि आपके उत्तर हाँ/नहीं क्यों हैं ?
हल :