Category: Class 8

MP Board Class 8th Maths Solutions Chapter 10 Visualizing Solid Shapes Ex 10.2

Question 1.
Look at the given map of a city.

(a) Colour the map as follows : Blue-water, Red-fire station, Orange-library, Yellow- schools, Green-park, Pink-College, Purple- Hospital, Brown-Cemetery.
(b) Mark a green ‘X’ at the intersection of Road ‘C and Nehru Road, Green ‘Y’ at the intersection of Gandhi Road and Road A.
(c) In red, draw a short street route from Library to the bus depot.
(d) Which is further east, the city park or the market?
(e) Which is further south, the primary school or the Sr. Secondary School?
Solution:
(a), (b), (c)

Note : Students can colour the picture marked as respective colours,
(d) City park is further east.
(e) Sr. Secondary School is further south.

Question 2.
Draw a map of your class room using proper scale and symbols for different objects.
Solution:
Left for the students.

Question 3.
Draw a map of your school compound using proper scale and symbols for various features like playground, main building, garden etc.
Solution:
Left for the students.

Question 4.
Draw a map giving instructions to your friend so that she reaches your house without any difficulty.
Solution:
Left for the students.

MP Board Class 8th Maths Solutions

MP Board Class 8th Maths Solutions Chapter 10 Visualizing Solid Shapes Ex 10.1

Question 1.
For each of the given solid, the two views are given. Match for each solid the corresponding top and front views. The first one is done for you.

Solution:

Question 2.
For each of the given solid, the three views are given. Identify for each solid the corresponding top, front and side views.

Solution:

Question 3.
For each given solid, identify the top view, front view and side view.


Solution:

Question 4.
Draw the front view, side view and top view of the given objects.


Solution:

MP Board Class 8th Maths Solutions

MP Board Class 8th Maths Solutions Chapter 9 Algebraic Expressions and Identities Ex 9.5

Question 1.
Use a suitable identity to get each of the following products.
(i) (x + 3)(x + 3)
(ii) (2y + 5)(2y + 5)
(iii) (2a – 7)(2a – 7)

(v) (1.1m – 0.4)(1.1m + 0.4)
(vi) (a² + b²)(-a² + b²)
(vii) (6x – 7)(6x + 7)
(viii) (-a + c)(-a + c)

(x) (7a – 9b)(7a – 9b)
Solution:
(i) (x + 3) (x + 3) = (x + 3)2
= (x)² + 2(x)(3) + (3)²
[Using identity : (a + b)² = a² + 2ab + b²] = x² + 6x + 9

(ii) (2y + 5) (2y + 5) = (2y + 5)²
= (2y)² + 2(2y)(5) + (5)²
[Using identity : (a + b)² = a² + 2ab + b²] = 4a² + 20y + 25

(iii) (2a – 7)(2a – 7) = (2a – 7)²
= (2a)² – 2(2a)(7) + (7)²
[Using identity : (a – b)² = a² – 2ab + b²] = 4a² – 28a + 49

(v) (1.1m – 0.4) (1.1m + 0.4) = (1.1m)² – (0.4)²
[Using identity : a² – b² = (a + b) (a – b)]
= 1.21m² – 0.16

(vi) (a² + b²) (- a² + b²) = (b² + a²) (b² – a²)
= (b²)² – (a²)²
[Using identity : (a² – b²) = (a + b) (a – b)] = b⁴ – a⁴

(vii) (6x – 7) (6x + 7) = (6x)² – (7)² = 36x² – 49
[Using identity : (a² – b²) = (a + b) (a – b)]

(viii) (- a + c) (- a + c) = (c – a) (c – a) = (c – a)² = (c)² – 2(c)(a) + a²
[Using identity : (a – b)² = a² – 2ab + b²]
= c² – 2ac + a²

(x) (7a – 9b)(7a – 9b) = (7a – 9b)² = (7a)² – 2(7a)(9b) + (9b)²
[Using identity : (a – b)² = a²– 2ab + b²]
= 49a² – 126ab + 81b²

Question 2.
Use the identity
(x + a) (x + b) = x² + (a + b)x + ab to find the following products.
(i) (x + 3)(x + 7)
(ii) (4x + 5)(4x + 1)
(iii) (4x – 5)(4x – 1)
(iv) (4x + 5)(4x – 1)
(v) (2x + 5y)(2x + 3y)
(vi) (2a² + 9)(2a² + 5)
(vii) (xyz – 4)(xyz – 2)
Solution:
(i)(x + 3)(x + 7) = x² + (3 + 7)x + 3 × 7
= x² + 10x + 21

(ii) (4x + 5)(4x + 1) = (4x)² + (5 + 1)4x + 5 × 1
= 16x² + 24x + 5

(iii) (4x – 5) (4x – 1) – [4x + (-5)] [4x +(-1)]
= (4x)² + (-5 – 1)(4x) + (-5) × (-1)
= 16x² – 24x +5

(iv) (4x + 5) (4x – 1) (4x + 5) (4x + (-1)]
= (4x + (5 – 1)(4x) + (5) × (-1)
= 16x² + 16x – 5

(v) (2x + 5y)(2x + 3y)
= (2x)² + (5 + 3)y (2x) + (5y) × (3y)
= 4x² + 16xy + 15y²

(vi) (2a² + 9) (2a² + 5)
= (2a²)² + (9 + 5) (2a²) + 9 × 5
= 4a⁴ + 28a² +45

(vii) (xyz – 4) (xyz – 2)
= [xyz + (-4)] [xyz + (-2)]
= (xyz)² + (- 4 – 2) (xyz) + (- 4)(-2)
= x²y²z² – 6xyz + 8

Question 3.
Find the following squares by using the identities.
(i) (b – 7)²
(ii) (xy + 3z)²
(iii) (6x² – 5y)²

(v) (0.4p – 0.5q)²
(vi) (2xy + 5y)²
Solution:
(i) (b – 7)² = (b)² – 2(b)(7) + (7)²
[Using identity : (a – b)² = a² – 2ab + b²]
= b² – 14b + 49

(ii) (xy + 3z)² = (xy)² + (3z)² + 2(xy) (3z)
[Using identity : (a + b)² = a² + b² + 2ab]
= x²y² + 9z² + 6xyz

(iii) (6x² – 5y)² = (6x²)² + (5y)² – 2(6x²) (5y)
[Using identity : (a – b)² = a² + b² – 2ab]
= 36x⁴ + 25y² – 60x²y

(v) (0.4p – 0.5p)²
= (0.4p)² + (0.5q)² – 2(0.4p) (0.5q)
[Using identity : (a – b)² = a² + b² – 2ab]
= 0.16p² + 0.25q² – 0.4pq

(vi) (2xy + 5y)²
= (2xy)² + (5y)² + 2(2xy) (5y)
[Using identity : (a + b)² = a² + b² + 2ab] = 4x²y² + 25 y² + 20xy²

Question 4.
Simplify.
(i) (a² – b²)²
(ii) (2x + 5)² – (2x – 5)²
(iii) (7m – 8n)² + (7m + 8n)²
(iv) (4m + 5n)² + (5m + 4n)²
(v) (2.5p – 1.5q)² – (1.5p – 2.5q)²
(vi) (ab + bc)² – 2ab²c
(vii) (m² – n²m)² + 2m³n²
Solution:
(i) (a² – b²)² = (a²)² – 2a²b² + (b²)²
[Using identity : (a – b)² = a² – 2ab + b²]
= a⁴ – 2a²b² + b⁴

(ii) (2x + 5)² – (2x – 5)²
=[2x + 5 – (2x – 5)][2x + 5 + 2x – 5]
[Using identity : a² – b² – (a – b) (a + h)]
= (10)(4x) = 40x

(iii) (7m – 8n)² + (7m + 8n)²
= (7m)² – 2(7m) (8n) + (8n)² + (7m)² + 2(7m)(8n) + (8n)²
[Using identity : (a – b)² = a² – 2ab + b²]
and (a + b)² = a² + 2ab + b²]
= 49m² – 112mn + 64n² + 49m² + 112mn + 64n²
= 98m² + 128n²

(iv) (4m + 5n)² + (5m + 4n)²
(4m)² + 2(4m) (5n) + (5n)² + (5m)² + 2(5m)(4n) + (4n)²
(Using identity : (a + b)² = a² + 2ab + b²)
= 16m² + 40mn + 25n² + 25m² + 40mn + 16n²
= 41m² + 80mn + 41n²

(v) (2.5p – 1.5q)² – (1.5p – 2.5q)²
= (2.5p)² – 2(2.5p)(1.5q) + (1.5q)² – [(1.5p)² – 2(1.5p) (2.5q) + (2.5q)²]
[Using identity: (a – b)² = a² – 2ab + b²]
= 6.25p² – 7.5pq + 2.25q² – [225p² – 7.5pq + 6.25q²]
= 6.25p² – 7.5pq + 2.25q² – 2.25p² + 7.5pq – 6.25q²
= 4p² – 4q²

(vi) (ab + bc)² – 2ab²c
= (ab)² + 2(ab)(bc) + (bc)² – 2ab²c
[Using identity : (a + b)² = a² + 2ab + b²]
= a²b² + b²c² – 2ab²c + 2ab²c = a²b² + b²c²

(vii) (m² – n²n)² + 2m³n²
=(m²)² – 2(m²)(n²m) + (n²m)² + 2m³n²
[Using identity : (a – b)² = a² – 2ab + b²]
= m⁴ – 2m³n² + 2m³n² = m⁴ + n⁴m²

Question 5.
Show that
(i) (3x + 7)² – 84x = (3x – 7)²
(ii) (9p – 5q)² + 180pq = (9p + 5q)²

(iv) (4pq + 3q)² – (4pq – 3q)² = 48pq²
(v) (a – b)(a + b) + (b – c)(b + c) + (c – a)(c + a) = O
Solution:
(i) To prove: (3x + 7)² – 84x = (3x – 7)²
LH.S. = (3x + 7)² – 84x
= (3x)² + 2(3x)(7) + (7)² – 84x
= 9x² + 42x +49 – 84x = 9x² – 42x + 49
R.H.S. = (3x – 7)² = (3x)² – 2(3x)(7) + (7)² = 9x² – 42x + 49
∴ L.H.S. = R.H.S.

(ii) To prove : (9p – 5q)² + 180pq = (9p + 5q)²
L.H.S. = (9p – 5q)² + 180pq
= (9p)² – 2(9p)(5q) + (5q)² + 180pq
= 81p² – 90pq + 25q² + 180pq
= 81 p² + 90 pq + 25 q²
R.H.S. = (9p + 5q)²
= (9p)² + 2(9p)(5q) + (5q)²
= 81p² + 90pq + 25q²
∴ L.H.S. = R.H.S.

(iii) To prove :

(iv) To prove : (4pq + 3q)² – (4pq – 3q)² = 48pq²
L.H.S. = (4pq + 3q)² – (4pq – 3q)²
= (4 pq)² + 2(4pq)(3q) + (3q)² – [(4pq)² – 2(4pq)(3q) + (3q)²]
= 16p²q² + 24pq² + 9q² – [16p²q² – 24pq² + 9q²]
= 16p²q² + 24pq² + 9q²
= 16p²q² + 24pq² – 9q²
= 48pq² = R.H.S.

(v) To prove : (a – b) (a + b) + (b – c) (b + c) + (c – a) (c + a) = 0
L.H.S. = (a – b) (a + b) + (b – c) (b + c) + (c – a)(c + a)
= a² – b² + b² – c² + c² – a²
[Using identity : (x – y)(x + y) = x² – y²]
= 0 = R.H.S.

Question 6.
Using identities, evaluate,
(i) 71²
(ii) 99²
(iii) 102²
(iv) 998²
(v) 5.2²
(vi) 297 × 303
(vii) 78 × 82
(viii) 8.9²
(ix) 1.05 × 9.5
Solution:
(i) 71² = (70 + 1)²
= (70)² + 2(70)(1) + 1²
[Using identity : (a + b)² = a² + 2ab + b²]
= 4900 + 140 + 1 = 5041

(ii) 99² = (100 – 1)²
= (100)² – 2(100) (1) + 1²
[Using identity : (a – b)² = a² – 2ab + b²]
= 10000 – 200 + 1 = 9801

(iii) (102)² = (100 + 2)²
= (100)² + 2(100)(2) + 2²
[Using identity : (a + b)² = a² + 2ab + b²]
= 10000 + 400 + 4 = 10404

(iv) (998)² = (1000 – 2)²
= (1000)² – 2(1000)(2) + (2)²
[Using identity : (a – b)² = a² – 2ab + b²]
= 1000000 – 4000 + 4 = 996004

(v) (5.2)² = (5 + 0.2)²
= (5)² + 2(5)(0.2) + (0.2)²
[Using identity : (a + b)² = a² + 2ab + b²]
= 15 + 1 + 0.04 = 27.04

(vi) 297 ² × 303 = (300 – 3) (300 + 3)
= (300)² – 3²
[Using identity : (a – b) (a + b) = (a² – b²)
= 90000 – 9 = 89991

(vii) 78 × 82 = (80 – 2) (80 + 2)
= (80)² – (2)²
[Using identity : (a -b) (a + b) = a² – b²]
= 6400 – 4 = 6396

(viii) (8.9)² = (9 – 0.1)²
= (9)² – 2(9)(0.1) + (0.1)²
[Using identity : (a – b)² = a² – 2ab + b²] = 81 – 1.8 + 0.01 = 79.21

(ix) 1.05 × 9.5

Question 7.
Using a² – b² = (a + b)(a – b), find
(i) 51² – 49²
(ii) (1.02)² – (0.98)²
(iii) 153² – 147²
(iv) 12.1² – 7.9²
Solution:
(i) 51² – 49² = (51 – 49) (51 + 49)
= (2)(100) = 200
(ii) (1.02)² – (0.98)² = (1.02 – 0.98) (1.02 + 0.98)
= (0.04)(2) = 0.08
(iii) 153² – 147² = (153 + 147) (153 – 147)
= (300) (6) = 1800
(iv) (12.1)² – (7.9)² = (12.1 + 7.9) (12.1 – 7.9)
= (20.0) (4.2) = 84

Question 8.
Using (x + a)(x + b) = x² + (a + b)x + ab, find
(i) 103 × 104
(ii) 5.1 × 5.2
(iii) 103 × 98
(iv) 9.7 × 9.8
Solution:
(i) 103 × 104 = (100 + 3)(100 + 4)
= (100)² + (3 + 4) 100 + 3 × 4
= 10000 + 700 + 12 = 10712

(ii) 5.1 × 5.2 = (5 + 0.1)(5 + 0.2)
= (5)² +(0.1+ 0.2) × 5 + (0.1) (0.2)
= 25 + 1.5 + 0.02 = 26.52

(iii) 103 × 98 = (100 + 3) (100 – 2)
= (100 + 3) [100+ (- 2)]
= (100)² + (3 – 2) × 100 + (3) (- 2) = 10000 + 100 – 6 = 10094

(iv) 9.7 × 9.8 = (10 – 0.3) (10 – 0.2)
= [10 + (- 0.3)[10 + (- 0.2)]
= (10)² + (- 0 3 – 0 2) × 10 + (- 0.3) (- 0.2)
= 100 – 5 + 0.06 = 95.06

MP Board Class 8th Maths Solutions

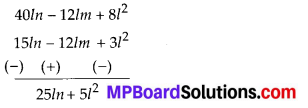
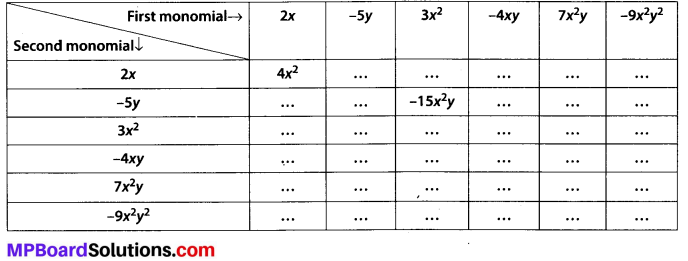
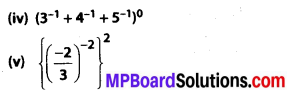
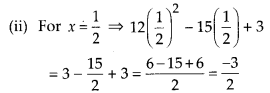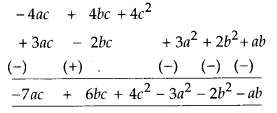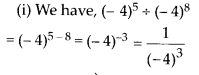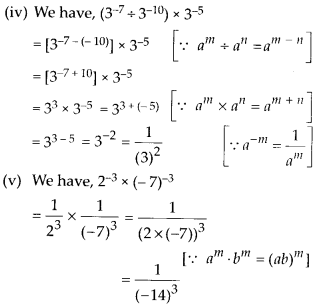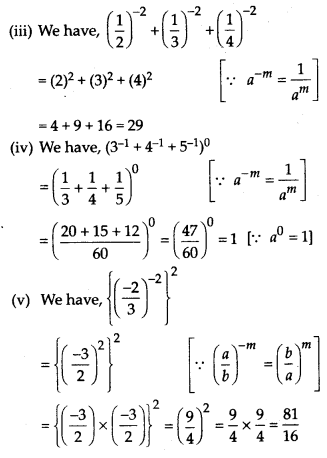MP Board Class 8th Maths Solutions Chapter 16 संख्याओं के साथ खेलना Ex 16.1

प्रश्न 1.
निम्नलिखित में से प्रत्येक में अक्षरों के मान ज्ञात कीजिए तथा सम्बद्ध चरणों के लिए कारण भी दीजिए –

हल:
1. इकाई स्तम्भ को जोड़ने पर अर्थात् A + 5 को जोड़ने पर हम इकाई का अंक 2 प्राप्त करते हैं।
अत: A = 7, (∴ A + 5 = 7 + 5 = 12)
अब दहाई स्तम्भ को जोड़ने पर
1 + 3 + 2 = B या B = 6
अतः अब पहेली इस प्रकार होगी –

∴ A = 7, B = 6

2. इकाई स्तम्भ से, A + 8 = 3
अर्थात् इकाई का अंक = 3 होना चाहिए।
अतः A = 5, (∴ A + 8 = 5 + 8 = 13)
अब दहाई स्तम्भ से, 1 + 4 + 9 = B या B = 14
∴ स्पष्ट है, B = 4 और C = 1 अब पहेली इस प्रकार होगी –

∴ A = 5, B = 4 तथा C = 1

3. क्योंकि इकाई का अंक A x A = A है।
∴ A = 1, A = 5 या A = 6
जबकि A = 1, तब,

अत: A ≠ 1
जबकि A = 5, तब,

अत: A ≠ 5
जबकि A = 6, तब,

अतः A = 6

4. दी हुई पहेली से,
B + 7 = A तथा A + 3 = 6
अतः सम्भावित मान
0 + 7 = 7 अर्थात् A = 7 परन्तु 7 + 3 ≠ 6
1 + 7 = 8 अर्थात् A = 8 परन्तु 8 + 3 ≠ 6
2 + 7 = 9 अर्थात् A = 9 परन्तु 9 + 3 ≠ 6
3 + 7 = 10 अर्थात् A = 0 परन्तु 1 + 0 + 3 ≠ 6
4 + 7 = 11 अर्थात् A = 1 परन्तु 1 + 1 + 3 ≠ 6
5 + 7 = 12 अर्थात् A = 2 और 1 + 2 + 3 = 6
B = 5 तथा A = 2
अब पहेली इस प्रकार है –

A = 2 और B = 5

5. ∴ इकाई स्तम्भ 3 x B = B, ∴ B = 0
अब पहेली इस प्रकार है –

अब, 3 x A = A, ∴ A = 5
अब, पहेली इस प्रकार है –

∴ A = 5, B = 0 और C = 16
6. ∴ इकाई स्तम्भ 5 x B = B अर्थात् B = 0 या 5
यदि B = 0, तब

अब, 5 x A = A या A = 0 या 5
परन्तु A0, A = 5 के लिए

∴ A = 5, B = 0 और C = 2
यदि B = 5, तब

अब, 5 x A + 2 = A ⇒ A = 2, ∴ 5 x 2 + 2 = 12
∴ इकाई का अंक = 2 = A
∴ B = 5 के लिए,

∴ A = 2, B = 5 और C = 1

7.

BBB के सम्भव मान: 111, 222, 333, आदि
∴ 111 ÷ 6 = 18 और शेषफल = 3 ∴ B ≠ 3
222 ÷ 6 = 37, शेषफल = 0, अतः भागफल 37 ≠ A2
333 ÷ 6 = 55, शेषफल = 3, अतः भागफल 55 ≠ A3
444 + 6 = 74, शेषफल = 4, अतः भागफल 74 ≠ A4
अतः A = 7 और B = 4

8. इकाई स्तम्भ से 1 + B = 0, इकाई स्तम्भ का अंक 0 है।
∴ B = 9 अब

परन्तु 90 – 19 = 71 अत: A1 = 71 या A = 7
अतः A = 7, B = 9

9. इकाई स्तम्भ से,
B + 1 = 8 अतः इकाई अंक 8 है।
B = 8 – 1 = 7
∴ B स्वयं एक अंक है, ∴ B = 7
अब

दहाई स्तम्भ से, A + 7 = 1
अतः A का इकाई अंक 1 होना चाहिए।
∴ A स्वयं एक अंक है। अत: A = 4
अब, पहेली

अतः A = 4, B = 7

10. दहाई के स्तम्भ से,
2 + A = 0
∴ संख्या का इकाई अंक 0 होना चाहिए।
∴ A = 8, तब

अब, 8 + B = 9, ∴ B = 9 – 8 = 1
अब,

∴ A = 8 और B = 1

पाठ्य-पुस्तक पृष्ठ संख्या # 268

प्रयास कीजिए (क्रमांक 16.6)

(पहला प्रश्न आपकी सहायता के लिए किया हुआ है।)
प्रश्न 1.
यदि विभाजन N ÷ 5 से शेषफल, 3 प्राप्त होता है, तो N की इकाई अंक क्या हो सकता है?
हल:
इकाई के अंक को 5 से भाग देने पर शेषफल 3 आना चाहिए। अतः इकाई का अंक 3 या 8 होगा।

प्रश्न 2.
यदि विभाजन N ÷ 5 से शेषफल 1 प्राप्त होता है, तो N का इकाई अंक क्या हो सकता है?
हल:
इकाई के अंक को 5 से भाग देने पर शेषफल 1 आना चाहिए।
अतः इकाई का अंक 1 या 6 होगा।

प्रश्न 3.
यदि विभाजन N 5 से शेषफल 4 प्राप्त होता है, तो N की इकाई का अंक क्या हो सकता है?
हल:
इकाई के अंक को 5 से भाग देने पर शेषफल 4 आना चाहिए।
अतः इकाई का अंक 4 या 9 होगा।

प्रयास कीजिए (क्रमांक 16.7)

(पहला प्रश्न आपकी सहायता के लिए किया हुआ है।)
प्रश्न 1.
यदि विभाजन N ÷ 2 से शेषफल 1 प्राप्त होता है, तो N की इकाई का अंक क्या हो सकता है?
हल:
N विषम है। इसलिए इसकी इकाई का अंक विषम होगा। अतः N की इकाई का अंक 1, 3, 5, 7 या 9 होगा।

प्रश्न 2.
यदि विभाजन N ÷ 2 से कोई शेष प्राप्त नहीं होता (अर्थात् शेषफल 0 है), तो N की इकाई का अंक क्या हो सकता है?
हल:
N सम होना चाहिए। इसलिए इसकी इकाई का अंक सम होगा। – अंत: N की इकाई का अंक 0, 2, 4, 6 या 8 होगा।

प्रश्न 3.
मान लीजिए कि विभाजन N ÷ 5 से शेषफल 4 और विभाजन N ÷ 2 से 1 प्राप्त होता है। N की इकाई का अंक क्या होना चाहिए?
हल:
क्योंकि N ÷ 5 से शेषफल 4 प्राप्त होता है। अत: N की इकाई का अंक 4 या 9 होगा।
N ÷ 2 से शेषफल 1 प्राप्त होता है। इसलिए इकाई का अंक विषम होना चाहिए।
अतः N की इकाई का अंक 1, 3, 5, 7 या 9 होगा। परन्तु यहाँ 9 दोनों स्थितियों को सन्तुष्ट करेगा।
अतः N की इकाई का अंक 9 होगा।

पाठ्य-पुस्तक पृष्ठ संख्या # 270

प्रयास कीजिए (क्रमांक 16.8)

प्रश्न 1.
निम्नलिखित संख्याओं की 9 से विभाज्यता की जाँच कीजिए –

1. 108
2. 616
3. 294
4. 432
5. 927

हल:
हम जानते हैं कि कोई संख्या 9 से विभाज्य होती है, यदि इसके अंकों का योग 9 से विभाज्य हो।

1. संख्या = 108
संख्या के अंकों का योग = 1 + 0 + 8 = 9, यह 9 से विभाज्य है।
इसलिए 108, 9 से विभाज्य है।

2. संख्या = 616
संख्या के अंकों का योग = 6 + 1 + 6 = 13, यह 9 से विभाज्य नहीं है।
इसलिए 616, 9 से विभाज्य नहीं है।

3. संख्या = 294
संख्या के अंकों का योग = 2 + 9 + 4 = 15, यह 9 से विभाज्य नहीं है।
इसलिए 294, 9 से विभाज्य नहीं है।

4. संख्या = 432
संख्या के अंकों का योग = 4 + 3 + 2 = 9, यह 9 से विभाज्य है।
इसलिए 432, 9 से विभाज्य है।

5. संख्या = 927
संख्या के अंकों का योग = 9 + 2 + 7 = 18, यह 9 से विभाज्य है।
इसलिए 927, 9 से विभाज्य है।

सोचिए, चचों कोजिए और लिखिए।

प्रश्न 1.
आप देख चुके हैं कि 450, 10 से विभाज्य है। यह 2 और 5 से भी विभाज्य है, जो 10 के गुणनखण्ड हैं। इसी प्रकार संख्या 135, 9 से विभाज्य है। यह 3 से भी विभाज्य है, जो 9 का एक गुणनखण्ड है।
क्या आप कह सकते हैं कि यदि कोई संख्या किसी संख्या m से विभाज्य हो, तो वह m के प्रत्येक गुणनखण्ड से भी विभाज्य होगी?
हल:
हाँ, यदि कोई संख्या m से विभाज्य हो, तो वह m के प्रत्येक गुणनखण्ड से भी विभाज्य होगी।

प्रश्न 2.
1. एक तीन अंकों की संख्या abc की 100 a + 10b + c के रूप में लिखिए। अब 100a + 10b + c = 99a + 11b + (a – b + c)
= 11 (9a + b) + (a – b + c)
यदि संख्या abc, 11 से विभाज्य है, तो आप (a-b+ c) के बारे में क्या कह सकते हैं ? क्या यह आवश्यक है कि (a+c-b), 11 से विभाज्य हो?

2. एक चार अंकों की संख्या abcd को इस प्रकार लिखिए –
1000a + 100b + 10c + d = (1001 a + 99b + 11c) -(a – b + c – d)
= 11 (91a + 9b + c) + [(b + d) – (a + c)]
यदि संख्या abcd, 11 से विभाज्य है, तो (b + d) – (a + c) के बारे में आप क्या कह सकते हैं?

3. उपर्युक्त (i) और (ii) से, क्या आप कह सकते हैं कि कोई संख्या 11 से विभाज्य होगी, यदि इसके विषम स्थानों के अंकों का योग और समस्थानों के अंकों के योग का अन्तर 11 से विभाज्य होगा?

हल:
1. हाँ, यह आवश्यक है कि (a + c – d), 11 से विभाज्य होगी।
2. यदि संख्या abcd, 11 से विभाज्य है, तब (b + d) – (a + c), 11 से विभाज्य होगी।
3. हाँ, हम कह सकते हैं कि यदि कोई संख्या 11 से विभाज्य होगी यदि इसके विषम स्थानों के अंकों का योग और समस्थानों के अंकों का योग का अन्तर 11 से विभाज्य हो।

पाठ्य-पुस्तक पृष्ठ संख्या # 271

प्रयास कीजिए (क्रमांक 16.9)

प्रश्न 1.
निम्नलिखित संख्याओं की 3 से विभाज्यता की जाँच कीजिए –

1. 108
2. 616
3. 294
4. 432
5. 927.

हल:
हम जानते हैं कि कोई संख्या 3 से विभाज्य होती है, यदि इसके अंकों का योग 3 से विभाज्य हो।
1. संख्या = 108
अंकों का योग = 1 + 0 + 8 = 9, यह 3 से विभाज्य है।
इसलिए 108,3 से विभाज्य है।

2. संख्या = 616
अंकों का योग = 6 + 1 + 6 = 13, यह 3 से विभाज्य नहीं है।
इसलिए 616, 3 से विभाज्य नहीं है।

3. संख्या = 294
अंकों का योग = 2 + 9 + 4 = 15, यह 3 से विभाज्य है।
इसलिए 294, 3 से विभाज्य है।

4. संख्या = 432
अंकों का योग = 4 + 3 + 2 = 9, यह 3 से विभाज्य है।
इसलिए 432, 3 से विभाज्य है।

5. संख्या = 927
अंकों का योग = 9 + 2 + 7 = 18, यह 3 से विभाज्य है।
इसलिए 927, 3 से विभाज्य है।

MP Board Class 8th Maths Solutions

MP Board Class 8th Maths Solutions Chapter 9 Algebraic Expressions and Identities Ex 9.4

Question 1.
Multiply the binomials.
(i) (2x + 5) and (4x – 3)
(ii) (y – 8) and (3y – 4)
(iii) (2.5l – 0.5 m) and (2.5l +0.5 m)
(iv) (a + 3b) and (x + 5)
(v) (2pq + 3q²) and (3pq – 2q²)

Solution:
(i) (2x + 5) × (4x – 3) = 2x (4x – 3) + 5(4x – 3) = 8x² – 6x + 20x – 15 = 8x² + 14x – 15
(ii) (y – 8) × (3y – 4) = y(3y – 4) – 8(3y – 4)
= 3 y² – 4y – 24y + 32 = 3y² – 28y + 32
(iii) (2.5l – 0.5m) × (2.5l + 0.5m)
= 2.5l (2.5l + 0.5m) – 0.5 m (2.5l + 0.5m)
= 6.25l² + 1.25lm – 1.25lm – 0.25m² = 6.25l² – 0.25m²
(iv) (a + 3b) × (x + 5) = a(x + 5) + 3b(x + 5)
= ax + 5a + 3 bx + 15 b
(v) (2pq + 3q²) × (3pq – 2q²)
= 2pq (3pq – 2q²) + 3q² (3pq – 2q²)
= 6p²q² – 4pq³ + 9pq³ – 6q⁴
= 6 p²q² + 5pq³ – 6q⁴

Question 2.
Find the product
(i) (5 – 2x)(3 + x)
(ii) (x + 7y)(7x – y)
(iii) (a² + b)(a + b²)
(iv) (p² – q²)(2p + q)
Solution:
(i) (5 – 2x) × (3 + x) = 5(3 + x) – 2x(3 + x)
= 15 + 5x – 6x – 2x² – 15 – x – 2x²
(ii) (x + 7y)(7x – y) = x(7x – y) + 7y(7x – y)
=7x² – xy + 49xy – 7y² = 7x² + 48xy – 7y²
(iii) (a² + b) (a + b²) = a² (a + b²) + b (a + b²)
= a³ + a²b²) + ab + b³
(iv) (p² – q²) (2p + q) = p² (2p + q) – q² (2p + q)
= 2p³ + p²q – 2q²p – q³

Question 3.
Simplify.
(i) (x² – 5)(x + 5) + 25
(ii) (a² + 5)(b³ + 3) + 5
(iii) (t + s²)(t² – s)
(iv) (a + b)(c – d) + (a – b)(c + d) + 2(ac + bd)
(v) (x + y)(2x + y) + (x + 2y)(x – y)
(vi) (x + y)(x² – xy + y²)
(vii) (1 .5x – 4y)(1 .5x + 4y + 3) – 4.5x + 12y
(viii) (a + b + c)(a + b – c)
Solution:
(i) (x² – 5) (x + 5) + 25
= x²(x +5) – 5(x + 5) +25
=x³+ 5x² – 5x – 25 + 25 = r³+ 5r² – 5x

(ii) (a² + 5)(b³ + 3) + 5
= a² (b³ + 3) + 5(b³ + 3) + 5
= a²b³ + 3a² + 5b³ + 15 + 5
= a²b³ + 3a² + 5b³ + 20

(iii) (t + s²) (t² – s) = t(t² – s) + s²(t² – s)
= t³ – ts +s²t² – s³

(iv) (a + b)(c – d) + (a – b)(c + d) + 2(ac + bd)
=a(c – d) + b(c – d) + a(c + d) – b(c + d) + 2a + 2bd
= ac – ad + bc – bd + ac + ad – bc – bd + 2ac + 2bd
= 4ac

(v) (x + y)(2x + y) + (x + 2y)(x – y)
= x(2x + y) + y(2x + y) + x(x – y) + 2y(x – y)
=2x² + xy + 2xy + y² + x² – xy + 2xy – 2y²
= 3x² + 4xy – y²

(vi) (x + y) (x² – xy + y²)
= x (x² – xy + y²) + y (x² – xy + y²)
= x³ – x²y + xy² + x²y – xy² + y³ = x³ + y³

(vii) (1.5x – 4y) (1.5x + 4y + 3) – 4.5x + 12y
= 1.5x (1.5x + 4y + 3) – 4y (1.5x + 4y + 3) – 4.5x + 12y
= 2.25x² + 6xy + 4.5x – 6xy – 16y² – 12y – 4.5x + 12y
= 2.25x² – 16y²

(viii) (a + b + c) (a + b – c)
= a (a+ b – c) + b (a+ b – c) + c (a + b – c)
= a² + ab – ac + ab + b² – bc + ac + bc – c²
= a² + 2 ab + b² – c²

MP Board Class 8th Maths Solutions

MP Board Class 8th Maths Solutions Chapter 9 Algebraic Expressions and Identities Ex 9.3

Question 1.
Carry out the multiplication of the expressions in each of the following pairs.
(i) 4p, q + r
(ii) ab, a – b
(iii) a + b, 7a²b²
(iv) a² – 9, 4a
(v) pq + qr + rp, 0
Solution:
(i) 4p × (q + r) = 4p × q + 4p × y = 4pq + 4pr
(ii) ab × (a – b) = a²b – ab²
(iii) (a + b) × 7a²b² = 7a³b² + 7a²b³
(iv) (a² – 9) × (4a) = 4a³ – 36a
(v) (pq + qr + rp) × 0 = 0

Question 2.
Complete the table.

Solution:

Question 3.
Find the product.
(i) (a²) × (2a²²) × (4a²⁶)

(iv) x × x² × x³ × x⁴
Solution:

Question 4.
(a) Simplify 3x(4x – 5) + 3 and find its values for
(i) x = 3
(ii) x = \(\frac{1}{2}\)
(b) Simplify a(a² + a + 1) + 5 and find its value for
(i) o = 0
(ii) a = 1
(iii) a = – 1
Solution:
(a) 3x(4x – 5) + 3 = 12x² – 15x + 3
(i) For x = 3,
12(3)² – 15(3) + 3 = 108 – 45 + 3 = 66

(b) a(a² + a + 1) + 5 = a³ + a² + a + 5
(i) For a = 0, (0)³ + 0² + 0 + 5 = 5
(ii) For a = 1, 1³ + 1² + 1 + 5 = 8
(iii) For a = -1, (-1)³ + (-1)² + (-1) + 5 = -1 + 1 – 1 + 5 = 4

Question 5.
(a) Add: p(p – q), q(q – r) and r(r – p)
(b) Add : 2x(z – x – y) and 2y(z – y – x)
(c) Subtract: 3l(l -4m + 5n) from 4l(10n – 3m + 2l)
(d) Subtract: 3o(a + b + c) – 2b(a – b + c) from 4c(-a + b + c)
Solution:
(a) First expression
= p(p – q) = p² – pq
Second expression = q(q- r) = q² – qr… (ii)
Third expression = r(r – p) = r² – pr ….(iii)
Adding (i), (ii) and (iii), we get
p² – pq + q² – qr + r² – pr = p² + q² + r² – pq – qr – pr

(b) First expression = 2x(z -x-y)
= 2xz – 2x² – 2xy
Second expression = 2y(z -y-x)
= 2yz – 2y² – 2xy
Adding the two expressions, we get

(c) First expression = 3l(l – 4m + 5n)
= 3l² – 121m + 15In
Second expression = 4l(10n – 3m + 2l)
= 40ln – 12lm + 8l²
Subtracting the two expressions, we get 40/n –

(d)
First expression= 3a(a + b + c) – 2b(a – b + c)
= 3a²+3ab + 3ac – 2ab + 2b² – 2bc
= 3a² + ab + 2b² + 3ac – 2bc
Second expression = 4c(- a + b + c)
= – 4ac + 4bc + 4c²
Subtracting the two expressions, we get

MP Board Class 8th Maths Solutions

MP Board Class 8th Maths Solutions Chapter 9 Algebraic Expressions and Identities Ex 9.2

Question 1.
Find the product of the following pairs of monomials.
(i) 4, 7p
(ii) -4p, 7p
(iii) -4p, 7pq
(iv) 4p³, -3p
(v) 4p, 0
Solution:
(i) 4 × 7p = 28p
(ii) -4p × 7p = -28p
(iii) -4p × 7pq = -28p
(iv) 4p³ × -3p = -12p⁴
(v) 4p × 0 = 0

Question 2.
Find the areas of rectangles with the following pairs of monomials as their lengths and breadths respectively.
(p, q); d (10m, 5n); (20x², 5y²); (4x, 3x²); (3mn, 4np)
Solution:

Question 3.
Complete the table of products.

Solution:

Question 4.
Obtain the volume of rectangular boxes with the following length, breadth and height respectively.
(i) 5a, 3a², 7a⁴
(ii) 2p, 4q, 8r
(iii) xy, 2x²y, 2xy²
(iv) a, 2b, 3c
Solution:

Question 5.
Obtain the product of
(i) xy, yz, zx
(ii) a, -a², a²
(iii) 2, 4y, 8y², 16y³
(iv) a, 2b, 3c. 6abc
(v) m, – mn, mnp
Solution:
(i) xy × yz × zx = x²y²z²
(ii) a × (-a²) × a³ = – a⁶
(iii) 2 × ⁴y × 8y² × 16y³ = 1024y⁶
(iv) a × 2b × 3c × 6abc = 36a²b²c²
(v) m × (- mn) × mnp = – m³n²p

MP Board Class 8th Maths Solutions

MP Board Class 8th Maths Solutions Chapter 9 Algebraic Expressions and Identities Ex 9.1

Question 1.
Identify the terms, their coefficients for each of the following expressions.
(i) 5xyz² – 3zy
(ii) 1 + x + x²
(iii) 4x²y² – 4x²y²z² + z2
(iv) 3 – pq + qr – rp
(v) \(\frac{x}{2}+\frac{y}{2}-x y\)
(vi) 0.3a – 0.6ab + 0.5b
Solution:

Question 2.
Classify the following polynomials as monomials, binomials, trinomials. Which polynomials do not fit in any of these three categories?
x + y, 1000, x + x² + x³ + x⁴, 7 + y + 5x, 2y – 3y², 2y – 3y² + 4y³, 5x – 4y + 3xy, 4z – 15z², ab + bc + cd + da, pqr, p²q, 9a², 2p + 2q
Solution:

Question 3.
Add the following:
(i) ab – bc, bc – ca, ca – ab
(ii) a – b + ab, b – c + bc, c – a + ac
(iii) 2p²q² – 3pq + 4, 5 + 7pq – 3p²q²
(iv) l² + m², m² + n², n² + l², 2lm + 2mn + 2nl
Solution:

Question 4.
(a) Subtract 4a – 7ab + 3b + 12 from 12a – 9ab + 5b – 3
(b) Subtract 3xy + 5yz – 7zx from 5xy – 2yz – 2zx + 10xyz
(c) Subtract 4p²q – 3pq + 5pq² – 8p + 7q – 10 from 18 – 3p – 11q + 5pq – 2pq² + 5p²q
Solution:

MP Board Class 8th Maths Solutions

MP Board Class 8th Maths Solutions Chapter 12 Exponents and Powers Ex 12.2

Question 1.
Express the following numbers in standard form.
(i) 0.0000000000085
(ii) 0.00000000000942
(iii) 6020000000000000
(iv) 0.00000000837
(v) 31860000000
Solution:
(i) 0.0000000000085 = 8.5 × 10^-12
(ii) 0.00000000000942 = 9.42 × 10^-12
(iii) 6020000000000000 = 6.02 × 10¹⁵
(iv) 0.00000000837 = 8.37 × 10^-9
(v) 31860000000 = 3.186 × 10¹⁰

Question 2.
Express the following numbers in usual form.
(i) 3.02 × 10^-6
(ii) 4.5 × 10⁴
(iii) 3 × 10^-8
(iv) 1.0001 × 10⁹
(v) 5.8 × 10¹²
(vi) 3.61492 × 10⁶
Solution:
(i) We have, 3.02 × 10^-6 = 0.00000302
(ii) We have, 4.5 × 10⁴ = 45000
(iii) We have, 3 × 10^-8 = 0.00000003
(iv) We have, 1.0001 × 10⁹ = 1000100000
(v) We have, 5.8 × 10¹² = 5800000000000
(vi) We have, 3.61492 × 10⁶ = 3614920

Question 3.
Express the number appearing in the following statements in standard form.
(i) 1 micron is equal to \(\frac{1}{1000000}\) m.
(ii) Charge of an electron is 0. 000,000,000,000,000,000,16 coulomb.
(iii) Size of a bacteria is 0.0000005 m.
(iv) Size of a plant cell is 0.00001275 m.
(v) Thickness of a thick paper is 0.07 mm.
Solution:
(i) Standard form of given statement = 1 × 10^-8.
(ii) Standard form of given statement = 1.6 × 10^-19.
(iii) Standard form of given statement = 5 × 10^-7.
(iv) Standard form of given statement = 1.275 × 10^-5.
(v) Standard form of given statement = 7 × 10^-2.

Question 4.
In a stack there are 5 books each of thickness 20 mm and 5 paper sheets each of thickness 0.016 mm. What is the total thickness of the stack.
Solution:
Total number of books = 5
Thickness of each book = 20 mm
∴ Thickness of 5 books = (5 × 20) mm = 100 mm
Thickness of each paper sheet = 0.016 mm
∴ Thickness of 5 paper sheets = (5 × 0.016) mm = 0.08 mm
Hence, total thickness of stack = 100 mm + 0.08 mm
= 100.08 mm = 1.0008 × 10² mm

MP Board Class 8th Maths Solutions

MP Board Class 8th Maths Solutions Chapter 12 Exponents and Powers Ex 12.1

Question 1.
Evaluate
(i) 3^-2
(ii) (-4)^-2
(iii) \(\)
Solution:

Question 2.
Simplify and express the result in power notation with positive exponent.

Solution:

Question 3.
Find the value of
(i) (3⁰ + 4^-1) × 2²
(ii) (2^-1 × 4^-1) ÷ 2^-2
(iii) \(\left(\frac{1}{2}\right)^{-2}+\left(\frac{1}{3}\right)^{-2}+\left(\frac{1}{4}\right)^{-2}\)

Solution:

Question 4.
Evaluate

Solution:

Question 5.
Find the value of m for which 5^m ÷ 5^-3 = 5⁵.
Solution:
We have, 5^m ÷ 5^-3 = 5⁵
⇒ 5^m-(-3) = 5⁵ [∵ a^m + aⁿ =a^{m + n}]
⇒ 5^{m + 3} = 5⁵
⇒ m + 3 = 5 [∵ a^m = aⁿ ⇒ m = n]
⇒ m = 5 – 3 = 2

Question 6.
Evaluate

Solution:

Question 7.
Simplify.

Solution:

MP Board Class 8th Maths Solutions