Category: Class 6

MP Board Class 6th Maths Solutions Chapter 13 Symmetry Ex 13.1

Question 1.
List any four symmetrical objects from your home or school.
Solution:
Notebook. Blackboard, Glass, Inkpot.

Question 2.
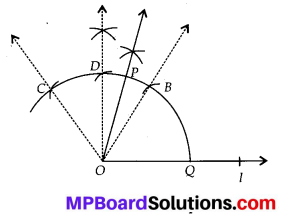
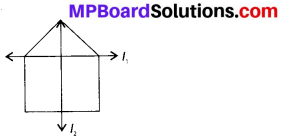
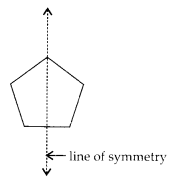
For the given figure, which one is the mirror line, l₁, or l₂?

Solution:
l₂ is the mirror line as both sides of the line are symmetric.

Question 3.
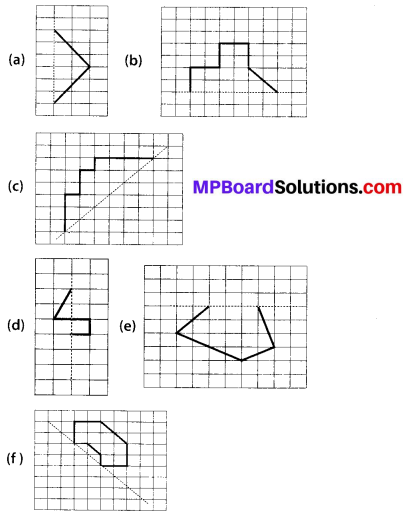
Identify the shapes given below. Check whether they are symmetric or not. Draw the line of symmetry as well.

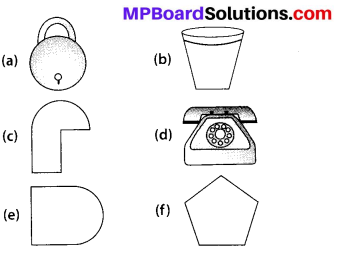
Solution:
(a) Symmetric

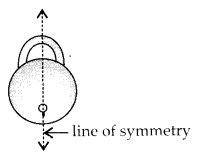
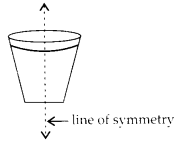
(b) Symmetric

(c) Not Symmetric
(d) Symmetric

(e) Symmetric

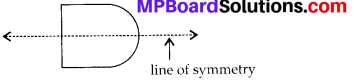
(f) Symmetric

Question 4.
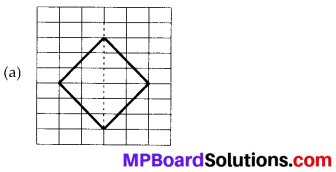
Copy the following on a squared paper. A square paper is what you would have used in your arithmetic notebook in earlier classes. Then complete them such that the dotted line is the line of symmetry.

Solution:

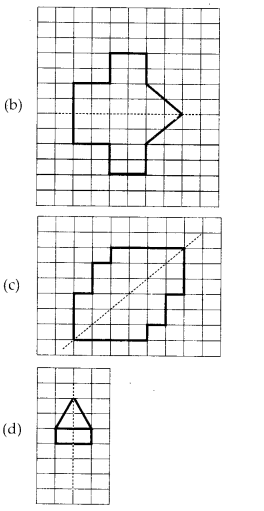
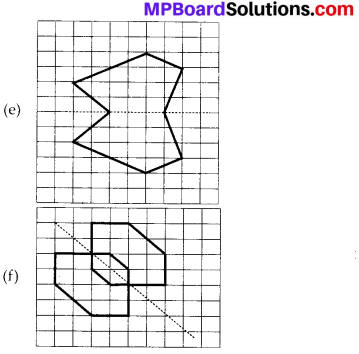
Question 5.
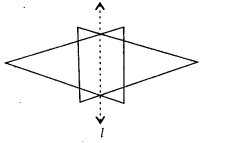
In thefigure, l is the line of symmetry. Complete the diagram to make it symmetric.

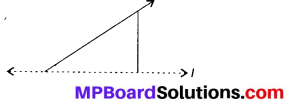
Solution:

Question 6.
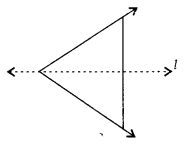
In the figure, l is the line of symmetry. Draw the image of the triangle and complete the diagram so that it becomes symmetric.

Solution:

MP Board Class 6th Maths Solutions

MP Board Class 6th Maths Solutions Chapter 3 Playing With Numbers Ex 3.5

Question 1.
Which of the following statements are true?
(a) If a number is divisible by 3, it must be divisible by 9.
(b) If a number is divisible by 9, it must be divisible by 3.
(c) A number is divisible by 18, if it is divisible by both 3 and 6.
(d) If a number is divisible by 9 and 10 both, then it must be divisible by 90.
(e) If two numbers are co-primes, at least one of them must be prime.
(f) All numbers which are divisible by 4 must also be divisible by 8.
(g) All numbers which are divisible by 8 must also be divisible by 4.
(h) If a number exactly divides two numbers separately, it must exactly divide their sum.
(i) If a number exactly divides the sum of two numbers, it must exactly divide the two numbers separately.
Solution:
Statements (b), (d), (g) and (h) are true.

Question 2.
Here are two different factor trees for 60. Write the missing numbers.

Solution:
Factors of 60 are 1, 2, 3, 4, 5, 6,10,12,15, 20, 30, 60.
(a) Since 6 = 2 × 3 and 10 = 5 × 2
∴ The missing numbers are 3 and 2.

(b) Since, 60 = 30 × 2, 30 = 10 × 3, and 10 = 5 × 2

Question 4.
Write the greatest 4-digit number and express it in terms of its prime factors.
Solution:
The greatest four digit number is 9999.

Question 5.
Write the smallest 5-digit number and express it in the form of its prime factors.
Solution:
The smallest five digit number is 10000.

Question 6.
Find all the prime factors of 1729 and arrange them in ascending order. Now state the relation, if any; between two consecutive prime factors.
Solution:

∴ 1729 = 7 × 13 × 19.
The difference of two consecutive prime factors is 6. (∵ 13 – 7 = 6 and 19 – 13 = 6)

Question 7.
The product of three consecutive numbers is always divisible by 6. Verify this statement with the help of some examples.
Solution:
Among the three consecutive numbers, there must be atleast one even number and one multiple of 3. Thus, the product must be divisible by 6.
For example :
(i) 2 × 3 × 4 = 24
(ii) 4 × 5 × 6 = 120,
where both 24 and 120 are divisible by 6.

Question 8.
The sum of two consecutive odd numbers is divisible by 4. Verify this statement with the help of some examples.
Solution:
The sum of two consecutive odd numbers is divisible by 4.
For example : 3 + 5 = 8 and 8 is divisible by 4.
5 + 7 = 12 and 12 is divisible by 4.
7 + 9 = 16 and 16 is divisible by 4.
9 + 11 = 20 and 20 is divisible by 4.

Question 9.
In which of the following expressions, prime factorisation has been done?
(a) 24 = 2 × 3 × 4
(b) 56 = 7 × 2 × 2 × 2
(c) 70 = 2 × 5 × 7
(d) 54 = 2 × 3 × 9
Solution:
In expressions (b) and (c), prime factorisation has been done.

Question 10.
Determine if 25110 is divisible by 45.
[Hint: 5 and 9 are co-prime numbers. Test the divisibility of the number by 5 and 9],
Solution:
The prime factorisation of 45 = 5 × 9
25110 is divisible by 5 as ‘0’ is at its unit place.
25110 is divisible by 9 as sum of digits (i.e., 9) is divisible by 9.
Therefore, the number 25110 must be divisible by 5 × 9 = 45

Question 11.
18 is divisible by both 2 and 3. It is also divisible by 2 × 3 = 6. Similarly, a number is divisible by both 4 and 6. Can we say that the number must also be divisible by 4 × 6 = 24? If not, give an example to justify your answer.
Solution:
No. The number 12 is divisible by both 6 and 4, but 12 is not divisible by 24.
∴ A number divisible by both 4 and ( may or may not be divisible by 4 × 6 = 24.

Question 12.
I am the smallest number, having four different prime factors. Can you find me?
Solution:
Since, 2 × 3 × 5 × 7 = 210
∴ 210 is the smallest number, having 4
different prime factors i.e., 2, 3, 5 and 7.

MP Board Class 6th Maths Solutions

MP Board Class 6th Maths Solutions Chapter 3 Playing With Numbers Ex 3.4

Question 1.
Find the common factors of:
(a) 20 and 28
(b) 15 and 25
(c) 35 and 50
(d) 56 and 120
Solution:
(a) Factors of 20 are 1, 2, 4, 5, 10 and 20
Factors of 28 are 1, 2, 4, 7,14 and 28
∴ Common factors of 20 and 28 are 1, 2 and 4

(b) Factors of 15 are 1, 3, 5 and 15
Factors of 25 are 1, 5 and 25
∴ Common factors of 15 and 25 are 1 and 5

(c) Factors of 35 are 1, 5, 7 and 35
Factors of 50 are 1, 2, 5, 10, 25 and 50
∴ Common factors of 35 and 50 are 1 and 5

(d) Factors of 56 are 1, 2, 4, 7, 8, 14, 28 and 56
Factors of 120 are 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60 and 120
∴ Common factors of 56 and 120 are 1, 2, 4 and 8

Question 2.
Find the common factors of:
(a) 4, 8 and 12
(b) 5,15 and 25
Solution:
(a) Factors of 4 are 1, 2 and 4 Factors of 8 are 1, 2, 4 and 8 Factors of 12 are 1, 2, 3, 4, 6 and 12
∴ Common factors of 4, 8 and 12 are 1, 2 and 4

(b) Factors of 5 are 1 and 5 Factors of 15 are 1, 3, 5 and 15
Factors of 25 are 1, 5 and 25 .-. Common factors of 5, 15 and 25 are 1 and 5

Question 3.
Find first three common multiples of:
(a) 6 and 8
(b) 12 and 18
Solution:
(a) Multiples of 6 are 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66, 72,
Multiples of 8 are 8, 16, 24, 32, 40, 48, 56, 64, 72,
∴ First three common multiples of 6 and 8 are 24, 48 and 72

(b) Multiples of 12 are 12, 24, 36, 48, 60, 72, 84, 96, 108, 120,
Multiples of 18 are 18, 36, 54, 72, 90, 108, 126,
∴ First three common multiples of 12 and 18 are 36, 72 and 108

Question 4.
Write ail the numbers less than 100 which are common multiples of 3 and 4.
Solution:
Multiples of 3 are 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42, 45, 48, 51, 54, 57, 60, 63, 66, 69, 72, 75, 78, 81, 84, 87, 90, 93, 96, 99,
Multiples of 4 are 4, 8, 12,16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56, 60, 64, 68, 72, 76, 80, 84, 88, 92, 96, 100
Common multiples of 3 and 4 which are less than 100 are 12, 24, 36, 48, 60, 72, 84 and 96

Question 5.
Which of the following numbers are co-prime?
(a) 18 and 35
(b) 15 and 37
(c) 30 and 415
(d) 17 and 68
(e) 216 and 215
(f) 81 and 16
Solution:
(a) Factors of 18 are 1, 2, 3, 6, 9 and 18
Factors of 35 are 1, 5, 7 and 35 Common factor of 18 and 35 is 1 Since, both have only one common factor, i.e., 1.
Therefore, 18 and 35 are co-prime numbers.

(b) Factors of 15 are 1, 3, 5 and 15
Factors of 37 are 1 and 37 Common factor of 15 and 37 is 1
Since, both have only one common factor, i.e., 1. Therefore, 15 and 37 are co-prime numbers.

(c) Factors of 30 are 1, 2, 3, 5, 6, 10, 15 and 30
Factors of 415 are 1, 5, , 83 and 415
Common factors of 30 and 415 are 1 and 5
Since, both have more than one common factor. Therefore, 30 and 415 are not co-prime numbers.

(d) Factors of 17 are 1 and 17
Factors of 68 are 1, 2, 4, 17, 34 and 68 Common factors of 17 and 68 are 1 and 17
Since, both have more than one common factor. Therefore, 17 and 68 are not co-prime numbers.

(e) Factors of 216 are 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 27, 36, 54, 72, 108 and 216
Factors of 215 are 1, 5, 43 and 215 Common factor of 216 and 215 is 1 Since, both have only one common factor, i.c., 1. Therefore, 216 and 215 are co-prime numbers.

(f) Factors of 81 are 1, 3, 9, 27 and 81 Factors of 16 are 1, 2, 4, 8 and 16 Common factor of 81 and 16 is 1 Since, both have only one common factor, i.e., 1. Therefore, 81 and 16 are co-prime numbers.

Question 6.
A number is divisible by both 5 and 12. By which other number will that number be always divisible?
Solution:
Since 5 × 12 = 60. The number divisible by both 5 and 12, must also be divisible by 60.

Question 7.
A number is divisible by 12. By what other numbers will that number be divisible?
Solution:
Factors of 12 are 1, 2, 3, 4, 6 and 12.
Therefore, the number divisible by 12, will also be divisible by 1, 2, 3, 4 and 6.

MP Board Class 6th Maths Solutions

MP Board Class 6th Maths Solutions Chapter 3 Playing With Numbers Ex 3.3

Question 1.
Using divisibility tests, determine which of the following numbers are divisible by 2; by 3; by 4; by 5; by 6; by 8; by 9; by 10; by 11 (say, yes or no):

Solution:

Question 2.
Using divisibility tests, determine which of the following numbers are divisible by 4; by 8:
(a) 572
(b) 726352
(c) 5500
(d) 6000
(e) 12159
(f) 14560
(g) 21084
(h) 31795072
(i) 1700
(j) 2150
Solution:
(a) 572 is divisible by 4 as its last two digits are divisible by 4, but it is not divisible
by 8 as its last three digits are not divisible by 8.
(b) 726352 is divisible by 4 as its last two digits are divisible by 4 and it is also divisible by 8 as its last three digits are divisible by 8.
(c) 5500 is divisible by 4 as its last two digits are divisible by 4, but it is not divisible by 8 as its last three digits are not divisible by 8.
(d) 6000 is divisible by 4 as its last two digits are divisible by 4 and it is also divisible by 8 as its last three digits are divisible by 8.
(e) 12159 is not divisible by 4 and 8 as it is an odd number.
(f) 14560 is divisible by 4 as its last two digits are divisible by 4 and it is also divisible by 8 as its last three digits are divisible by 8.
(g) 21084 is divisible by 4 as its last two digits are divisible by 4, but it is not divisible by 8 as its last three digits are not divisible by 8.
(h) 31795072 is divisible by 4 as its last two digits are divisible by 4 and it is also divisible by 8 as its last three digits are divisible by 8.
(i) 1700 is divisible by 4 as its last two digits are divisible by 4, but it is not divisible by 8 as its last three digits are not divisible by 8.
(j) 2150 is not divisible by 4 as its last two digits are not divisible by 4 and it is not divisible by 8 as its last three digits are not divisible by 8.

Question 3.
Using divisibility tests, determine which of following numbers are divisible by 6:
(a) 297144
(c) 4335
(e) 901352
(f) 438750
(g) 1790184
(h) 12583
(i) 639210
(j) 17852
Solution:
(a) 297144 is divisible by 2 as its ones place is an even number place is an even number and it is also divisible by 3 as sum of its digits (= 27) is divisible by 3.
Since, the number is divisible by both 2 and 3. Therefore, it is also divisible by 6.

(b) 1258 is divisible by 2 as its ones place is an even number, but it is not divisible by 3 as sum of its digits (= 16) is not divisible by 3.
Since, the number is not divisible by both 2 and 3. Therefore, it is not divisible by 6.

(c) 4335 is not divisible by 2 as its ones place is not an even number, but it is divisible by 3 as sum of its digits (= 15) is divisible by 3.
Since, the number is not divisible by both 2 and 3. Therefore, it is not divisible by 6.

(d) 61233 is not divisible by 2 as its ones place is not an even number, but it is divisible by 3 as sum of its digits (= 15) is divisible by 3.
Since, the number is not divisible by both 2 and 3. Therefore, it is not divisible by 6.

(e) 901352 is divisible by 2 as its ones place is an even number, but it is not divisible by 3 as sum of its digits (= 20) is not divisible by 3.
Since, the number is not divisible by both 2 and 3. Therefore, it is not divisible by 6.

(f) 438750 is divisible by 2 as its ones place
is an even number and it is also divisible by 3 as sum of its digits (= 27) is divisible by 3.
Since, the number is divisible by both 2 and 3. Therefore, it is also divisible by 6.

(g) 1790184 is divisible by 2 as its ones place is an even number and it is also divisible by 3 as sum of its digits (= 30) is divisible by 3.
Since, the number is divisible by both 2 and 3. Therefore, it is also divisible by 6.

(h) 12583 is not divisible by 2 as its ones place is not an even number and it is also not divisible by 3 as sum of its digits (= 19) is not divisible by 3.
Since, the number is not divisible by both 2 and 3. Therefore, it is not divisible by 6.

(i) 639210 is divisible by 2 as its ones place is an even number and it is also divisible by 3 as sum of its digits (= 21) is divisible by 3.
Since, the number is divisible by both 2 and 3. Therefore, it is divisible by 6.

(j) 17852 is divisible by 2 as its ones place is an even number, but it is not divisible by 3 as sum of its digits (= 23) is not divisible by 3.
Since, the number is not divisible by both 2 and 3. Therefore, it is not divisible by 6.

Question 4.
Using divisibility tests, determine which of the following numbers are divisible by 11:
(a) 5445
(b) 10824
(c) 7138965
(d) 70169308
(e) 10000001
(f) 901153
Solution:
(a) In 5445, sum of the digits at odd places = 5 + 4 = 9
Sum of the digits at even places = 4 + 5 = 9
Difference of both sums = 9 – 9 = 0
Since the difference is 0. Therefore, the number is divisible by 11.

(b) In 10824, sum of the digits at odd places = 4 + 8 + 1 = 13
Sum of the digits at even places = 2 + 0 = 2
Difference of both sums = 13 – 2 = 11
Since the difference is divisible by 11.
Therefore, the number is divisible by 11.

(c) In 7138965, sum of the digits at odd places = 5 + 9 + 3 + 7 = 24
Sum of the digits at even places = 6 + 8 + 1 = 15
Difference of both sums = 24 – 15 = 9
Since the difference is neither 0 nor divisible by 11. Therefore, the number is not divisible by 11.

(d) In 70169308, sum of the digits at odd places = 8 + 3 + 6 + 0 = 17
Sum of tire digits at even places = 0 + 9 + 1 + 7 = 17
Difference of both sums = 17 – 17 = 0
Since the difference is 0. Therefore, the number is divisible by 11.

(e) In 10000001, sum of the digits at odd places = 1 + 0 + 0 + 0 = 1
Sum of the digits at even places =0 + 0 + 0 + 1 = 1
Difference of both sums = 1 – 1 = 0
Since the difference is 0. Therefore, the number is divisible by 11.

(f) In 901153, sum of the digits at odd places =3 + 1 + 0 = 4
Sum of the digits at even places = 5 + 1 + 9 = 15
Difference of both sums = 15 – 4 = 11
Since the difference is 11. Therefore, the number is divisible by 11.

Question 5.
Write the smallest digit and the greatest digit in the blank space of each of the following numbers so that the number formed is divisible by 3:
(a) _6724
(b) 4765 _2
Solution:
We know that a number is divisible by 3 if the sum of all digits is divisible by 3.
(a) The smallest digit will be 2.
∴ The number formed is 26724 and
2 + 6 + 7 + 2 + 4 = 21, which is divisible by 3.
And the greatest digit will be 8.
∴ The number formed is 86724 and
8 + 6 + 7 + 2 + 4 = 27, which is divisible by 3.

(b) The smallest digit will be 0.
∴ The number formed is 476502 and
4 + 7 + 6 + 5 + 0 + 2 = 24, which is divisible by 3.
And the greatest digit will be 9.
∴ The number formed is 476592 and
4 + 7 + 6 + 5 + 9 + 2 = 33, which is divisible by 3.

Question 6.
Write a digit in the blank space of each of the following numbers so that the number formed is divisible by 11 :
(a) 92 _ 389
(b) 8 _ 9484
Solution:
(a) We know that a number is divisible by 11 if the difference of the sum of the digits at odd places and that of even places is either 0 or divisible by 11.
The number formed is 928389
Sum of digits at odd places = 9 + 3 + 2 = 14
Sum of digits at even places = 8 + 8 + 9 = 25
Their difference = 25 – 14 = 11, which is divisible by 11.

(b) We know that a number is divisible by 11 if the difference of the sum of the digits at odd places and that of even places is either 0 or divisible by 11.
The number formed is 869484 Sum of digits at odd places = 4 + 4 + 6 = 14
Sum of digits at even places = 8 + 9 + 8 = 25
Their difference = 25 – 14 = 11, which is divisible by 11.

MP Board Class 6th Maths Solutions

MP Board Class 6th Special Hindi व्याकरण

संज्ञा

परिभाषा-किसी व्यक्ति, जाति, वस्तु, स्थान, गुण एवं भाव के नाम को संज्ञा कहते हैं। जैसे- रजनीकान्त (व्यक्ति), घोड़ा (जाति), कुर्सी (वस्तु), आगरा (स्थान), पवित्रता (गुण)।

संज्ञा के भेद-संज्ञा के निम्नलिखित तीन भेद होते हैं-

1. जातिवाचक-जिस संज्ञा से एक जाति के प्राणियों या पदार्थों का बोध होता है, उसे जातिवाचक संज्ञा कहते हैं। यथा- नदी, नगर, नहर, भोज, फूल आदि। जातिवाचक संज्ञा के अन्तर्गत दो संज्ञाएँ और मानी जाती हैं जो क्रमशः समुदायवाचक एवं द्रव्यवाचक संज्ञाएँ कहलाती हैं।
   • समुदायवाचक-एक प्रकार की वस्तुओं के समूह का बोध कराने वाली संज्ञा समुदायवाचक संज्ञा कहलाती है। यथा-सभा, सोना, कक्षा आदि।
   • द्रव्यवाचक-धातुओं के नाम को द्रव्यवाचक कहा जाता है, यथा-मिट्टी, चाँदी, सोना, ताँबा, लोहा आदि।
2. व्यक्तिवाचक-जिस संज्ञा से किसी खास व्यक्ति, वस्तु या स्थान का बोध होता है। उसे हम व्यक्तिवाचक संज्ञा कहते हैं, यथा-हिमालय, गंगा, आगरा, निष्ठा, अक्षय कुमार आदि।
3. भाववाचक-जिस संज्ञा से किसी गुण, दशा, स्वभाव अथवा व्यापार का बोध होता है, उसे भाववाचक संज्ञा कहते हैं, यथा-भलाई, अहिंसा, पवित्रता, शत्रुता, बालकपन।

सर्वनाम

परिभाषा-जो शब्द संज्ञा के स्थान पर प्रयोग में लाये जाते हैं, उन्हें हम सर्वनाम कहते हैं।

सर्वनाम के भेद-सर्वनाम के निम्नलिखित छः भेद होते-

1. पुरुषवाचक सर्वनाम-वह सर्वनाम जो किसी व्यक्ति के लिए प्रयुक्त होता है, पुरुषवाचक सर्वनाम कहलाता है। जैसे-मैं, तू, तुम, यह, वह। पुरुषवाचक सर्वनाम तीन प्रकार के होते हैं-
   • उत्तम पुरुष-बोलने वाला या लिखने वाला अपने नाम के बदले जिस सर्वनाम का प्रयोग करता है, उसे उत्तम पुरुष कहते हैं। जैसे- मैं, हम।
   • मध्यम पुरुष-जिससे बात की जाए अथवा जिसे सम्बोधित किया जाए, उसके नाम के बदले प्रयुक्त सर्वनाम को मध्यम पुरुष कहते हैं। जैसे-तू, तुम, आप।
   • अन्य पुरुष-जिसके बारे में बात करते हैं या लिखते हैं उसके नाम के बदले प्रयुक्त सर्वनाम को अन्य पुरुष सर्वनाम कहते हैं। जैसे- यह, ये, वह, वे। ‘यह’ और ‘ये’ समीपस्थ अन्य पुरुष सर्वनाम हैं। तथा ‘वह’ और ‘वे’ दूरस्थ अन्य पुरुष सर्वनाम हैं।
2. निश्चय वाचक सर्वनाम-वे सर्वनाम हैं जो किसी निश्चित व्यक्ति या वस्तु की ओर संकेत करते हैं। जैसे- यह, वह।
3. अनिश्चय वाचक सर्वनाम-वे सर्वनाम जो किसी अनिश्चित व्यक्ति या वस्तु के लिए प्रयुक्त होते हैं। जैसे-कोई, कुछ।
4. प्रश्नवाचक सर्वनाम-वे सर्वनाम जिनका प्रयोग किसी व्यक्ति या वस्तु के सम्बन्ध में प्रश्न पूछने के लिए होता है। जैसे-कौन, क्या।
5. निजवाचक सर्वनाम-जो सर्वनाम कर्ता के साथ अपनापन (निजत्व) बनाने के लिए आता है, उसे निजवाचक सर्वनाम कहा जाता है। जैसे-आप, खुद, स्वयं।
6. सम्बन्धवाचक सर्वनाम-जो सर्वनाम साथ में आए किसी अन्य उपवाक्य में प्रयुक्त संज्ञा या सर्वनाम से सम्बन्ध बताने के लिए प्रयोग किए जाते हैं, सम्बन्ध सूचक सर्वनाम कहलाते हैं। जैसे- जो, वे, जो-वह, जो-सो।

कारक एवं विभक्ति जिस शब्द द्वारा संज्ञा या सर्वनाम का सम्बन्ध सिद्ध होता है उसे कारक कहते हैं। जिस चिन्ह को कारक द्वारा ज्ञात किया जाता है उसमें उसी प्रकार की विभक्ति का प्रयोग होता है। जैसे-कर्ता ‘ने’ प्रथमा विभक्ति, कर्म’को’ द्वितीया विभक्ति आदि। उदाहरण के लिए-राम ने रावण को मारा। रामः रावण हतवान ‘ने’, ‘को’ और ‘से’ तीन विभक्तियाँ हैं तथा इन्हीं से वाक्य के कारकों का निर्धारण होता है।

हिन्दी में कारकों की संख्या आठ मानी गई है-

1. कर्ता कारक-वाक्य में करने वाले को कर्ता कारक कहा जाता है। इसका चिन्ह ‘ने’ होता है।
2. कर्म कारक-जिस वस्तु पर क्रिया के व्यापार का फल पड़े, उसे हम कर्म कारक कहते हैं। इसका चिन्ह “को’ है, यथा-तुमने कुत्ते को मारा। (विभक्ति को’)
3. करण कारक-कर्ता जिसकी सहायता से कोई व्यापार पूर्ण करता है, उसे हम करण कारक कहते हैं। जैसे-राम ने रावण को बाण से मारा। (विभक्ति-से)
4. सम्प्रदान कारक-कर्ता जिसके लिए कोई कार्य करता है, उसे हम सम्प्रदान कारक कहते हैं। यथा-कनिष्ठ पल्लव के लिए पेड़े लाता है। (विभक्ति-को, के, लिए)
5. अपादान कारक-जिसका अलग होना व्यक्त हो।। जैसे-यह बालक छत से गिरता है। (विभक्ति-से)
6. सम्बन्ध कारक-जिसके द्वारा संज्ञा का सम्बन्ध या अधिकार स्थापित किया जाता है। उसे हम सम्बन्ध कारक कहते हैं। यथा-नरेन्द्र कुमार का घर है। (विभक्ति-का, की, के)
7. अधिकरण कारक-संज्ञा के जिस रूप से क्रिया के आधार का ज्ञान हो उसे अधिकरण कारक कहते हैं। जैसे कोयल आम की डाली पर बैठी है। (विभक्ति-मैं, पै, पर)
8. सम्बोधन कारक-जिसके द्वारा किसी को बुलाया या सचेत किया जाता है वहाँ पर सम्बोधन कारक होता है। यथा-हे अक्षय उठो। (विभक्ति-हे, अरे, अहो)

विशेषण

परिभाषा-जो शब्द संज्ञा या सर्वनाम की विशेषता बतलाते हैं, उन्हें हम विशेषण कहते हैं, यथा-नीला पैन, अच्छी पुस्तक। यहाँ पर ‘नीला’ और ‘अच्छी’ क्रमशः पैन और पुस्तक संज्ञा की विशेषता प्रकट कर रहे हैं, अतः ये दोनों विशेषण हैं।

विशेष्य-जिन शब्दों की विशेषता बताई जाती है, वे शब्द विशेष्य होते हैं, जैसे सफेद गाय। ‘गाय’ शब्द विशेष्य है।

विशेषण के भेद-विशेषण निम्नलिखित छः प्रकार के होते हैं-

1. गुण वाचक-जिन शब्दों से संज्ञा या सर्वनाम के गुणों का बोध हो उन्हें हम गुण वाचक विशेषण कहते हैं। यथा-यह तस्वीर सुन्दर है। इस वाक्य में ‘सुन्दर तस्वीर संज्ञा का गुण बता रहा है। अत: यहाँ गुण वाचक विशेषण हुआ। यथा-मोटा आदमी, पतला लड़का, पीली गाय, लाल बकरी।
2. संख्या वाचक-जो शब्द संज्ञा की संख्या का ज्ञान कराता है, उसे हम संख्या वाचक विशेषण कहते हैं, जैसे-दस आदमी, चार पुस्तक आदि।
3. परिमाण वाचक-जिस शब्द से किसी वस्तु के परिमाण का बोध होता है, उसे हम परिमाण वाचक विशेषण कहते हैं, यथा-तुम्हारे पास कितने रुपये हैं, थोड़ा पानी पिओ। जरा, काफी, बहुत, थोड़ा आदि परिमाण वाचक विशेषण हैं।
4. संकेत वाचक-जो शब्द संज्ञा की ओर संकेत करें, उन्हें हम संकेत वाचक विशेषण कहते हैं, यथा-आप इस पुस्तक को अवश्य पढ़ें। इस वाक्य में इस’ शब्द ‘पुस्तक’ संज्ञा की ओर संकेत करता है, अतः यहाँ संकेत वाचक विशेषण हुआ।
5. व्यक्ति वाचक-जिन विशेषणों का निर्माण व्यक्ति वाचक संज्ञाओं से होता है, उन्हें हम व्यक्ति वाचक विशेषण कहते हैं यथा-इलाहाबादी अमरूद, कश्मीरी सेव।
6. विभाग वाचक-जिन विशेषणों के माध्यम से पृथकता का बोध हो, उन्हें विभाग वाचक विशेषण कहते हैं; यथा-प्रत्येक छात्र को पारितोषक दो। इस वाक्य में ‘प्रत्येक’ शब्द से अलग-अलग छात्रों का बोध होता है, अतः यहाँ विभाग वाचक विशेषण हुआ।

क्रिया विशेषण

परिभाषा-जिन शब्दों से क्रिया के अर्थ में विशेषता आती है, उन्हें हम क्रिया विशेषण कहते हैं, यथा-कम खेलो, जल्दी जाओ-में कम और जल्दी दोनों ही क्रिया विशेषण हैं।

क्रिया विशेषण के भेद-क्रिया विशेषण निम्नलिखित पाँच प्रकार के होते हैं-

1. गुण वाचक क्रिया विशेषण-जो क्रियाएँ विशेषण के गुण प्रदर्शित करती हैं, उन्हें गुण वाचक क्रिया विशेषण कहते हैं; जैसे-कोयल बहुत मधुर बोलती है। मोहन जोर से बोलता है। (मधुर, जोर, बहुत)।
2. परिमाण वाचक क्रिया विशेषण-जिन शब्दों से क्रिया के परिमाण का ज्ञान होता है, वहाँ परिमाण वाचक क्रिया-विशेषण माना जाता है। यथा-‘ज्यादा लिखो’ में ज्यादा’ परिमाण वाचक क्रिया विशेषण है।
3. स्थान वाचक क्रिया विशेषण-जिन शब्दों के द्वारा क्रिया होने का स्थान ज्ञात हो वहाँ स्थान वाचक क्रिया विशेषण होता है। यथा-‘पल्लव कहाँ रहता है’, में कहीं स्थान वाचक क्रिया विशेषण है।
4. रीति वाचक क्रिया विशेषण-जिन शब्दों से क्रिया होने की रीति या ढंग का ज्ञान हो वहाँ रीति वाचक क्रिया विशेषण होता है। यथा-अक्षय कुमार सहसा आ गया-में ‘सहसा’ रीति वाचक क्रिया विशेषण है।
5. काल वाचक क्रिया विशेषण-जिन शब्दों से क्रिया के घटित होने की अवधि का निश्चय हो, यथा-कल यहाँ महात्मा गाँधी आये थे-इस वाक्य में ‘कल’ काल वाचक क्रिया विशेषण है। विशेषण और क्रिया विशेषण में अन्तर विशेषण के द्वारा किसी संज्ञा या सर्वनाम की विशेषता बताई जाती है जबकि क्रिया विशेषण के द्वारा क्रिया के अर्थ में विशेषता को स्पष्ट किया जाता है। जैसे-
   • लाल कमीज, नीला कुर्ता इन शब्दों में लाल और नीला कमीज और कुर्ता की अच्छाई बताते हैं, अत: लाल और नीला शब्द विशेषण हैं।
   • जल्दी लिखो, तेज चलो में जल्दी और तेज-दोनों लिखो और चलो क्रिया के अर्थ की विशेषता बताते हैं। इसलिए जल्दी और तेज दोनों ही क्रिया विशेषण हैं।

क्रिया

परिभाषा-जिन शब्दों से किसी कार्य का करना या होना पाया जाये, उन्हें क्रिया करते हैं। क्रिया के अभाव में कोई कार्य पूर्ण नहीं होता। यथा-कनिष्क खेलता है, पल्लव पुस्तक खरीदता है, आदि वाक्यों में खेलता है, खरीदता है शब्दों से खेलने तथा खरीदने की क्रिया का बोध होता है।

1. सकर्मक क्रिया-जिस क्रिया के साथ कर्म प्रयुक्त हो। जैसे-पल्लव आम खरीदता है-इस वाक्य में खरीदना क्रिया का फल आम पर पड़ रहा है, अतः खरीदना सकर्मक क्रिया है।
2. अकर्मक क्रिया-जिस क्रिया का कोई कर्म न हो। जैसे-अक्षय पढ़ता है।

शब्द ज्ञान
प्रयोग के विचार से शब्दों के दो मुख्य भेद हैं-
(क) विकारी,
(ख) अविकारी।

(क) जिन शब्दों के रूप लिंग, वचन और कारक के आधार पर बदल जाते हैं, उन्हें विकारी शब्द कहते हैं; जैसे-लड़का, लड़की, लड़कों। अच्छा, अच्छे, अच्छों, जाता, जाती, जाते, मैं, मुझे, तुम, तुम्हारा, हम, हमें, हमारा आदि।
(ख) जिन शब्दों में लिंग, वचन और कारक के द्वारा कोई परिवर्तन नहीं होता अर्थात् जिनका रूप एक-सा रहता है, उन्हें अविकारी शब्द कहते हैं; जैसे-यहाँ, वहाँ, प्रतिदिन, परन्तु, भी, हो, आज आदि।

अविकारी शब्दों को अव्यय शब्द भी कहते हैं। अविकारी शब्द या अव्यय को मुख्य रूप से चार भेदों में बाँटा गया है। वे भेद हैं-

1. क्रिया-विशेषण,
2. सम्बन्ध बोधक,
3. समुच्चय बोधक
4. विस्मयादिबोधक।

(1) क्रिया विशेषण ऊपर पढ़ चुके हैं।
(2) सम्बन्ध बोधक-जो अव्यय संज्ञा या सर्वनाम का सम्बन्ध अन्य शब्दों से जोड़ते हैं, उन्हें सम्बन्ध बोधक कहते हैं।

जैसे-
(क) सुमित बाग में खेल रहा है।
(ख) पेड़ के ऊपर तोते हैं।
(ग) मेज के नीचे बिल्ली है।
(घ) जल के बिना जीवन कठिन है।
(ड.) चिराग तले अँधेरा रहता है।

इन वाक्यों में रेखांकित शब्द सम्बन्धबोधक अव्यय हैं। कुछ अन्य शब्द; जैसे-के लिए, के हेतु, के साथ, के मारे, के बाहर, के अन्दर, के आगे, के पीछे, के बिना, के द्वारा, के विरुद्ध, के अतिरिक्त, के बदले, के विपरीत, के अनुकूल की उपेक्षा भी अव्यय का अविकारी शब्द हैं।
(3) समुच्चय बोधक-दो शब्दों, वाक्यांशों या वाक्यों को आपस में जोड़ने वाले अविकारी शब्दों को समुच्चय बोधक कहते हैं, जैसे
(क) रवि और अशोक मित्र हैं।
(ख) तुम जाते हो या मैं जाऊँ।
(ग) यदि परिश्रम करोगे तो अवश्य सफल होगे। इन वाक्यों में रेखांकित शब्द समुच्चय बोधक अव्यय हैं।

(4) विस्मयादिबोधक-जो अव्यय शब्द विस्मय, हर्ष, शोक, घृणा आदि भावों को प्रकट करते हैं, उन्हें विस्मयादिबोधक
कहते हैं। विस्मयादिबोधक अव्यय के बाद विस्मय चिन्ह (!) लगता है।

जैसे-
(क) बाप रे ! इतना बड़ा साँप!
(ख) अरे ! तुम यहाँ आ गए।
(ग) शाबास ! आगे बढ़ते चलो।
(घ) हाय ! मार डाला।
(ड.) वाह ! तुमने तो कमाल कर दिया। रेखांकित शब्द विस्मयबोधक अव्यय हैं।

शब्द वर्ग के आधार पर हिन्दी भाषा में निम्नलिखित पाँच प्रकार के शब्द हैं-

1. तत्सम शब्द-संस्कृत भाषा के ऐसे शब्द जो हिन्दी में ज्यों के त्यों प्रचलित हैं, तत्सम शब्द कहलाते हैं। जैसे-दुग्ध, हस्त, स्नेह, सूर्य, चन्द्र, अग्नि। .
2. तद्भव शब्द-तत्सम शब्दों में विकार आने से जब उनका शब्द परिवर्तित हो जाता है, तो वे तद्भव शब्द कहलाते हैं। जैसे- दूध, हाथ, स्नेह, सूरज, चाँद आदि।
3. देशज शब्द-ऐसे शब्द जिनकी व्युत्पत्ति का ठीक से पता नहीं है और जो क्षेत्रीय बोलियों से हिन्दी में आ गये हैं, देशज शब्द कहलाते हैं। जैसे- पेड़, खिड़की, गाड़ी, माखन, चिड़िया, जूता, कटोरा, लोटा, पगड़ी।
4. विदेशी शब्द-अन्य देशों की भाषाओं से हिन्दी में आए शब्द को विदेशी शब्द कहते हैं। जैसे-स्टेशन, स्कूल, पिस्तौल, बोतल, पाजामा, दुकान, तमाशा।
5. संकर-ऐसे शब्द जो तत्सम, तद्भव, देशज एवं अन्य किसी विदेशी भाषा से मिलकर बनते हैं, संकर शब्द कहलाते हैं। जैसे-डबल रोटी, रेलगाड़ी, अजायबघर।

कुछ प्रमुख तत्सम/तद्भव शब्द

उपसर्ग

परिभाषा-वे शब्द या शब्दांश जो शब्दों के पूर्व (पहले) जुड़कर नये शब्द बनाते हैं, उपसर्ग कहलाते हैं। जैसे-‘अ’ उपसर्ग से अज्ञान, असफल आदि शब्द बनते हैं।

उपसर्ग लगाने से शब्द का अर्थ बदल जाता है। जैसे-डर का अर्थ भय है किन्तु इसके आगे ‘नि’ उपसर्ग लगाकर निडर शब्द बनता है जिसका अर्थ है ‘न’ डरने वाला।

उपसर्ग से बने हुआ शब्द निमन प्रकार के हैं-

प्रत्यय

परिभाषा-वे शब्द या शब्दांश जो किसी शब्द के अन्त में लगाने से नया शब्द बनाते हैं, प्रत्यय कहलाते हैं। जैसे-गाड़ी शब्द में ‘वान’ प्रत्यय लगाने से ‘गाड़ीवान’ शब्द बना है। प्रत्यय लगाने से शब्द का अर्थ परिवर्तित हो जाता है। जैसे-मोटा में यदि ‘पा’ प्रत्यय लग जाये तो मोटापा हो जाता है। कुछ प्रत्यय निम्नलिखित हैं-

काल

परिभाषा-“क्रिया के जिस रूप से उसके होने अथवा करने का समय ज्ञात होता है, उसे काल कहते हैं।
काल के भेद-मुख्य रूप से काल के निम्नलिखित भेद होते हैं

1. वर्तमान काल-जिस काल में क्रिया का वर्तमान समय में होना पाया जाता है, उसे वर्तमान काल कहते हैं।
   उदाहरण के लिए-मैं पढ़ रहा हूँ।
2. भूतकाल-जिस काल में क्रिया का बीते हुए समय में होना पाया जाय, उसे भूतकाल कहते हैं।
   उदाहरण के लिए-मैं पढ़ रहा था।
3. भविष्य काल-जिस काल में क्रिया का आने वाले समय में होना पाया जाता है,उसे भविष्य काल कहते हैं।
   उदाहरण के लिए-मैं पढ़ रहा हूँगा।

वाक्य प्रकार

वाक्य विचार
परिभाषा-शब्दों के उस क्रमबद्ध समूह को वाक्य कहते हैं, जिससे अर्थ पूरी तरह से स्पष्ट हो जाए। जैसे-‘गंगातट पर स्थित एक पाठशाला में आचार्य ध्रुवनारायण पढ़ाया करते थे।’

भाव और अर्थ को स्पष्ट करने वाला वाक्य सफल कहा जाता है। सरल और सुन्दर वाक्य में अग्रलिखित गुण होने चाहिए

1. आकांक्षा,
2. योग्यता,
3. आसक्ति या सन्निधि,
4. पदक्रम,
5. अन्विति,
6. सार्थकता।

मुख्य रूप से वाक्य के निम्नलिखित तीन प्रकार होते हैं-

1. विधिवाचक वाक्य-जिन वाक्यों से किसी बात के होने का बोध होता है, विधिवाचक वाक्य कहलाते हैं।
   उदाहरण के लिए-
   • जुम्मन शेख की एक बूढ़ी खाला थी।
   • मैं आज वहाँ जाऊँगा।
2. निषेधवाचक वाक्य-जिन वाक्यों में किसी बात के न होने अथवा न करने का बोध होता है, निषेधवाचक वाक्य कहलाते हैं।
   उदाहरण के लिए-
   • मैं स्कूल नहीं जाऊँगा।
   • उसने खाना नहीं खाया।
3. आज्ञावाचक वाक्य-जिन वाक्यों से किसी भी प्रकार की आज्ञा का बोध होता है, आज्ञावाचक वाक्य कहलाते हैं।
   उदाहरण के लिए-
   1. वहाँ कौन है ?
   2. क्या तुम वहाँ नहीं गये ?

लिंग

परिभाषा-जिस संज्ञा शब्द से किसी स्त्री अथवा पुरुष जाति का ज्ञान होता है, उसे हम लिंग कहते हैं। हिन्दी में लिंग के निम्नलिखित दो भेद हैं

1. स्त्रीलिंग-जिस संज्ञा शब्द से स्त्री जाति का बोध होता है, उसे हम स्त्रीलिंग कहते हैं। यथा- गाय, लड़की, बिल्ली।
2. पुल्लिंग-जिस संज्ञा शब्द से पुरुष जाति का बोध होता है। उसे हम पुल्लिंग कहते हैं, यथा-अक्षयकुमार, कनिष्क, कुत्ता, बैल, लड़का।

वचन

परिभाषा-“संज्ञा अथवा सर्वनाम के जिस रूप से वस्तु अथवा प्राणी की संख्या का बोध होता है, उसे वचन कहते हैं।

वचन के भेद-मुख्य रूप से वचन के निम्नलिखित दो भेद होते हैं-

1. एकवचन-संज्ञा अथवा सर्वनाम का वह रूप जिससे एक ही वस्तु अथवा प्राणी का बोध होता है, एकवचन कहलाता है। जैसे-वायु, पुस्तक, मटका, लड़का आदि।
2. बहुवचन-संज्ञा अथवा सर्वनाम का वह रूप जिससे एक से अधिक वस्तु अथवा प्राणी का बोध होता है, उसे बहुवचन कहते हैं। – जैसे- गायें, पुस्तकें, मटके, लड़के आदि।

सन्धि
परिभाषा-दो वर्णों के मेल से होने वाले विकार को संधि कहते हैं। यथा–रमेश में = रमा + ईश (आ + इ = ए हो गया)।

सन्धि के भेद-सन्धि के निम्नलिखित तीन भेद होते हैं-
1. स्वर संधि-दो स्वरों के परस्पर मेल से होने वाले विकार को स्वर संधि कहते हैं। यथा-हिमालय में, हिम + आलय = अ + आ = आ हो गया।

उदाहरण-

1. सूर्य + अस्त (अ + अ = आ) = सूर्यास्त।
2. कवि + इन्द्र (इ + इ = ई) = कवीन्द्र।
3. नदी + ईश (ई + ई = ई) = नदीश।
4. सु + उक्ति (उ + उ = ऊ) = सूक्ति।
5. लघु + ऊर्मि (उ+ ऊ = ऊ) लघूर्मि।

उपर्युक्त उदाहरणों में दर्शाया गया है कि जब दो सवर्ण (समान वर्ण अर्थात् अ, आ के साथ अ या आ हो) हस्व या दीर्घ स्वर परस्पर निकट होने के कारण मिल जाते हैं, तो दोनों के मिलने पर दीर्घ स्वर हो जाता है।

2. व्यंजन संधि-व्यंजन के साथ स्वर अथवा व्यंजन के मेल को व्यंजन संधि कहते हैं।

• यथा-सत् + जन = सज्जन।
• जगत् + नाथ = जगन्नाथ।

3. विसर्ग संधि-विसर्ग के साथ स्वर अथवा व्यंजन के मेल को विसर्ग संधि कहते हैं।
यथा-

• निः + फल = निष्फल।
• मनः + हर = मनोहर,
• तेजः + मय = तेजोमयः,
• निः + धन = निर्धन।

समास

परिभाषा-दो शब्दों को मिलाकर जो नया पद बनता है वह समास कहलाता है।

जैसे-
राजपुत्र = राजा का पुत्र ।

समास के भेद-समास के निम्नलिखित छः भेद होते हैं-

1. तत्पुरुष समास-जिस समास में प्रथमा से लेकर सप्तमी तक विभक्ति का लोप हो, वहाँ तत्पुरुष समास होता है।
जैसे-

• राजमाता = राजा की माता।
• राज पुत्र = राजा का पुत्र।

2. कर्मधारय समास-विशेषण एवं विशेष्य के योग से बने समास को कर्मधारय कहते हैं,
जैसे-

• नील कमल, काला घोड़ा, लाल गुलाब आदि।

3. द्वन्द्व समास-इसमें दो पदों के बीच और का लोप होता है।
जैसे-

• राम-सीता = राम और सीता।
• लाभ-हानि = लाभ और हानि।

4. द्विगु समास-इसमें पहला शब्द संख्यावाचक होता है।
जैसे-

• नवरत्न = नव रत्नों का समूह;
• चौराहा = चार राहों का समूह आदि।

5. बहुब्रीहि समास-जिसमें अन्य अर्थ प्रधान हो।
जैसे-

• दशानन = दश हैं आनन जिसके अर्थात् रावण
• चन्द्रशेखर = चन्द्रमा है शिखर पर जिसके अर्थात् शंकर जी।

6. अव्ययी भाव समास-जिस पद में प्रथम पद अव्यय हो।
जैसे-

• यथाशक्ति = शक्ति के अनुसार;
• प्रतिदिन = दिन-दिन आदि।

मुहावरे

परिभाषा-जब वाक्य में किसी शब्द या शब्द-समूह का सामान्य अर्थ न लेकर उसका अन्य विशेष अर्थ लिया जाता है, तब उसे मुहावरा कहते हैं। जैसे-‘पेट में चूहे कूदना’ का अर्थ है-‘भूख लगना’। इसका वाक्य प्रयोग होगा-‘आज तो मेरे पेट में चूहे कूद रहे हैं।’

कुछ प्रमुख मुहावरे
(अर्थ व प्रयोग सहित)
1. बगुलों में हंस-मूों में बुद्धिमान। आजकल कपट वेषधारी मनुष्यों की वजह से बगुलों में हंस की परख कठिन है।
2. हृदय पर साँप लेटना-जलन से दुःखी होना। कारगिल के मोर्चे पर भारत से परास्त होने पर पाकिस्तान के हृदय पर साँप लोट गया।
3. खून की नदी बहाना-बहुतों को मार गिराना। सम्राट अशोक ने कलिंग के युद्ध में खून की नदी बहा दी।
4. प्राण फूंकना-उत्साहित करना। पूर्व प्रधानमन्त्री लाल बहादुर शास्त्री ने विगत भारत-पाक युद्ध में सैनिकों में नये प्राण फूंक दिए। ‘
5.कलेजा धड़कना-व्याकुल होना। अनहोनी की आशंका से मेरा कलेजा धड़क रहा है।
6. मंत्र मुग्ध-अत्यधिक वश में। रामायण की चौपाइयों को सुनकर लोग मंत्र मुग्ध हो जाते हैं।
7. छाती चौड़ी होना-खुशी या स्वाभिमान का अनुभव होना। भारतीय सैनिकों के शौर्यपूर्ण कारनामों से देशवासियों की छाती चौड़ी हो जाती है।
8. पीठ ठोंकना-शाबासी देना, जोश भरना। अक्षय कुमार परीक्षा में प्रथम श्रेणी के अंक लेकर उत्तीर्ण हुआ है, अत: उसकी पीठ ठोंकनी चाहिए।
9. दस्तक देना-खटखटाना। असमय किसी के घर जाकर दस्तक देना बुरी बात है।
10. गोद सूनी होना-संतान का मरना। भारत-पाक युद्ध में न जाने कितनी माँ-बहिनों की गोद सूनी हो गई।
11. कार्य सिद्ध होना-काम सम्पन्न होना। भगवान की कृपा से ही मेरी पुत्री के विवाह का कार्य सफलतापूर्वक सिद्ध हो गया।
12. जीवन से हाथ धोना-जिन्दगी गँवाना। भीड़ भरी सड़क पर असावधानी से चलने की वजह से कभी-कभी जीवन से हाथ धोना पड़ता है।
13. आँख में खटकना-बुरा लगना। आलसी मनुष्य सबकी आँखों में खटकते हैं।
14. अवस्था ढलना-वृद्ध होना। अवस्था ढलने पर हाथ-पाँव शिथिल हो जाते हैं।
15. साक्षात् चण्डी सी-बहुत अधिक गुस्से में। युद्ध के मैदानी में झाँसी की रानी साक्षात् चण्डी का रूप धारण किए हुए थी।
16. मन मोह लेना-आकर्षित करना। संगीत की मधुर ध्वनि सबका मन मोह लेती है।
17. दम लेना-परिश्रम के बाद सुस्ताना। कठिन श्रम के बाद दम लेना आवश्यक है।
18. माँग का सिन्दूर पोंछना-किसी के पति को मौत के घाट उतारना। कलिंग के युद्ध में अनेक माँ-बहिनों की माँग का सिन्दूर पोंछ दिया गया।
19. भाग्य पर इठलाना-स्वयं पर गर्व करना। ओछे मनुष्य व्यर्थ में ही अपने भाग्य पर इठलाया करते हैं।
20. शीश चढ़ाना-जान कुर्बान करना। आजादी की लड़ाई में जाने कितने देश भक्तों ने अपने शीश चढ़ाकर अपने कर्तव्य का पालन किया।
21. खून में उबाल आना-उमंग का संचार होना। श्री लाल बहादुर के ओजमय भाषण से सैनिकों के खून में उबाल “आने लगा।
22. आँखों में खून उतरना-अत्यधिक क्रोध में भरना। मुगलों की ललकार सुनकर राणा प्रताप की आँखों में खून उतर आया।
23. सिर पर पाँव रखकर भागना-शीघ्रता से भागना। प्रधानाचार्य को आता देखकर शरारती छात्र सिर पर पाँव रखकर भागा।
24.खून पसीना एक करना-अथक परिश्रम करना। राम ने परीक्षा में उत्तीर्ण होने के लिये खून पसीना एक कर दिया।
25. हाथ पैर जवाब देना-अधिक थक जाना। रमेश का घर ढूँढ़ते-ढूँढ़ते मेरे हाथ-पैर जवाब दे गये।
26. चकमा देना-धोखा देना। सीता को चकमा देकर उसका पड़ोसी पाँच सौ रुपये ले गया।
27. ईद का चाँद होना-बहुत समय बाद मिलना। रजनीकान्त बाहर नौकरी करने के कारण आजकल ईद का चाँद हो गया है।
28. हवाई किले बनाना-कल्पित योजनाएँ बनाना। आलसी आदमी बैठे-बैठे हवाई किले बनाता रहता है।
29. छक्के छुड़ाना-हरा देना। हल्दी घाटी के युद्ध में सैनिकों ने मुगल सेना के छक्के छुड़ा दिये।
30. कोल्हू का बैल-दिन-रात मेहनत करना। पिता की मृत्यु के पश्चात् मोहन परिवार का पेट भरने के लिये कोल्हू का बैल बना रहता है।
31. ईंट से ईंट बजाना-पूर्ण रूप से नष्ट कर देना। मराठों ने दुश्मन सेना की ईंट से ईंट बजा दी।
32. उड़ती चिड़िया पहचानना-मन का भाव जानना। ओमप्रकाश इतना चतुर है कि वह उड़ती चिड़िया को पहचान लेता है।
33. मिट्टी में मिलना-नष्ट होना। बाढ़ के कारण सैकड़ों भवन मिट्टी में मिल गये।
34. कुत्ते की मौत मरना-दयनीय दशा में मरना। कोढ़ होने के कारण वह कुत्ते की मौत मरा।
35.घी के दिये जलाना-बहुत अधिक खुशी मनाना। देश के आजाद होने पर लोगों ने घी के दिये जलाये।
36. कंधे डालना-हार स्वीकार करना। कैलाश मेले के अवसर पर अपार जन-समूह को देखकर पुलिस ने कंधे डाल दिये।
37. आग बबूला होना-गुस्सा करना। राम अपने पुत्र को जूआ खेलते देखकर आग बबूला हो गया।
38. कान का कच्चा होना-चुगलखोरों पर भरोसा करना। प्रधानाचार्य कान का कच्चा होने के कारण लिपिक की बात को सत्य मान लेते हैं।
39. आँख का तारा होना-बहुत प्यारा होना। श्रवण कुमार अपने माता-पिता की आँखों का तारा था।
40. आँखें दिखाना-गुस्सा करना। पिता ने जैसे ही आँखें दिखाई, पुत्र चुप हो गया।
41. उल्लू सीधा करना-मतलब पूरा करना। आजकल लोग अपना उल्लू सीधा करने में माहिर हैं।
42. सन्नाटा पसरना-शान्ति छाई रहना। विद्यालय में तो सन्नाटा पसरा हुआ है।
43. गप्पें लड़ाना-व्यर्थ की बातें करना। मुझे गप्पें लड़ाना अच्छा नहीं लगता है।
44. हाथ बँटाना-काम में सहायता करना। अब तो मोहन का पुत्र उसका हाथ बँटाने लगा है।
45. अन्धे की लाठी-एकमात्र सहारा। मोहन तो अपने पिता के लिए अन्धे की लाठी है।
46. अंगूठा दिखाना-इन्कार कर देना। रवि ने सहायता करने के नाम पर अंगूठा दिखा दिया।
47. फूटी आँख न सुहाना-बिल्कुल अच्छा न लगना। लक्ष्मण को राक्षस फूटी आँख भी न सुहाते थे।
48. आग में घी डालना-क्रोध को और भड़काना। लक्ष्मण की तीखी बातों ने परशुराम की आग में घी डाल दिया।
49. एक तो चोरी दूसरे सीना जोरी-अपराधी होकर अकड़ना। राधा ने श्याम की पेंसिल तोड़ दी। उलाहना देते हुए उसने एक तो चोरी की दूसरी सीना जोरी भी की।
50. तू डाल-डाल, मैं पात-पात-तू तो चतुर है, मगर मैं तुझसे भी चतुर हूँ। सही बात के लिए तू डाल-डाल मत डोल, मैं भी फिर पात-पात पर आऊँगा।

लोकोक्तियाँ
मुहावरे के समान वाक्यों में लोकोक्तियों का प्रयोग भी किया जाता है। लोकोक्ति शब्द ‘लोक’ और ‘उक्ति’ से मिलकर बना है। लोकोक्तियाँ सामाजिक जीवन के अनुभव के आधार पर बनती हैं। हम इनका प्रयोग आवश्यकता के अनुसार करते हैं। कहीं कथन की पुष्टि के लिए तो कहीं उपदेश देने के लिए। लोकोक्तियों का प्रयोग प्रभावकारी सिद्ध होता है। लोकोक्तियाँ मुहावरे की भाँति वाक्य का अंग नहीं होती। ये प्रायः पूर्ण वाक्य होती हैं। इन्हें ‘कहावत’ भी कहते हैं।

लोकोक्तियाँ विशेष सन्दर्भ में प्रयुक्त होती हैं और उनका विशेष अर्थ ही लिया जाता है; जैसे-‘कोयल होय न ऊजरी, सौ मन साबुन लाय। इसमें कोयल’ उसके जन्मजात गुण कालापन को प्रकट करता है, ऊजरी होना’ इस गुण के परिवर्तन को प्रकट करता है और ‘सौ मन साबुन लाय’ विभिन्न उपायों का बोध कराता है। यही विशेष अर्थ है। अतः पूरी लोकोक्ति का अर्थ है, ‘भिन्न-भिन्न उपायों से भी व्यक्ति का जन्मजात गुण या अवगुण बदला नहीं जा सकता।’

मुहावरा और लोकोक्ति में अंतर मुहावरे का प्रयोग वाक्यांश की भाँति किया जाता है जबकि लोकोक्ति का प्रयोग कथन के अंत में, स्वतन्त्र वाक्य के रूप में किया जाता है।

कुछ प्रमुख लोकोक्तियाँ
नीचे कुछ लोकोक्तियाँ व उनके अर्थ दिए गए हैं, इनका वाक्यों में प्रयोग कीजिए

1. अकेला चना भाड़ नहीं फोड़ सकता-कोई बड़ा काम अकेले नहीं किया जा सकता है।
   राम भला इतने बड़े खेत को एक दिन में कैसे जोत पाता ठीक ही है, अकेला चना भाड़ नहीं फोड़ सकता।
2. अधजल गगरी छलकत जाए-अल्पज्ञान वाला बहुत बढ़-चढ़कर बोलता है।
   आठवीं फेल राजू बात ऐसी करता है मानो दुनिया में सबसे बड़ा विद्वान वही है। किसी ने ठीक ही कहा है कि अधजल गगरी छलकत जाए।
3. आम के आम गुठलियों के दाम-एक काम से दो लाभ।
   सरिता छोटे बच्चों को ट्यूशन पढ़ाकर पैसे भी कमा लेती है और उसके ज्ञान में भी वृद्धि होती है। ठीक ही कहा है, आम के आम गुठलियों के दाम।
4. जिसकी लाठी उसकी भैंस-बलवान की ही जीत होती है।
   गाँव के जमींदार ने गरीब अलगू की भूमि जबरन कब्जा ली। किसी ने ठीक ही कहा है, जिसकी लाठी उसकी भैंस।
5. होनहार बिरवान के होत चीकने पात-प्रतिभाशाली व्यक्तियों के लक्षण बचपन में ही प्रकट हो जाते हैं।
   प्रसिद्ध भारतीय गणितज्ञ रामानुजम् बचपन से ही गणित विषय में पारंगत थे। शायद ऐसे ही लोगों के लिए कहा जाता है, होनहार बिरवान के होत चीकने पात।
6. कंगाली में आटा गीला-मुसीबत में मुसीबत आना।
   बड़ी कठिनाई से तो रवि ने अपने पुत्र को पढ़ने भेजा, ऊपर से वह फेल हो गया; तभी तो कहते हैं कंगाली में आटा गीला।

अलंकार

परिभाषा-कविता को सजाने वाले शब्द और अर्थ से युक्त वाक्यों को अलंकार कहते हैं। कुछ प्रमुख अलंकार हैं
यमक-
जहाँ एक शब्द के दो अर्थ होते हैं।

जैसे-
कनक कनक ते सौ गुनी मादकता अधिकाय।
वा खाये बौराय जग या पाये बौराय।

श्लेष-
जिसमें एक शब्द के कई अर्थ हैं,

जैसे-
पानी गये न ऊबरे मोती मानस चून।

यहाँ पानी शब्द के आब, प्रतिष्ठा और जल यह तीन अर्थ हैं।

उपमा-
जब एक वस्तु की दूसरी से तुलना की जाए वहाँ उपमा अलंकार होता है।

जैसे-
तवा समा तपती थी वसुन्धरा।
यहाँ जेठ की तपती धरती को तवे के समान बतलाया गया है।

रूपक-
जहाँ एक वस्तु को दूसरी वस्तु का रूप दिया जाये।

जैसे-
चरण कमल वन्दों हरि-राई।
यहाँ भगवान के चरणों को कमल का रूप दिया गया है।

अनुप्रास-
कविता में जहाँ एक ही वर्ण से प्रारम्भ होने वाले शब्दों का प्रयोग बार-बार किया जाता है, वहाँ अनुप्रास अलंकार होता है।
रघुपति राघव राजा राम। यहाँ ‘र’ वर्ण की आवृत्ति हुई है।

विराम चिन्ह

विराम का शाब्दिक अर्थ है रुकना, ठहराव या विश्राम। पढ़ते – वक्त शब्दों या वाक्य के आखिर में रुकने के हेतु प्रयोग होने वाले चिन्हों को विराम कहा जाता है।

1. पूर्ण विराम-इसका चिन्ह (।) है। इसका प्रयोग वाक्य के अन्त में होता है।
2. अल्प विराम-इसका चिन्ह (,) है। यह शब्द के पश्चात् थोड़ी देर रुकने के लिए प्रयुक्त होता है। यथा-कनिष्क, पल्लव और अक्षय बाजार गये।
3. अर्द्ध विराम-इसका चिन्ह (;) है। अर्द्ध विराम का प्रयोग अल्प विराम से कुछ अधिक देर तक रुकने के लिए होता है। यथा-पल्लव साल भर पढ़ा; परन्तु परीक्षा में सफल न हो सका।
4. संयोजक चिह्न-इसका चिन्ह (-) है। दो या दो से . अधिक शब्दों में सम्बन्ध व्यक्त करने के लिए संयोजक चिन्ह प्रयोग में लाया जाता है। यथा-सुख-दु:ख, धीरे-धीरे।
5. विस्मयादिबोधक-इनका चिन्ह (!) है। यह विस्मय सूचक शब्द या वाक्य के पश्चात् लगाया जाता है। यथा-हे राम! तुम कहाँ गए ? \
6. प्रश्नवाचक-इसका चिन्ह (?) है। प्रश्न पूछने की जगह इसका प्रयोग होता है। यथा-तुम कहाँ रहते हो ?
7. खाली स्थान-इसका चिन्ह (……..) है। इसका प्रयोग रिक्त स्थान के निमित्त होता है।
8. विवरण चिह्न-किसी बात को स्पष्ट करने के लिए (:) इसका प्रयोग होता है।
9. कोष्ठक-इसका चिन्ह () है। किसी का विभाजन करते समय कोष्ठकों में रखकर संख्या डालते चलते हैं। यथा-संज्ञा तीन प्रकार की होती है-
   • व्यक्तिवाचक,
   • जातिवाचक,
   • भाववाचक।
10. हंस पद या त्रुटिसूचक चिह्न (4)-जब वाक्य में लिखते समय कुछ अंश छूट जाता है तब हंस पद (A) का प्रयोग करते हैं।

पर्यायवाची शब्द

परिभाषा-“जिन शब्दों का अर्थ समान हो, उन्हें समानार्थी अथवा पर्यायवाची शब्द कहते हैं।
जैसे- फूल को पुष्प, कुसुम, सुमन, पुहुप आदि भी कहते

• कुछ प्रमुख पर्यायवाची शब्द
• अमृत-सोम, अमी, सुधा, पीयूष।
• अग्नि-आग, अनल, पावक, हुताशन।
• आकाश-गगन, नभ, अम्बर, व्योम।
• अश्व-हय, घोटक, तुरंग, सैन्धव।
• चन्द्रमा-सुधांशु, राकापति, सुधाकर, शशी।
• गंगा-सुरसरि, भागीरथी, देवनदी, त्रिपथगा।
• यमुना-अर्कजा, तरणिजा, कालिन्दी, रविसुता।
• पानी-नीर, अम्बु, वारि, तोय, जल।
• कमल-नीरज, अम्बुज, वारिज, जलज।
• मेघ-नीरद, अम्बुद, जलद, वारिद।
• समुद्र-वारिधि, सागर, पयोधि, नीरधि।
• असुर-दानव, दैत्य, निशाचर।
• इन्द्र-सुरपति, शचीपति, देवेन्द्र, शक्र।
• तालाब-तड़ाग, सरसी, सरोवर, सर।
• दिन-दिवस, वासर, दिवा, अहन।
• पवन-वायु, मरुत, समीर, वात।
• नदी-सरिता, तटिनी, नद, तरंगिणी।
• पर्वत-भूधर, गिरि, नग, महोदर।
• पृथ्वी-भू, भूमि, मही, धरा।
• फल-सुमन, पुष्प, प्रसून।
• राजा-भूपति, महीपति, नृप, महीप।
• रात-निशा, रैन, रजनी, रात्रि।
• सूर्य-भानु, दिनकर, दिवाकर, रवि।
• सोना-हाटक, स्वर्ण, कंचन।
• हाथी-गज, नाग, हसती, वारण।
• जंगल-वन, कानन, अरण्य।
• पेड़-वृक्ष, पादप, विटप, तरु।
• आँख-नेत्र, चक्षु, नयन।
• ईश्वर-परमात्मा, सर्वेश्वर, अन्तर्यामी, प्रभु।
• पुत्र-सुत, तात, आत्मज, बेटा, तनय।
• हिमालय-नगराज, पर्वतराज, गिरिराज, हिमगिरि।
• पुत्री-सुता, तनया, बेटी, आत्मजा।
• कर-गृह, निकेतन, आवास, निवास।
• हाथ-कर, भुजाग्र, हस्त। मित्र-सखा, सहचर, सुहृद।

विलोम शब्द

परिभाषा-“ऐसे शब्द जो किसी शब्द का विपरीत अर्थ बताते हैं, उन्हें विपरीतार्थी अथवा विलोम शब्द कहते हैं। जैसे-ऊँचा का विलोम शब्द नीचा है।

कुछ प्रमुख विलोम शब्द

वाक्यांश के लिए एक शब्द

परिभाषा-“वे शब्द जिन्हें पूरे वाक्य या किसी शब्द समूह के स्थान पर प्रयोग किया जाता है, अनेक शब्दों के लिए एक शब्द कहा जाता है। जैसे- ‘जिसे कोई डर न हो’ को हम शब्द संक्षेप में ‘निडर’लिख सकते हैं।

अव्यय

परिभाषा-वे शब्द जिनके रूप में लिंग, वचन व कारक आदि के कारण कोई परिवर्तन नहीं होता है, उन्हें अव्यय कहते हैं। जैसे-धीरे, दूर, परन्तु, शीघ्र लेकिन आदि।

अव्यय के भेद-मुख्य रूप से अव्यय के निम्नलिखित चार भेद होते हैं.

1. क्रिया विशेषण
2. सम्बन्ध बोधक
3. समुच्चय बोधक
4. विस्मयादि बोधक।

MP Board Class 6th Hindi Solutions

MP Board Class 6th Maths Solutions Chapter 3 Playing With Numbers Ex 3.1

Question 1.
Write all the factors of the following numbers:
(a) 24
(b) 15
(c) 21
(d) 27
(e) 12
(f) 20
(g) 18
(h) 23
(i) 36
Solution:
(a) 24 =1 × 24 = 2 × 12 = 3 × 8 = 4 × 6 = 6 × 4
∴ Factors of 24 are 1, 2, 3, 4, 6, 8, 12 and 24
(b) 15 = 1 × 15 = 3 × 5 = 5 × 3
∴ Factors of 15 are 1, 3, 5 and 15
(c) 21 = 1 × 21 = 3 × 7 = 7 × 3
∴ Factors of 21 are 1, 3, 7 and 21
(d) 27 = 1 × 27 = 3 × 9 = 9 × 3
∴ Factors of 27 are 1, 3, 9 and 27
(e) 12 = 1 × 12 = 2 × 6 = 3 × 4 = 4 × 3 = 6 × 2
∴ Factors of 12 are 1, 2, 3, 4, 6 and 12
(f) 20 = 1 × 20 = 2 × 10 = 4 × 5 = 5 × 4
∴ Factors of 20 are 1, 2, 4, 5, 10 and 20
(g) 18 = 1 × 18 = 2 × 9 = 3 × 6 = 6 × 3 = 9 × 2
∴ Factors of 18 are 1, 2, 3, 6, 9 and 18
(h) 23 = 1 × 23
∴ Factors of 23 are 1 and 23,
(i) 36 = 1 × 36 = 2 × 18 = 3 × 12 = 4 × 9 = 6 × 6
∴ Factors of 36 are 1, 2, 3, 4, 6, 9, 12, 18 and 36

Question 2.
Write first five multiples of:
(a) 5
(b) 8
(c) 9
Solution:
(a) 5 × 1 = 5, 5 × 2 = 10, 5 × 3 = 15, 5 × 4 = 20, 5 × 5 = 25
∴ First five multiples of 5 are 5,10,15, 20, 25.
(b) 8 × 1 = 8, 8 × 2 = 16, 8 × 3 = 24, 8 × 4 = 32,
8 × 5 = 40
∴ First five multiples of 8 are 8,16, 24, 32, 40.
(c) 9 × 1 = 9, 9 × 2 = 18, 9 × 3 = 27, 9 × 4 = 36,
9 × 5 = 45
∴ First five multiples of 9 are 9, 18, 27, 36, 45.

Question 3.
Match the items in column 1 with the items in column 2.

Solution:
(i) ➝
(b) ;
(ii) ➝ (d);
(iii) ➝ (a);
(iv) ➝ (f);
(v) ➝ (c)
(a) Multiples of 8 are 8, 16, 24, 32, 40, ….
(b) Multiples of 7 are 7, 14, 21, 28, 35, …..
(c) Multiples of 70 are 70,140, 210, ……
(d) Factors of 30 are 1, 2, 3, 5, 6, 10,15, 30.
(e) Factors of 50 are 1, 2, 5, 10, 25.
(f) Factors of 20 are 1, 2, 4, 5, 10, 20.

Question 4.
Find all the multiples of 9 upto 100.
Solution:
Multiples of 9 upto 100 are 9, 18, 27, 36, 45, 54, 63, 72, 81, 90, 99

MP Board Class 6th Maths Solutions

MP Board Class 6th Maths Solutions Chapter 14 Practical Geometry Ex 14.6

Question 1.
Draw ∠POQ of measure 75° and find its line of symmetry.
Solution:
Steps of construction :

(i) Draw a line l and mark a point O on it.
(ii) Place the pointer of the compasses at O and draw an arc of any radius which intersects the line l at Q.
(iii) Taking same radius, with centre Q, draw an arc which cuts the previous arc at B.
(iv) Join OB, then ∠BOQ = 60°.
(v) Taking same radius, with centre B, draw an arc which cuts the arc drawn in step
(ii) at C.
(vi) Draw bisector of ∠BOC which cuts the \(\widehat{B C}\) at D. Thus, ∠DOQ = 90°.
(vii) Draw OP as bisector of ∠DOB. Thus, ∠POQ = 75°.

Question 2.
Draw an angle of measure 147° and construct its bisector.
Solution:
Steps of construction :

(i) Draw OA.
(ii) With the help of protractor, draw ∠AOB = 147°.
(iii) Taking centre O and any convenient radius, draw an arc which intersects \(\overline{O A}\) and \(\overline{O B}\) at P and Q respectively.
(iv) Taking P as centre and radius more than half of PQ, draw an arc.
(v) Taking Q as centre and with the same radius, draw another arc which intersects the previous arc at R.
(vi) Join OR and produce it.
Thus, \(\overline{O R}\) is the required bisector of ∠AOB.

Question 3.
Draw a right angle and construct its bisector.
Solution:
Steps of construction :

(i) Draw \(\overline{O Q}\).
(ii) With the help of protractor draw ∠QOP = 90°
(iii) Taking O as centre and any convenient radius, draw an arc which intersect the \(\overline{O P}\) and \(\overline{O Q}\) at A and B respectively.
(iv) Taking B and A as centre and radius more than half of BA, draw two arcs which intersect each other at the point D.
(v) Join OD. Thus, \(\overline{O D}\) is the required bisector of ∠QOP.

Question 4.
Draw an angle of measure 153° and divide it into four equal parts.
Solution:
Steps of construction :

(i) Draw \(\overline{O A}\).
(ii) At O, with the help of a protractor, draw ∠AOB = 153°.
(iii) Draw \(\overline{O C}\) as the bisector of ∠AOB.
(iv) Again, draw \(\overline{O D}\) as the bisector of ∠AOC.
(v) Again, draw \(\overline{O E}\) as the bisector of ∠BOC.
(vi) Thus; \(\overline{O C}\), \(\overline{O D}\) and \(\overline{O E}\) divide ∠AOB in four equal parts.

Question 5.
Construct with ruler and compasses, angles of following measures:
(a) 60°
(b) 30°
(c) 90°
(d) 120°
(e) 45°
(f) 135°
Solution:
Steps of construction:
(a) 60°

(i) Draw \(\overline{O A}\)
(ii) Taking O as- centre and convenient radius, draw an arc, which intersects \(\overline{O A}\) at P.
(iii) Taking P as centre and same radius, draw an arc which cut the previous arc at Q.
(iv) Join OQ and produce it to B. Thus, ∠BOA is the required angle of 60°.

(b) 30°

(i) Draw \(\overline{O A}\).
(ii) Taking O as centre and convenient radius, draw an arc, which intersects \(\overline{O A}\) at P.
(iii) Taking P as centre and same radius, draw an arc which cut the previous arc at Q.
(iv) Join OQ and produce it to B. Thus, ∠BOA is the angle of 60°.
(v) Taking P as centre and radius more than half of PQ, draw an arc.
(vi) Taking Q as centre and with same radius, draw an arc which cut the previous arc at C.
(vii) Join OC. Thus ∠COA is the required angle of 30°.

(c) 90°

(i) Draw \(\overline{O A}\).
(ii) Taking O as centre and convenient radius, draw an arc, which intersects \(\overline{O A}\) at X.
(iii) Taking X as centre and same radius, draw an arc which cut the previous arc at Y.
(iv) Taking Y as centre and same radius, draw another arc intersecting the arc drawn in step (ii) at ∠.
(v) Taking Y and ∠ as centres and same radius, draw two arcs intersecting each other at S.
(vi) Join OS and produce it to form a ray OB. Thus, ∠BOA is required angle of 90°.

(d) 120°

(i) Draw \(\overline{O A}\).
(ii) Taking O as centre and convenient radius, draw an arc, which intersects \(\overline{O A}\) at P.
(iii) Taking P as centre and same radius, draw an arc which cut the previous arc at Q.
(iv) Taking Q as centre and same radius draw another arc intersecting the arc drawn in step (ii) at S.
(v) Join OS and produce it to D.
Thus, ∠AOD is the required angle of 120°.

(e) 45°

(i) Draw \(\overline{O A}\).
(ii) Taking O as centre and convenient radius, draw an arc, which intersects \(\overline{O A}\) at X. .
(iii) Taking X as centre and same radius, draw an arc which cut the previous arc at Y.
(iv) Taking Y as centre and same radius, draw another arc intersecting the arc drawn in step (ii) at Z.
(v) Taking Y and Z as centres and same radius, draw two arcs intersecting each other at S.
(vi) Join OS and produce it to B. Thus, ∠BOA is the angle of 90°.
(vii) Draw OM the bisector of ∠BOA.
Thus, ∠MOA is the required angle of 45°.

(f) 135°

(i) Draw \(\overline{P Q}\) and take a point O on it.
(ii) Taking O as centre and convenient radius, draw an arc, which intersects \(\overline{P Q}\) at A and B.
(iii) Taking A and B as centres and radius more than half of AB, draw two arcs intersecting each other at R.
(iv) Join OR. Thus, ∠QOR = ∠POR = 90°.
(v) Draw \(\overline{O D}\) the bisector of ∠POR.
Thus, ∠QOD is the required angle of 135°.

Question 6.
Draw an angle of measure 45° and bisect it.
Solution:
Steps of construction :

(i) Draw a line PQ and take a point O on it.
(ii) Taking O as centre and a convenient radius, draw an arc which intersects \(\overline{P Q}\) at two points A and B.
(iii) Taking A and B as centres and radius more than half of AB, draw two arcs which intersect each other at C.
(iv) Join OC. Then ∠COQ is an angle of 90°.
(v) Draw \(\overline{O E}\) as the bisector of ∠COQ. Thus ∠QOE = 45°.
(vi) Again draw \(\overline{O G}\) as the bisector of ∠QOE.
Thus, ∠QOG = ∠EOG = \(22 \frac{1}{2}^{\circ}\).

Question 7.
Draw an angle of measure 135° and bisect it.
Solution:
Steps of construction :

(i) Draw a line \(\overline{P Q}\) and take a point O on it.
(ii) Taking O as centre and convenient radius, draw an arc, which intersects \(\overline{P Q}\) at A and B.
(iii) Taking A. and B as centres and radius more than half of AB, draw two arcs intersecting each other at R.
(iv) Join OR. Thus, ∠QOR = ∠POR = 90°.
(v) Draw \(\overline{O D}\) the bisector of ∠POR. Thus, ∠QOD is the required angle of 135°.
(vi) Now, draw \(\overline{O E}\) as the bisector of ∠QOD.
Thus, ∠QOE = ∠DOE = \(67 \frac{1}{2}^{\circ}\) .

Question 8.
Draw an angle of 70°. Make a copy of it using only a straight edge and compasses.
Solution:
Steps of construction:

(i) Draw an angle of 70° with the help of protractor, i.e., ∠POQ = 70°.
(ii) Draw \(\overline{A B}\).
(iii) Place the compasses at O and draw an arc to cut the rays of ∠POQ at L and M.
(iv) Use the same compasses setting to draw an arc with A as centre, cutting AB at X.
(v) Set your compasses setting to the length LM with the same radius.
(vi) Place the compasses pointer at X and draw the arc to cut the arc drawn earlier at Y.
(vii) Join AY.
Thus, ∠YAX = 70°.

Question 9.
Draw an angle of 40°. Copy its supplementary angle.
Solution:
Steps of construction :

(i) Draw an angle of 40° with the help of protractor, i.e., ∠AOB = 40°.
(ii) Draw a line \(\overline{P Q}\).
(iii) Take any point M on PQ.
(iv) Place the compasses at O and draw an arc to cut the rays of ∠AOB at L and N.
(v) Use the same compasses setting to draw an arc M as centre, cutting MQ at X.
(vi) Set your compasses to length LN with the same radius.
(vii) Place the compasses at X and draw the arc to cut the arc drawn earlier at Y.
(viii) Join MY.
(ix) Thus, ∠QMY = 40° and ∠PMY is supplementary of it.

MP Board Class 6th Maths Solutions

MP Board Class 6th Maths Solutions Chapter 2 Whole Numbers Ex 2.3

Question 1.
Which of the following will not represent zero:
(a) 1 + 0
(b) 0 × 0
(c) \(\frac{0}{2}\)
(d) \(\frac{10-10}{2}\)
Solution:
(a) 1 + 0 = 1
(b) 0 × 0 = 0
(c) \(\frac{0}{2}\) = 0
(d) \(\frac{10-10}{2}\) = \(\frac{0}{2}\) = 0
Thus, (a) does not represent zero.

Question 2.
If the product of two whole numbers is zero, can we say that one or both of them will be zero? Justify through examples.
Solution:
Yes, if we multiply any number with zero, then the product will be zero.
i. e., 2 × 0 = 0, 5 × 0 = 0, 9 × 0 = 0
If both numbers are zero, then the product will also be zero, i.e., 0 × 0 = 0

Question 3.
If the product of two whole numbers is 1, can we say that one or both of them will be 1? Justify through examples.
Solution:
No, if only one number be 1, then the product cannot be 1.
i.e., 5 × 1 = 5, 4 × 1 = 4, 8 × 1 = 8
If both numbers are 1, then the product is 1
i.e., 1 × 1 = 1

Question 4.
Find using distributive property:
(a) 728 × 101
(b) 5437 × 1001
(c) 824 × 25
(d) 4275 × 125
(e) 504 × 35
Solution:
(a) 728 × 101
= 728 × (100 + 1)
= 728 × 100 + 728 × 1
= 72800 + 728
= 73528

(b) 5437 × 1001
= 5437 × (1000 + 1)
= 5437 × 1000 + 5437 × 1
= 5437000 + 5437
= 5442437

(c) 824 × 25
= 824 × (20 + 5)
= 824 × 20 + 824 × 5
= 16480 + 4120
= 20600

(d) 4275 × 125
= 4275 × (100 + 20 + 5)
= 4275 × 100 + 4275 × 20 + 4275 × 5
= 427500 + 85500 + 21375
= 534375

(e) 504 × 35
= (500 + 4) × 35
= 500 × 35 + 4 × 35
= 17500 + 140
= 17640

Question 5.
Study the pattern :
1 × 8 + 1 = 9
12 × 8 + 2 = 98
123 × 8 + 3 = 987
1234 × 8 + 4 = 9876
12345 × 8 + 5 = 98765
Write the next two steps. Can you say how the pattern works?
(Hint: 12345 = 11111 + 1111 + 111 + 11 + 1).
Solution:
The next two steps are :
123456 × 8 + 6 = 987654
1234567 × 8 + 7 = 9876543
Pattern works like this :
1 × 8 + 1 = 9
12 × 8 + 2 = 98
123 × 8 + 3 = 987
1234 × 8 + 4 = 9876
12345 × 8 + 5 = 98765
123456 × 8 + 6 = 987654
1234567 × 8 + 7 = 9876543

MP Board Class 6th Maths Solutions

MP Board Class 6th Maths Solutions Chapter 2 Whole Numbers Ex 2.2

Question 1.
Find the sum by suitable rearrangement:
(a) 837 + 208 + 363
(b) 1962 + 453 + 1538 + 647
Solution:
(a) 837 + 208 + 363
= (837 + 363) + 208
= 1200 + 208 = 1408

(b) 1962 + 453 + 1538 + 647
= (1962 + 1538) + (453 + 647)
= 3500 + 1100 = 4600

Question 2.
Find the product by suitable rearrangement:
(a) 2 × 1768 × 50
(b) 4 × 166 × 25
(c) 8 × 291 × 125
(d) 625 × 279 × 16
(e) 285 × 5 × 60
(f) 125 × 40 × 8 × 25
Solution:
(a) 2 × 1768 × 50
= (2 × 50) × 1768 – 100 × 1768
= 176800

(b) 4 × 166 × 25
= (4 × 25) × 166
= 100 × 166
= 16600

(c) 8 × 291 × 125
= (8 × 125) × 291
= 1000 × 291
= 291000

(d) 625 × 279 × 16
= (625 × 16) × 279
= 10000 × 279
= 2790000

(e) 285 × 5 × 60
= 285 × (5 × 60)
= 285 × 300
= 85500

(f) 125 × 40 × 8 × 25
= (125 × 8) × (40 × 25)
= 1000 × 1000
= 1000000

Question 3.
Find the value of the following:
(a) 297 × 17 + 297 × 3
(b) 54279 × 92 + 8 × 54279
(c) 81265 × 169 – 81265 × 69
(d) 3845 × 5 × 782 + 769 × 25 × 218
Solution:
(a) 297 × 17 + 297 × 3
= 297 × (17 + 3)
= 297 × 20
= 5940

(b) 54279 × 92 + 8 × 54279
= 54279 × (92 + 8)
= 54279 × 100
= 5427900

(c) 81265 × 169 – 81265 × 69
= 81265 × (169 – 69)
= 81265 × 100
= 8126500

(d) 3845 × 5 × 782 + 769 × 25 × 218
= 3845 × 5 × 782 + 769 × 5 × 5 × 218
= 3845 × 5 × 782 + 3845 × 5 × 218
= 3845 × 5 × (782 + 218)
= 19225 × 1000
= 19225000

Question 4.
Find the product using suitable properties.
(a) 738 × 103
(b) 854 × 102
(c) 258 × 1008
(d) 1005 × 168
Solution:
By using distributive property of multiplication over addition, we get
(a) 738 × 103
= 738 × (100 + 3)
= 738 × 100 + 738 × 3
= 73800 + 2214 = 76014

(b) 854 × 102
= 854 × (100 + 2)
= 854 × 100 + 854 × 2
= 85400 + 1708
= 87108

(c) 258 × 1008
= 258 × (1000+ 8)
= 258 × 1000 + 258 × 8
= 258000 + 2064
= 260064

(d) 1005 × 168
= (1000 + 5) × 168
= 1000 × 168 + 5 × 168
= 168000 + 840
= 168840

Question 5.
A taxidriver filled his car petrol tank with 40 litres of petrol on Monday. The next day, he filled the tank with 50 litres of petrol. If the petrol costs ₹ 44 per litre, how much did he spend in all on petrol?
Solution:
Petrol filled on Monday = 40 litres Petrol filled on next day = 50 litres
Total petrol filled = (40 + 50) litres = 90 litres
Now, cost of 1 litre of petrol = ₹ 44
Cost of 90 litres of petrol = ₹ (44 × 90)
= ₹ 3960
Therefore, the taxidriver spent ₹ 3960 on petrol.

Question 6.
A vendor supplies 32 litres of milk to a hotel in the morning and 68 litres of milk in the evening. If the milk costs ₹ 15 per litre, how much money is due to the vendor per day?
Solution:
Supply of milk in the morning = 32 litres
Supply of milk in the evening = 68 litres
Total supply of milk = (32 + 68) litres
= 100 litres
Now, cost of 1 litre milk = ₹ 15
Cost of 100 litres milk = ₹ (15 × 100)
= ₹ 1500
Therefore, ₹ 1500 is due to the vendor per day.

Question 7.

Solution:
(i) 425 × 136 = 425 × (6 + 30 + 100)
This is the principle of distributivity of multiplication over addition.

(ii) 2 × 49 × 50 = 2 × 50 × 49
This is the principle of commutativity under multiplication.

(iii) 80 + 2005 + 20 = 80 + 20 + 2005
This is the principle of commutativity under addition.

MP Board Class 6th Maths Solutions

MP Board Class 6th Maths Solutions Chapter 14 Practical Geometry Ex 14.5

Question 1.
Draw \(\overline{A B}\) of length 7.3 cm and find its axis of symmetry.
Solution:
Axis of symmetry of line segment \(\overline{A B}\) will be the perpendicular bisector of \(\overline{A B}\). So, draw the perpendicular bisector of AB.
Steps of construction:

(i) Draw \(\overline{A B}\) = 7.3 cm.
(ii) With A as centre and radius more than half of AB, draw two arcs, one on each side of AB.
(iii) With B as a centre and the same radius as in step (ii), draw arcs cutting the arcs drawn in the previous step at C and D.
(iv) Join CD. Then CD is the axis of symmetry of the line segment AB.

Question 2.
Draw a line segment of length 9.5 cm and construct its perpendicular bisector.
Solution:
Steps of construction :

(i) Draw \(\overline{A B}\) = 9.5 cm.
(ii) With A as centre and radius more than half of AB, draw two arcs one on each side of AB.
(iii) With B as a centre and the same radius as in step (ii), draw arcs cutting the arcs drawn in the previous step at C and D.
(iv) Join CD. Then CD is the perpendicular bisector of \(\overline{A B}\).

Question 3.
Draw the perpendicular bisector of \(\overline{X Y}\) whose length is 10.3 cm.
(a) Take any point P on the bisector drawn. Examine whether PX = PY.
(b) If M is the mid point of \(\overline{X Y}\), what can you say about the lengths MX and XY?
Solution:
Steps of construction :

(i) Draw \(\overline{X Y}\) = 10.3 cm.
(ii) With X as centre and radius more than half of XY, draw two arcs one on each side of XY.
(iii) With Y as centre and the same radius as in step (ii), draw two arcs cutting the arcs drawn in the previous step at C and D.
(iv) Join CD. Then CD is the required perpendicular bisector of \(\overline{X Y}\).
Now
(a) Take any point P on the bisector drawn. With the help of divider we can check that \(\overline{P X}=\overline{P Y}\) if P is the point of intersection of XY and CD.
(b) If M is the mid-point of \(\overline{X Y}\), then \(\overline{M X}=\frac{1}{2} \overline{X Y}\)

Question 4.
Draw a line segment of length 12.8 cm. Using compasses, divide it into four equal parts. Verify by actual measurement.
Solution:
Steps of construction:

(i) Draw AB = 12.8 cm.
(ii) Draw the perpendicular bisector of \(\overline{A B}\) which cuts it at C. Thus, C is the mid-point of \(\overline{A B}\).
(iii) Draw the perpendicular bisector of \(\overline{A C}\) which cuts it at D. Thus D is the mid-point of AC.
(iv) Again, draw the perpendicular bisector of \(\overline{C B}\) which cuts it at E. Thus, E is the mid-point of \(\overline{C B}\).
(v) Now, point C, D and E divide \(\overline{A B}\) in four equal parts.
(vi) By actual measurement, we find that \(\overline{A D}=\overline{D C}=\overline{C E}=\overline{E B}\) = 3.2 cm

Question 5.
With \(\overline{P Q}\) of length 6.1 cm as diameter, draw a circle.
Solution:
Steps of construction :

(i) Draw a line segment \(\overline{P Q}\) = 6.1 cm.
(ii) Draw the perpendicular bisector of PQ which cuts, it at O. Thus O is the mid-point of \(\overline{P Q}\).
(iii) Taking O as centre and OP or OQ as radius draw a circle where \(\overline{P Q}\) is the diameter.

Question 6.
Draw a circle with centre C and radius 3.4 cm. Draw any chord \(\overline{A B}\). Construct the perpendicular bisector of \(\overline{A B}\) and examine if it passes through C.
Solution:
Steps of construction:

(i) Draw a circle with centre C and radius 3.4 cm.
(ii) Draw any chord \(\overline{A B}\).
(iii) With A as center and radius more than half of \(\overline{A B}\), draw two arcs one on each side of AB.
(iv) With B as a centre and the radius same as in step (iii), draw two arcs cutting the arcs drawn in the previous step at P and Q.
(v) Join PQ. Then PQ is the perpendicular bisector of \(\overline{A B}\).
(vi) This perpendicular bisector of \(\overline{A B}\) passes through the centre C of the circle.

Question 7.
Repeat Question 6, if \(\overline{A B}\) happens to be a diameter.
Solution:
Steps of construction :

(i) Draw a circle with centre C and radius 3.4 cm.
(ii) Draw its diameter AB.
(iii) With A as center and radius more than half of AB, draw two arcs one on each side of AB.
(iv) With B as a centre and the radius same as in step (iii), draw two arcs cutting the arcs drawn in the previous step at P and Q.
(v) Join PQ. Then PQ is the perpendicular bisector of \(\overline{A B}\).
(vi) We observe that this perpendicular bisector of \(\overline{A B}\) intersect it at the centre C of the circle.

Question 8.
Draw a circle of radius 4 cm. Draw any two of its chords. Construct the perpendicular bisectors of these chords. Where do they meet?
Solution:
Steps of construction :

(i) Draw the circle with centre O and radius 4 cm.
(ii) Draw any two chords AB and CD in this, circle.
(iii) With A as center and radius more than half AB, draw two arcs one on each side of AB.
(iv) With B as centre and radius same as in step (ii), draw two arcs cutting the arcs drawn in previous step at E and F.
(v) Join EF. Thus EF is the perpendicular bisector of chord AB.
(vi) Similarly, draw GH the perpendicular bisector of chord CD.
(vii) These two perpendicular bisectors meet at O, the centre of the circle.

Question 9.
Draw any angle with vertex O. Take a point A on one’ of its arms and B on another such that OA = OB. Draw the perpendicular bisectors of \(\overline{O A}\) and \(\overline{O B}\). Let them meet at P. Is PA = PB?
Solution:
Steps of construction :

(i) Draw any angle with vertex O.
(ii) Take a point A on one of its arms and B on another such that OA = OB.
(iii) Draw perpendicular bisector of OA and OB.
(iv) Let they meet at P. Join PA and PB.
(v) With the help of divider, we check that PA = PB.

MP Board Class 6th Maths Solutions