Bhagya

In this article, we will share MP Board Class 10th Maths Book Solutions Chapter 7 Coordinate Geometry Ex 7.1 Pdf, These solutions are solved subject experts from the latest edition books.

MP Board Class 10th Maths Solutions Chapter 7 Coordinate Geometry Ex 7.1

Question 1.
Find the distance between the following pairs of points:
(i) (2, 3), (4, 1)
(ii) (-5, 7), (-1, 3)
(iii) (a, b), (-a, -b)
Solution:
(i) Here x₁ = 2, y₁ = 3 and x₂ = 4, y₂ = 1
∴ The required distance

(ii) Here x₁ = -5, y₁ = 7 and x₂ = -1, y₂ = 3
∴ The required distance

(iii) Here x₁ = a, y₁ = b and x₂ = -a, y₂ = -b
∴ The required distance

Question 2.
Find the distance between the points (0, 0) and (36, 15). Can you now find the distance between the two towns /I and B discussed below as following: ‘A town 6 is located 36 km east and 15 km north of the town A’.
Solution:
Part-I
Let the points be A(0, 0) and B(36, 15)

Part-II
We have A(0, 0) and B(36,15) as the positions of two towns.

Question 3.
Determine if the points (1, 5), (2, 3) and (-2, -11) are collinear.
Solution:
Let the points be A( 1, 5), B(2, 3) and C(-2, -11). A, B and C are collinear, if
AB + BC = AC or AC + CB = AB or BA + AC = BC

Here, AB + BC ≠ AC, AC + CB ≠ AB, BA + AC ≠ BC
∴ A, B and C are not collinear.

Question 4.
Check whether (5, -2), (6, 4) and (7, -2) are the vertices of an isosceles triangle.
Solution:
Let the points be A(5, -2), 6(6, 4) and C(7, -2).

We have AB = BC ≠ AC.
∴ ∆ABC is an isosceles triangle.

Question 5.
In a classroom, 4 friends are seated at the points A B, Cand D as shown in the figure. Champa and Chameli walk into the class and after observing for a few minutes Champa asks Chameli, “Don’t you think ABCD is a square?” Chameli disagrees. Using distance formula, find which of them is correct.

Solution:
Let the horizontal columns represent the x-coordinates whereas the vertical rows represent the y-coordinates.
∴ The points are A(3, 4), B(6, 7), C(9, 4) and D(6, 1)


i.e., BD = AC ⇒ Both the diagonals are also equal.
∴ ABCD is a square.
Thus, Champa is correct.

Question 6.
Name the type of quadrilateral formed if any, by the following points, and give reasons for your answer:
(i) (-1, -2), (1, 0), (-1, 2), (-3, 0)
(ii) (-3, 5), (3, 1), (0, 3), (-1, -4)
(iii) (4, 5), (7, 6), (4, 3), (1, 2)
Solution:
(i) Let the points be A(-1, -2), B(1, 0), C(-1, 2) and D(-3, 0) of a quadrilateral ABCD.

⇒ AB = BC = CD = AD i.e., all the sides are equal.
Also, AC and BD (the diagonals) are equal.
∴ ABCD is a square.

(ii) Let the points be A(-3, 5), B(3, 1), C(0, 3) and D(-1, -4).


We see that \(\sqrt{13}+\sqrt{13}=2 \sqrt{13}\)
i. e., AC + BC = AB
⇒ A, B and C are collinear. Thus, ABCD is not a quadrilateral.

(iii) Let the points be A(4, 5), B(7, 6), C(4, 3) and D(1, 2).

Since, AB = CD, BC = DA i.e., opposite sides of the quadrilateral are equal.
And AC ≠ BD ⇒ Diagonals are unequal.
∴ ABCD is a parallelogram.

Question 7.
Find the point on x-axis which is equidistant from (2, -5) and (-2, 9).
Solution:
We know that any point on x-axis has its ordinate = 0
Let the required point be P(x, 0)
Let the given points be A(2, -5) and B(-2, 9)


∴ The required point is (-7, 0)

Question 8.
Find the values of y for which the distance between the points P(2, -3) and Q(10, y) is 10 units.
Solution:
The given points are P(2, -3) and Q(10, y).

Squaring both sides, y² + 6y + 73 = 100
⇒ y² + 6y – 27 = 0
⇒ y² – 3y + 9y – 27 = 0
⇒ (y – 3)(y + 9) = 0
Either y – 3 = 0 ⇒ y = 3
or y + 9 = 0 ⇒ y = -9
∴ The required value of y is 3 or -9.

Question 9.
If Q(0, 1) is equidistant from P(5, -3) and R(x, 6), find the values of x. Also find the distances QR and PR.
Solution:

Squaring both sides, we have x² + 25 = 41
⇒ x² + 25 – 41 = 0
⇒ x² – 16 = 0 ² x = \(\pm \sqrt{16}\) = ±4
Thus, the point R is (4, 6) or (-4, 6)
Now,

Question 10.
Find a relation between x and y such that the point (x, y) is equidistant from the point (3, 6) and (-3, 4).
Solution:
Let the points be A(x, y), B(3, 6) and C(-3, 4).
∴ AB = \(\sqrt{(3-x)^{2}+(6-y)^{2}}\)
And AC = \(\sqrt{[(-3)-x]^{2}+(4-y)^{2}}\)
Since, the point (x, y) is equidistant from (3, 6) and (-3, 4).
∴ AB = AC
⇒ \(\sqrt{(3-x)^{2}+(6-y)^{2}}=\sqrt{(-3-x)^{2}+(4-y)^{2}}\)
Squaring both sides,
(3 – x)² + (6 – y)² = (-3 – x)² + (4 – y)²
⇒ (9 + x² – 6x) + (36 + y² – 12y)
⇒ (9 + x² + 6x) + (16 + y² – 8y)
⇒ 9 + x² – 6x + 36 + y² – 12y – 9 – x² – 6x – 16 – y² + 8y = 0
⇒ – 6x – 6x + 36 – 12y – 16 + 8y = 0
⇒ – 12x – 4y + 20 = 0
⇒ -3x – y + 5 = 0
⇒ 3x + y – 5 = 0 which is the required relation between x and y.

In this article, we will share MP Board Class 10th Maths Book Solutions Pair of Linear Equations in Two Variables Ex 3.2 Pdf, These solutions are solved subject experts from the latest edition books.

MP Board Class 10th Maths Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.2

Question 1.
Form the pair of linear equations in the following problems, and find their solutions graphically.
(i) 10 students of class X took part in a Mathematics quiz. If the number of girls is 4 more than the number of boys, find the number of boys and girls who took part in the quiz.
(ii) 5 pencils and 7 pens together cost ₹ 50, whereas 7 pencils and 5 pens together cost ₹ 46. Find the cost of one pencil and that of one pen.
Solution:
(i) Let the number of boys = x and Number of girls = y
∴ x + y = 10 …. (1)
Also, Number of girls = [Number of boys] + 4
∴ y = x + 4 ⇒ x – y = – 4 … (2)
Now, from the equation (1), we have :
l₁ : x + y = 10 ⇒ y = 10 – x

And from the equation (2), we have
l₂ : x – y = -4 ⇒ y = x + 4

The lines l₁ and l₂ intersects at the point (3, 7)
∴ The solution of the pair of linear equations is : x = 3, y = 7
⇒ Number of boys = 3
and number of girls = 7
Let the cost of a pencil = ₹ x
and cost of a pen = ₹ y
Since, cost of 5 pencils + Cost of 7 pens = ₹ 50
5 x + 7y = 50 … (1)
Also, cost of 7 pencils + cost of 5 pens = ₹ 46
7x + 5y = 46 …. (2)
Now, from equation (1), we have

And from equation (2), we have

Plotting the points (10, 0), (3, 5) and (-4, 10), we get a straight line l₁ and plotting the points (8, -2), (3, 5) and (0, 9.2) we get a straight line l₂.

These two straight lines intersects at (3, 5).
∴ Cost of a pencil = ₹ 3 and cost of a pen = ₹ 5.

Question 2.
On comparing the ratios \(\frac{a_{1}}{a_{2}}, \frac{b_{1}}{b_{2}}\) and \(\frac{c_{1}}{c_{2}}\) find out whether the lines representing the following pairs of linear equations intersect at a point, are parallel or coincident:
(i) 5x – 4y + 8 = 0; 7x + 6y – 9 = 0
(ii) 9x + 3y + 12 = 0; 18x + 6y + 24 = 0
(iii) 6x – 3y + 10 = 0; 2x – y + 9 = 0
Solution:
Comparing the given equations with
a₁x + b₁y + C₁ = 0, a₂x + b₂y + c₂ = 0, we have

(i) For, 5x – 4y + 8 = 0, 7x + 6y – 9 = 0,
a₁ = 5, b₁ = -4, C₁ = 8; a₂ = 7, b₂ = 6, c₂ = -9

So, the lines are intersecting, i.e., they intersect at a point.

(ii) For, 9x + 3y + 12 = 0,18x + 6y + 24 = 0,
a₁ = 9, b₁ = 3, C₁ = 12; a₂ = 18, b₂ = 6, c₂ = 24

So, the lines are coincident.

(iii) For, 6x – 3y +10 = 0, 2x – y + 9 = 0

So, the lines are parallel.

Question 3.
On comparing the ratios \(\frac{a_{1}}{a_{2}}, \frac{b_{1}}{b_{2}}\) and \(\frac{c_{1}}{c_{2}}\), find out whether the following pair of linear equations are consistent, or inconsistent.
(i) 3x + 2y = 5; 2x – 3y = 7
(ii) 2x – 3y = 8; 4x – 6y = 9
(iii) \(\frac{3}{2} x+\frac{5}{3} y\) = 7; 9x-10y = 14
(iv) 5x – 3y = 11; -10x + 6y = -22
Solution:
Comparing the given equations with

So, lines are intersecting i.e., they intersect at a point.
∴ It is consistent pair of equations.

(ii) For 2x – 3y = 8, 4x – 6y = 9, 2x – 3y – 8 = 0 and 4x – 6y – 9 = 0

So, lines are parallel i.e., the given pair of linear equations has no solution.
∴ It is inconsistent pair of equations.

(iii)

⇒ The given pair of linear equations has exactly one solution.
∴ It is a consistent pair of equations.

(iv)

So, lines are coincident.
⇒ The given pair of linear equations has infinitely many solutions.
Thus, it is consistent pair of equations

(v)

So, the lines are coincident.
⇒ The given pair of linear equations have infinitely many solutions.
Thus it is consistent pair of equations.

Question 4.
Which of the following pairs of linear equations are consistent / inconsistent? If consistent, obtain the solution graphically:
(i) x + y = 5; 2x + 2y = 10
(ii) x – y = 8; 3x – 3y = 16
(iii) 2x + y – 6 = 0; 4x – 2y – 4 = 0
(iv) 2x – 2y – 2 = 0; 4x – 4y – 5 = 0
Solution:
(i) For, x + y = 5, 2x + 2y = 10 ⇒ x + y – 5 = 0 and 2x + 2y – 10 = 0


So, lines l₁ and l₂ are coinciding. i.e., They have infinitely many solutions.

(ii) For, x – y = 8,
3x – 3y = 16
⇒ x – y – 8 = 0
and 3x – 3y = 16

so, line are parallel
∴ The pair of linear equations are inconsistent

(iii) For 2x + y – 6 = 0, 4x – 2y – 4 = 0


The pair of linear equations are inconsistent

Question 5.
Half the perimeter of a rectangular garden, whose length is 4 m more than its width, is 36 m. Find the dimensions of the garden.
Solution:
Let the width of the garden = x m
and the length of the garden = y m
According to question,


The lines l₁ and l₂ intersect at (16, 20).
∴ x = 16 and y = 20
So, Length = 20m, and Width = 16m

Question 6.
Given the linear equation 2x + 3y – 8 = 0, write another linear equation in two variables such that the geometrical representation of the pair so formed is:
(i) intersecting lines
(ii) parallel lines
(iii) coincident lines
Solution:
Let the pair of linear equations be 2x + 3y – 8 = 0
⇒ a₁ = 2, b₁ = 3 and C₁ = -8 and a₂x + b₂y + c₂ = 0.

(i) For intersecting lines, we have:

∴ We can have a₂ = 3, b₂ = 2 and c₂ = – 7
∴ The required equation can be 3x + 2y – 7 = 0

(ii) For parallel lines, \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}\)
∴ Any line parallel to 2x + 3y – 8 = 0, can be taken as 2x + 3y -12 = 0

(iii) For coincident lines, \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}\)
∴ Any line parallel to 2x + 3y – 8 = 0 can be 2(2x + 3y – 8 = 0)
⇒ 4x + 6y – 16 = 0

Question 7.
Draw the graphs of the equations x – y + 1 = 0 and 3x + 2y – 12 = 0. Determine the coordinates of the vertices of the triangle formed by these lines and the x-axis, and shade the triangular region.
Solution:
Since, we have

The lines l₁ and l₂ intersect at (2, 3). Thus, co-ordinates of the vertices of the shaded triangular region are (4, 0), (-1, 0) and (2, 3).

In this article, we will share MP Board Class 10th Maths Book Solutions Pair of Linear Equations in Two Variables Ex 3.4 Pdf, These solutions are solved subject experts from the latest edition books.

MP Board Class 10th Maths Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.4

Question 1.
Solve the following pair of linear equations by the elimination method and the substitution method:
(i) x + y = 5 and 2x – 3y = 4
(ii) 3x + 4y = 10 and 2x – 2y = 2
(iii) 3x – 5y – 4 = 0 and 9x = 2y + 7
(iv) \(\frac{x}{2}+\frac{2 y}{3}\) = -1 and \(x-\frac{y}{3}\) = 3
Solution:
(i) Elimination method :
x + y = 5 … (1)
2x – 3y = 4 …. (2)
Multiplying (1) by 3, we get
3x + 3y = 15 …. (3)
Adding (2) and (3) , we get
2x – 3y + 3x + 3y = 19
⇒ 5x = 19 ⇒ x = \(\frac{19}{5}\)
Now, putting x = \(\frac{19}{5}\) in (1) , we get

Substitution Method :
x + y = 5 ⇒ y = 5 – x … (1)
2x – 3y = 4 … (2)
Put y = 5 – x in (2), we get
2x – 3(5 – x)= 4 ⇒ 2x – 15 + 3x = 4

(ii) Elimination method :
3x + 4y = 10 … (1)
2x – 2y = 2 … (2)
Multiplying equation (2) by 2, we have
⇒ 4x – 4y = 4 … (3)
Adding (1)and (3) , we get
3x + 4y + 4x – 4y = 10 + 4
⇒ 7x = 14 ⇒x = \(\frac{14}{7}\) = 2
Putting x = 2 in (1) , we get,
3(2)+ 4y = 10

(iii) Elimination method :
3x – 5y – 4 = 0 … (1)
9x = 2y + 7 ⇒ 9x – 2y – 7 = 0 …. (2)
Multiplying equation (1) by (3) , we get
⇒ 9x – 15y – 12 = 0(3)
Subtracting (2)from (3),
⇒ 9x – 15y – 12 – 9x + 2y + 7 = 0

(iv) Elimination method :

Question 2.
Form the pair of linear equations in the following problems and find their solutions (if they exist) by the elimination method:
(i) If we add 1 to the numerator and subtract 1 from the denominator, a fraction reduces 1
to 1. It becomes \(\frac{1}{2}\) if we only add 1 to the denominator. What is the fraction?
(ii) Five years ago, Nuri was thrice as old as Sonu. Ten years later, Nuri will be twice as old as Sonu. How old are Nuri and Sonu?
(iii) The sum of the digits of a two-digit number is 9. Also, nine times this number is twice the number obtained by reversing the order of the digits. Find the number.
(iv) Meena went to a bank to withdraw ₹ 2000. She asked the cashier to give her ₹ 50 and ₹ 100 notes only. Meena got 25 notes in all. Find how many notes of ₹ 50 and ₹ 100 she received.
(v) A lending library has a fixed charge for the first three days and an additional charge for each day thereafter. Saritha paid ₹ 27 for a book kept for seven days, while Susy paid ₹ 21 for the book she kept for five days. Find the fixed charge and the charge for each extra day.
Solution:
(i)Let the numerator = x
and the denominator = y

(ii) Let, present age of Nuri = x years
and the present age of Sonu = y years
Age of Nuri = (x – 5) years
Age of Sonu = (y – 5) years
According to question:
Age of Nuri = 3[Age of sonu]
⇒ x – 5 = 3[y – 5] ⇒ x – 5 = 3y – 15
⇒ x – 3y + 10 = 0 … (1)
10 years later :
Age of Nuri = (x + 10) years,
Age of Sonu = (y + 10) years,
According to question :
Age of Nuri = 2[Age of Sonu]
⇒ x + 10 = 2(y + 10) ⇒ x + 10 = 2y + 20
⇒ x – 2y -10 = 0 …. (2)
Subtracting (1) from (2),
x – 2y – 10 – x + 3y – 10 = 0 ⇒ y – 20 = 0 ⇒ y = 20
Putting y = 20 in (1), we get
x – 3(20) + 10 = 0 ⇒ x – 50 = 0 ⇒ x = 50
Thus, x = 50 and y = 20
∴ Age of Nuri = 50 years
and age of Sonu = 20 years

(iii) Let the digit at unit’s place = x
and the digit at ten’s place = y
∴ The number = 10y + x
The number obtained by reversing the digits = 10x + y
According to question,
9[The number] = 2 [Number obtained by reversing the digits]
9[10y+ x] = 2[10x + y]
90y + 9x = 20x + 2y
x – 8y = 0 …. (1)
Also sum of the digits = 9
x + y = 9 …. (2)
Subtracting (1) from (2), we have
x + y – x + 8y = 9
⇒ 9y = 9 ⇒ y = 1
putting y = 1 in (2), we get
x + 1 = 9 ⇒ x = 8
Thus, x = 8 and y = 1
∴ The required number = 10y + x = (10 × 1) + 8 = 10 + 8 = 18

(iv) Let the number of 50 rupees notes = x
and the number of 100 rupees notes = y
According to the condition,
Total number of notes = 25
∴ x + y = 25 …. (1)
Also, the value of all the notes = ₹ 2000
∴ 50x + 100y = 2000 ⇒ x + 2y = 40 …. (2)
Subtracting equation (1) from (2), we get
x + 2y – x – y = 40 – 25
⇒ y = 15
Putting y = 15 in (1),
x + 15 = 25
⇒ x = 25 – 15 = 10
Thus, x = 10 and y = 15
∴ Number of 50 rupees notes = 10
and number of 100 rupees notes = 15

(v) Let the fixed charge (for the three days) = ₹ x
and the additional charge for each extra day = ₹ y
According to question,
Charge for 7 days = ₹ 27
⇒ x + 4y = 27
[∵ Extra days = 7 – 3 = 4]
Also, charge of 5 days = ₹ 21
⇒ x + 2y = 21
[∵ Extra days = 5 – 3 = 2]
Subtracting (2) from (1), we get
x + 4y – x – 2y = 27 – 21
\(\Rightarrow \quad 2 y=6 \Rightarrow y=\frac{6}{2}=3\)
Putting y = 3 in (2), we have
x + 2(3) = 21
⇒ x = 21 – 6 = 15
So, x = 15 and y = 3
∴ Fixed charge = ₹ 15
and additional charge per day = ₹ 3

In this article, we will share MP Board Class 10th Maths Book Solutions Chapter 2 Polynomials Ex 2.3 Pdf, These solutions are solved subject experts from the latest edition books.

MP Board Class 10th Maths Solutions Chapter 2 Polynomials Ex 2.3

Question 1.
Divide the polynomial p(x) by the polynomial g(x) and find the quotient and remainder in each of the following:
(i) p(x) = x³ – 3x² + 5x – 3, g(x) = x² – 2
(ii) p(x) = x⁴ – 3x² + 4x + 5, g(x) = x² + 1 – x
(iii) p(x) = x⁴ – 5x + 6, g(x) = 2 – x²
Solution:
(i) Here, dividend p(x) = x³ – 3x² + 5x – 3, and divisor g(x) = x² – 2
∴ We have

Thus, the quotient = (x – 3) and remainder = (7x – 9)

(ii) Here, dividend p(x) = x⁴ – 3x² + 4x + 5 and divisor g(x) = x² + 1 – x = x² – x + 1
∴ We have

Thus, the quotient = (x² + x – 3) and remainder = 8

(iii) Here, dividend, p(x) = x⁴ – 5x + 6 and divisor, g(x) = 2 – x² = – x² + 2
∴ We have

Thus, the quotient = -x² – 2 and remainder = -5x +10

Question 2.
Check whether the first polynomial is a factor of the second polynomial by dividing the second polynomial by the first polynomial:
(i) t² – 3; 2t⁴ + 3t³ -2t² – 9t – 12
(ii) x² + 3x + 1; 3x⁴ + 5x³ – 7x² + 2x +2
(iii) x³ – 3x + 1; x⁵ – 4x³ + x² + 3x + 1
Solution:
(i) Dividing 2t⁴ + 3t³ – 2t² – 9t – 12 by t² – 3, we have

∵ Remainder = 0
∴ (t² – 3) is a factor of 2t⁴ + 3t³ – 2t² – 9t – 12.

(ii) Dividing 3x⁴ + 5x³ – 7x² + 2x + 2 by x² + 3x + 1, we have

∵ Remainder = 0
∴ x² + 3x + 1 is a factor of 3x⁴ + 5x³ – 7x² + 2x + 2.

(iii) Dividing x⁵ – 4x³ + x² + 3x + 1 by x³ – 3x + 1, we get

∵ Remainder = 2, i.e., remainder = 0
∴ x³ – 3x + 1 is not a factor of x⁵ – 4x³ + x² + 3x +1.

Question 3.
Obtain all other zeroes of 3x⁴ + 6x³ – 2x² – 10x – 5, if two of its zeroes are \(\sqrt{\frac{5}{3}}\) and \(-\sqrt{\frac{5}{3}}\)
Solution:
We have p(x) = 3x⁴ + 6x³ – 2x² – 10x – 5.
Given \(\sqrt{\frac{5}{3}}\) and \(-\sqrt{\frac{5}{3}}\) are zeroes of p(x).

Thus, the other zeroes of the given polynomial are -1 and -1.

Question 4.
On dividing x³ – 3x² + x + 2 by a polynomial g(x), the quotient and remainder were x – 2 and -2x + 4, respectively. Find g(x).
Solution:
Here, dividend, p(x) = x³ – 3x² + x + 2, divisor = g(x), quotient = (x – 2) and remainder = (-2x + 4)
Since, (Quotient × Divisor) + Remainder = Dividend
∴ [(x – 2) × g(x)] + [(-2x + 4)] = x³ – 3x² + x + 2
⇒ (x – 2) × g(x)
= x³ – 3x² + x + 2 – (-2x + 4)
= x³ – 3x² + x + 2 + 2x – 4
= x³ – 3x² + 3x – 2
= x³ – 3x² + 3x – 2

Thus, the required divisor g(x) = x² – x + 1

Question 5.
Give examples of polynomials p(x), g(x), q(x) and r(x), which satisfy the division algorithm and
(i) deg p(x) = deg q(x)
(ii) deg q(x) = deg r(x)
(iii) deg r(x) = 0
Solution:
(i) p(x) = 3x² – 6x + 27,
g(x) = 3 and q(x) = x² – 2x + 9.
Now, deg p(x) = deg q(x)
r(x) = 0
⇒ p(x) = q(x) × g(x) + r(x)

(ii) p(x) = 2x³ – 2x² + 2x + 3,
g(x) = 2x² – 1, and
r(x) = 3x + 2, deg q(x) = deg r(x)
⇒ p(x) = q(x) × g(x) + r(x)

(iii) p(x) = 2x³ – 4x² + x + 4,
g(x) = 2x² + 1,
q(x) = x – 2 and r(x) = 6,
deg r(x) = 0
⇒ p(x) = q(x) × g(x) + r(x)

In this article, we will share MP Board Class 10th Maths Book Solutions Chapter 2 Polynomials Ex 2.4 Pdf, These solutions are solved subject experts from the latest edition books.

MP Board Class 10th Maths Solutions Chapter 2 Polynomials Ex 2.4

Question 1.
Verify that the numbers given alongside of the cubic polynomials below are their zeroes. Also verify the relationship between the zeroes and the coefficients in each case:
(i) 2x³ + x² – 5x + 2; \(\frac{1}{2}\), 1, -2
(ii) x³ – 4x² + 5x – 2; 2, 1, 1
Solution:

Again, p(1) = 2(1)³ + (1)² – 5(1) + 2
= 2 + 1 – 5 + 2 = 0
⇒ 1 is a zero of p(x).
Also, p(-2) = 2(-2)³ + (-2)² – 5(-2) + 2
= -16 + 4 + 10 + 2 = -16 +16 = 0
= -2 is a zero of p(x).
Now, p(x) = 2x³ + x² – 5x + 2
∴ Comparing it with ax³ + bx² + cx + d, we have a = 2, b = 1, c = -5, and d = 2

Thus, the relationship between the coefficients and the zeroes of p(x) is verified.

(ii) Here, p(x) = x³ – 4x² + 5x – 2
∴ p(2) = (2)³ – 4(2)² + 5(2) – 2
= 8 – 16 + 10 – 2 = 18 – 18 = 0
⇒ 2 is a zero of p(x)
Again p(1) = (1)³ – 4(1)² + 5(1) – 2
= 1 – 4 + 5 – 2 = 6 – 6 = 0
⇒ 1 is a zero of p(x)
Now, comparing p(x) = x³ – 4x² + 5x – 2
with ax³ + bx² + cx + d = 0, we have
a = 1, b = -4, c = 5 and d = -2
Also 2, 1 and 1 are the zeroes of p(x).
Let α = 2,
β = 1,
γ = 1
Now, sum of zeroes = α + β + γ
= 2 + 1 + 1 = 4 = -b/a

Thus, the relationship between the zeroes and the coefficients of p(x) is verified.

Question 2.
Find a cubic polynomial with the sum, sum of the product of its zeroes taken two at a time, and the product of its zeroes as 2, -7, -14 respectively.
Solution:
Let the required cubic polynomial be ax³ + 6x² + cx + d = 0 and its zeroes be α, β and γ.

∴ The requied cubic polynomial is
1x³ + (-2)x² + (-7)x + 14 = 0
= x³ – 2x² – 7x + 14 = 0

Question 3.
If the zeroes of the polynomial x³ – 3x² + x + 1 are a -b, a, a + b, find a and b.
Solution:
We have p(x) = x³ – 3x² + x + 1
Comparing it with Ax³ + Bx² + Cx + D,
We have A = 1, B = -3, C = 1 and D = 1
∵ It is given (a – b), a and (a + b) are the zeroes of the polynomial.

Question 4.
If two zeroes of the polynomial
x⁴ – 6x³ – 26x²+ 138x – 35 are 2±\(\sqrt{3}\), find other zeroes.
Solution:
Here, p(x) = x⁴ – 6x³ – 26x³ + 138x – 35
∵ Two of the zeroes of p(x) are : 2 ± \(\sqrt{3}\)

(x² – 4x + 1)(x² – 2x – 35) = p(x)
⇒ (x² – 4x + 1) (x² – 7x + 5x – 35) = p(x)
⇒ (x² – 4x + 1) [x(x – 7) + 5(x – 7)] = p(x)
⇒ (x² – 4x + 1)(x – 7)(x + 5) = p(x)
i.e., (x – 7) and (x + 5) are other factors of p(x).
∴ 7 and – 5 are other zeroes of the given polynomial.

Question 5.
If the polynomial x⁴ – 6x³ + 16x² – 25x + 10 is divided by another polynomial x² – 2x + k, the remainder comes out to be x + a, find k and a.
Solution:
Applying the division algorithm to the polynomials x⁴ – 6x³ + 16x² – 25x + 10 and x² – 2x + k, we have

∴ Remainder = (2k – 9)x – k(8 – k) + 10
But the remainder = x + a (Given)
Therefore, comparing them, we have

and a = -k(8 – k) + 10
= -5(8 – 5) + 10
= -5(3) + 10 = -15 + 10 = -5
Thus k = 5 and a = -5

In this article, we will share MP Board Class 10th Maths Book Solutions Chapter 12 Areas Related to Circles Ex 12.3 Pdf, These solutions are solved subject experts from the latest edition books.

MP Board Class 10th Maths Solutions Chapter 12 Areas Related to Circles Ex 12.3

Unless stated otherwise, use π = \(\frac{22}{7}\)

Question 1.
Find the area of the shaded region in the given figure, if PQ = 24 cm, PR = 7cm and O is the centre of the circle.

Solution:
Since O is the centre of the circle,
∴ QOR is a diameter.
⇒ ∠RPQ = 90° [Angle in a semicircle]
Now, in right ∆RPQ, RQ² = PQ²+ PR² [Pythagoras theorem]
⇒ RQ² = 24² + 7² = 576 + 49 = 625
⇒ RQ = \(\sqrt{625}\) = 25 cm
∴ Radius of a circle (r) = \(\frac{25}{2}\) cm
∴ Area of ∆RPQ
= \(\frac{1}{2}\) × PQ × RP = \(\frac{1}{2}\) × 24 × 7cm²
= 12 × 7 cm² = 84 cm²
Now, area of semicircle

∴ Area of the shaded portion
= 245.54 cm² – 84 cm² = 161.54 cm²

Question 2.
Find the area of the shaded region in given figure, if radii of the two concentric circles with centre O are 7 cm and 14 cm respectively and ∠AOC = 40°.

Solution:
Radius of the outer circle (R) = 14 cm and θ = 40°

Question 3.
Find the area of the shaded region in the given figure, if ABCD is a square of side 14 cm and APD and BPC are semicircles.

Solution:
Side of the square = 14 cm
∴ Area of the square ABCD = 14 × 14 cm²
= 196 cm²

Similarly, area of semi-circle BPC = 77 cm²
∴ Total area of two semi-circle = (77 + 77) cm²
= 154 cm²
Area of the shaded part
= Area of the square ABCD – Area of semi-circles
= (196 – 154) cm² = 42 cm²

Question 4.
Find the area of the shaded region in the figure, where a circular arc of radius 6 cm has been drawn with vertex O of an equilateral triangle OAB of side 12 cm as centre.

Solution:
Area of the equilateral triangle OAB

Question 5.
From each corner of a square of side 4 cm a quadrant of a circle of radius 1 cm is cut and also a circle of diameter 2 cm is cut as shown in the figure. Find the area of the remaining portion of the square.

Solution:
ABCD of the square ABCD = (4)² cm² = 16 cm².
Area of circel inside the square = πr²
= π × (1)² = π cm².

Question 6.
In a circular table cover of (he radius 32 cm, a design Is formed leaving an equilìtcral triangle ABC in the middle as shown in the figure. Find the area of the design (shaded region).

Solution:
Let O be the centre of a circular table and ABC be the equilateral triangle.
Then we draw OD ⊥ BC
In ∆OBD, we have: cos 60° = \(\frac{\mathrm{OD}}{\mathrm{OB}}\)

Question 7.
In the figure, ABCD is a square of side 14 cm. With centres A, B, C and D, four circles are drawn such that each circle touch externally two of the remaining three circles. Find the area of the shaded region.
Solution:
Each side of the square ABCD = 14 cm

Question 8.
The given figure depicts a racing track whose left and right ends are semicircular. The distance between the two inner parallel line segments is 60 m and they are each 106 m long. If the track is 10 m wide, find:

(i) the distance around the track along its inner edge.
(ii) the area of the track.
Solution:
The distance around the track along the inner edge = Perimeter of GHI + Perimeter JKL + GL + IJ
= (π × 30 + π × 30 + 106 + 106)
= (60π + 212) m
= (60 × \(\frac{22}{7}\) + 212)m = \(\frac{2804}{7}\) m.

Similarly, area of another circular path
BCDJKLB = 1100 m²
Area of rectangular path (ABLG) = 106 × 10
= 1060 m²
Similarly, area of another rectangular path
IJDE = 1060 m²
Total area of the track
= (1100 + 1100 + 1060 + 1060) m²
= (2200 + 2120) m² = 4320 m².

Question 9.
In the given figure, AB and CD are two diameters of a circle (with centre O) perpendicular to each other and OD is the diameter of the smaller circle. If OA = 7 cm, find the area of the shaded region.

Solution:
O is the centre of the circle and OA = 7 cm
⇒ AB = 2OA = 2 × 7 cm = 14 cm
∵ AB and CD are perpendicular to each other.
⇒ OC ⊥ AB and OC = OA = 7 cm
Area of ∆ABC = \(\frac{1}{2}\) × AB × OC
= \(\frac{1}{2}\) × 14 cm × 7cm = 49 cm²
Again, OD = OA = 7 cm
∴ Radius of the small circle = \(\frac{1}{2}\) (OD)

Question 10.
The area of an equilateral triangle ABC is 17320.5 cm². With each vertex of the triangle as centre, a circle is drawn with radius equal to half the length of the side of the triangle (see figure). Find the area of the shaded region. (Use π = 3.14 and \(\sqrt{3}\) = 1.73205).

Solution:
Area of ∆ABC = 17320.5 cm²

⇒ (side)² = 40000
⇒ (side)² = (200)²
⇒ side = 200 cm
∴ Radius of each circle = \(\frac{200}{2}\) cm = 100 cm
Since, each angle of an equilateral triangle is 60°,
∠A = ∠B = ∠C = 60°
Area of a sector having angle of sector (θ), as 60° and radius (r) = 100 cm = \(\frac{\theta}{360^{\circ}}\) × πr²

Now, area of the shaded region = [Area of the equilateral triangle ABC] – [Area of 3 equal sectors]
= 17320.5 cm² – 15700 cm² = 1620.5 cm²

Question 11.
On a square handkerchief, nine circular designs each of radius 7 cm are made (see figure). Find the area of the remaining portion of the handkerchief.

Solution:
∵ The circles touch each other.
∴ The side of the square ABCD
= 3 × diameter of a circle = 3 × (2 × radius of a circle) = 3 × (2 × 7) cm = 42 cm
⇒ Area of the square ABCD = 42 × 42 cm²
= 1764 cm²
Now, area of one circle
= πr² = \(\frac{22}{7}\) × 7 × 7 cm² = 154cm²
∴ Total area of 9 circles = 9 × 154 cm² = 1386 cm²
∴ Area of the remaining portion of the handkerchief = (1764 – 1386) cm² = 378 cm²

Question 12.
In the given figure, OACB is a quadrant of a circle with centre O and radius 3.5 cm. If OD = 2 cm, find the area of the
(i) quadrant OACB,
(ii) shaded region.

Solution:
(i) Here, radius (r) = 3.5 cm

Question 13.
In the given figure, a square OABC is inscribed in a quadrant OPBQuestion If OA = 20 cm, find the area of the shaded region (Use π = 3.14)

Solution:
OABC is a square such that its side
OA = 20 cm
∴ OB² = OA² + AB²
⇒ OB² = 20² + 20² = 400 + 400 = 800
⇒ OB = \(\sqrt{800}=20 \sqrt{2}\)
⇒ Radius of the quadrant (r) = \(20 \sqrt{2}\) cm
Now, area of the quadrant OPBQ = \(\frac{1}{4}\) πr²
= \(\frac{1}{4} \times \frac{314}{100}\) × 800 cm² = 314 × 2 = 628 cm²
Area of the square OABC = 20 × 20 cm² = 400 cm²
∴ Area of the shaded region
= 628 cm² – 400 cm² = 228 cm²

Question 14.
AB and CD are respectively arcs of two concentric circles of radii 21 cm and 7 cm and centre O (see figure). If ∠AOB = 30°, find the area of the shaded region.

Solution:
∵ Radius of bigger circle R = 21 cm and sector angle θ = 30°
∴ Area of the sector OAB

Question 15.
In the given figure, ABC is a quadrant of a circle of radius 14 cm and a semicircle is drawn with BC as diameter. Find the area of the shaded region.

Solution:
Radius of the quadrant = 14 cm
Since, BC is a diameter in a semi-circle.
∴ ∠BAC = θ = 90°
Area of the semicircle ABPC
= [\(\frac{90^{\circ}}{360^{\circ}} \times \frac{22}{7}\) × 14 × 14] cm²
= 22 × 7 cm² = 154 cm²
Area of right ∆ABC
= \(\frac{1}{2}\) × 14 × 14 cm² = 98 cm²
⇒ Area of segment BPC = 154 cm² – 98 cm²
= 56 cm²

Now, area of the shaded region = [Area of semicircle BQC] – [Area of segment BRC]
= 154 cm² – 56 cm² = 98 cm²

Question 16.
Calculate the area of the designed region in the given figure, common between the two quadrants of circles of radius 8 cm each.

Solution:
Side of the square = 8 cm
Area of the square ABCD = 8 × 8 cm² = 64 cm²
Now, radius of the quadrant ADQB = 8 cm
∴ Area of the quadrant ADQB

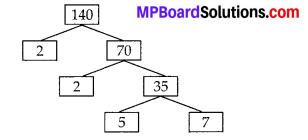
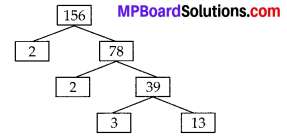
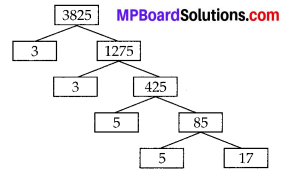
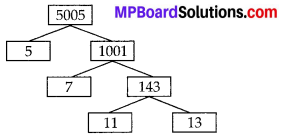
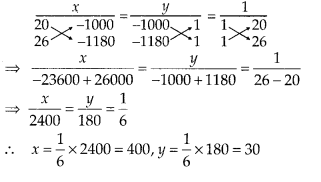In this article, we will share MP Board Class 10th Maths Book Solutions Chapter 1 Real Numbers Ex 1.3 Pdf, These solutions are solved subject experts from the latest edition books.

MP Board Class 10th Maths Solutions Chapter 1 Real Numbers Ex 1.3

Question 1.
Prove that \(\sqrt{5}\) is irrational.
Solution:
Let us assume, to the contrary, that \(\sqrt{5}\) is rational.
∴ \(\sqrt{5}=\frac{a}{b}\)
∴ b × \(\sqrt{5}\) = a
By Squaring on both sides,
5b² = a² …………. (i)
∴ 5 divides a².
5 divides a.
∴ We can write a = 5c.
Substituting the value of ‘a’ in eqn. (i),
5b² = (5c)² = 25c²
b² = 5c²
It means 5 divides b².
∴ 5 divides b.
∴ ‘a’ and ‘b’ have at least 5 as a common factor.
But this contradicts the fact that a’ and ‘b’ are prime numbers.
∴ \(\sqrt{5}\) is an irrational number.

Question 2.
Prove that 3 +2\(\sqrt{5}\) is irrational.
Solution:
Let 3 + 2\(\sqrt{5}\) is rational.

⇒ From (1), \(\sqrt{5}\) is rational
But this contradicts the fact that \(\sqrt{5}\) is irrational.
∴ Our supposition is wrong.
Hence, 3 + 2\(\sqrt{5}\) is irrational.

Question 3.
Prove that the following are irrationals.
(i) \(\frac{1}{\sqrt{2}}\)
(ii) 7\(\sqrt{5}\)
(iii) 6 + \(\sqrt{2}\)
Solution:
(i) We have

From (1), \(\sqrt{2}\) is rational number which contradicts the fact that \(\sqrt{2}\) is irrational.
∴ Our assumption is wrong.
Thus, \(\frac{1}{\sqrt{2}}\) is irrational.

(ii) Let \(7 \sqrt{5}\) is rational.
∴ We can find two co-prime integers a and b such that \(7 \sqrt{5}=\frac{a}{b}\), where b ≠ 0

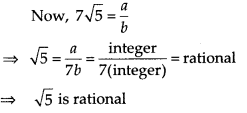
This contradicts the fact that \(\sqrt{5}\) is irrational.
∴ Out assumption is wrong.
Thus, we conclude that 7\(\sqrt{5}\) is irrational.

(iii) Let 6 + \(\sqrt{2}\) is rational.
∴ We can find two co-prime integers a and b

= Rational [ ∵ a and b are integers]
From (1), \(\sqrt{2}\) is a rational number,
which contradicts the fact that \(\sqrt{2}\) is an irrational number.
∴ Our supposition is wrong.
⇒ 6 + \(\sqrt{2}\) is an irrational number.

In this article, we will share MP Board Class 10th Maths Book Solutions Chapter 2 Polynomials Ex 2.1 Pdf, These solutions are solved subject experts from the latest edition books.

MP Board Class 10th Maths Solutions Chapter 2 Polynomials Ex 2.1

Question 1.
The graphs of y = p(x) are given in the below figures, for some polynomials p(x). Find the number of zeroes of p{x), in each case.

Solution:
(i) The given graph is parallel to x-axis, it does not intersect the x-axis.
It has no zero.
(ii) The given graph intersects the x-axis at one point only.
∴ It has one zero.
(iii) The given graph intersects the x-axis at three points.
∴ It has three zeroes.
(iv) The given graph intersects the x-axis at two points.
∴ It has two zeroes.
(v) The given graph intersects the x-axis at four points.
∴ It has four zeroes.
(vi) The given graph meets the x-axis at three points.
∴ It has three zeroes.

In this article, we will share MP Board Class 10th Maths Book Solutions Pair of Linear Equations in Two Variables Ex 3.6 Pdf, These solutions are solved subject experts from the latest edition books.

MP Board Class 10th Maths Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.6

Question 1.
Solve the following pairs of equations by reducing them to a pair of linear equations:


Solution:
(i) we have


Equations (1) and (2) becomes,
2u + 3v = 2 ⇒ 2u + 3v – 2 = 0 … (3)
4u – 9v = -1 ⇒ 4u – 9v + 1 = 0 … (4)

(iii)

The equations (1) and (2) becomes,
4p + 3y = 14 ⇒ 4y + 3y -14 = 0 …. (3)
3p – 4y = 23 ⇒ 3p – 4y – 23 = 0 …. (4)
Here, a₁ = 4, b₁= 3, c₁ = —14, a₂ = 3, b₂ = – 4, c₂ = -23
Solving (3) and (4) by cross multiplication method, we get

(iv)

Equations (1) and (2) can be expressed
5u + v = 2 ⇒ 5u + v – 2 = 0 …. (3)
6u – 3v = 1 ⇒ 6u – 3v – 1 = 0 …. (4)

Thus, the required solution is x = 4, y = 5

(v)

∴ Equation (3)and (4)can be expressed as:
7q – 2p – 5 = 0 … (5)
8q + 7p -15 = 0 … (6)

Thus, the required solution is x = 1, y = 1

(vi) We have, 6x + 3y = 6xy …. (1)
2x + 4y = 5xy … (2)
From (1) , we get

2q + 4p = 5 ….(6)
Multiply (6) by 3, we get
6q +12p = 15 … (7)
Subtracting (5) from (7) , we get
6q + 12p – 6q – 3p = 15 – 6
9p = 9 ⇒ p = 1
Now, Substituting, p = 1 in (5) , we get
6q + 3(1) = 6

∴ Equations (1) and (2) can be expressed as :
10p + 2q = 4 = ⇒ 10p + 2q – 4 = 0 …(3)
15p – 5q = -2 ⇒ 15p – 5q + 2 = 0 … (4)

⇒ 2x = 6 ⇒ x = 3
Now, substituting the value of x in equation (5) , we get
3 + y = 5 ⇒ y = 2
Thus, the required solution is x = 3, y = 2

(viii)

Question 2.
Formulate the following problems as a pair of equations, and hence find their solutions:
(i) Ritu can row downstream 20 km in 2 hours, and upstream 4 km in 2 hours. Find her speed of rowing in still water and the speed of the current.
(ii) 2 women and 5 men can together finish an embroidery work in 4 days, while 3 women and 6 men can finish it in 3 days. Find the time taken by 1 woman alone to finish the work, and also that taken by 1 man alone.
(iii) Roohi travels 300 km to her home partly by train and partly by bus. She takes 4 hours if she travels 60 km by train and the remaining by bus. If she travels 100 km by train and the remaining by bus, she takes 10 minutes longer. Find the speed of the train and the bus separately.
Solution:
(i) Let the speed of Ritu in still water = x km/hr
and the speed of the current = y km/hr
∴ Downstream speed = (x + y) km/hr
Upstream speed = (x – y)km/hr

Substituting the value of x in equation (1), we get
6 + y = 10 ⇒ y = 10 – 6 = 4
Thus, speed of rowing in still water = 6 km/hr, speed of current = 4 km/hr

(ii) Let the time taken to finish the task by one woman alone = x days
and the time taken to finish the task by one man alone = y days


∴ 1 man can finish the work in 36 days and 1 woman can finish the work in 18 days,

(iii) Let the speed of the train = x km/hr
and the speed of the bus = y km/hr

Case I: Total journey = 300 km
Distance travelled by train = 60 km
Distance travelled by bus = (300 – 60)km
= 240 km
∵ Total time taken = 4 hours

Case II: Distance travelled by train = 100 km
Distance travelled by bus = (300 – 100)km
= 200 km
Total time = 4 hrs 10 mins

Thus, speed of the train = 60 km/hr
and speed of the bus = 80 km/hr

In this article, we will share MP Board Class 10th Maths Book Solutions Chapter 1 Real Numbers Ex 1.2 Pdf, These solutions are solved subject experts from the latest edition books.

MP Board Class 10th Maths Solutions Chapter 1 Real Numbers Ex 1.2

Question 1.
Express each number as a product of its prime factors:
(i) 140
(ii) 156
(iii) 3825
(iv) 5005
(v) 7429
Solution:
(i) Using factor tree method, we have

∴ 140 = 2 × 2 × 5 × 7 = 22 × 5 × 7

(ii) Using factor tree method, we have

∴ 156 = 2 × 2 × 3 × 13 = 22 × 3 × 13

(iii) Using factor tree method, we have

3825 = 3 × 3 × 5 × 5 × 17 = 32 × 52 × 17

(iv) Using factor tree method, we have

∴ 5005 = 5 × 7 × 11 × 13

(v) Using factor tree method, we have

∴ 7429 = 17 × 19 × 23

Question 2.
Find the LCM and HCF of the following pairs of integers and verify that LCM × HCF = product of the two numbers.
(i) 26 and 91
(ii) 510 and 92
(iii) 336 and 54
Solution:
(i) Using factor tree method, we have

⇒ 26 = 2 × 13 and 91 = 7 × 13
LCM of 26 and 91 = 2 × 7 × 13 = 182
HCF of 26 and 91 = 13 Now,
LCM × HCF = 182 × 13 = 2366 and 26 × 91 = 2366
i. e., LCM × HCF = Product of two numbers,

(ii) Using the factor tree method, we have

⇒ 510 = 2 × 3 × 5 × 17 and 92 = 2 × 2 × 23
∴ LCM of 510 and 92 = 2 × 2 × 3 × 5 × 17 × 23 = 23460
HCF of 510 and 92 = 2 LCM × HCF
= 23460 × 2 = 46920 and 510 × 92 = 46920
i. e., LCM × HCF = Product of two numbers.

(iii) Using the factor tree method, we have

336 = 2 × 2 × 2 × 2 × 3 × 7
54 = 2 × 3 × 3 × 3
LCM of 336 and 54
= 2 × 2 × 2 × 2 × 3 × 3 × 3 × 7 = 3024
HCF of 336 and 54 = 2 × 3 = 6
LCM × HCF = 3024 × 6 = 18144
Also 336 × 54 = 18144
Thus, LCM × HCF = Product of two numbers.

Question 3.
Find the LCM and HCF of the following integers by applying the prime factorisation method.
(i) 12,15 and 21
(ii) 17,23 and 29
(iii) 8,9 and 25
Solution:
(i) We have

⇒ 12 = 2 × 2 × 3, 15 = 3 × 5 and 21 = 3 × 7
∴ HCF of 12, 15 and 21 is 3
LCM of 12,15 and 21 is 2 × 2 × 3 × 5 × 7 i.e., 420

(ii) We have
17 = 1 × 17, 23 = 1 × 23, 29 = 1 × 29
⇒ HCF of 17, 23 and 29 is 1 LCM of 17, 23 and 29 = 17 × 23 × 29 = 11339

(iii) We have

⇒ 8 = 2 × 2 × 2, 9 = 3 × 3 and 25 = 5 × 5
∴ HCF of 8, 9 and 25 is 1
LCM of 8, 9 and 25 is 2 × 2 × 2 × 3 × 3 × 5 × 5 = 1800

Question 4.
Given that HCF (306, 657) = 9, find LCM (306, 657).
Solution:
H.C.F × L.C.M = a × b
(a, b) × (a, b) = a × b
9 × x = 306 × 657
x = \(\frac{306 \times 657}{9}\)
∴ x = 22338
∴ L.C.M of (306, 657) = 22338

Question 5.
Check whether 6″ can end with the digit 0 for any natural number n.
Solution:
Here, n is a natural number and let 6ⁿ ends with digit 0.
∴ 6ⁿ is divisible by 5.
But the prime factors of 6 are 2 and 3. i.e.,
6 = 2 × 3
⇒ 6ⁿ = (2 × 3)ⁿ
i. e., In the prime factorisation of 6ⁿ, there is no factor 5.
So, by the fundamental theorem of Arithmetic, every composite number can be expressed as a product of primes and this factorisation is unique apart from the order in which the prime factorisation occurs.
∴ Our assumption that 6ⁿ ends with digit 0, is wrong.
Thus, there does not exist any natural number n for which 6ⁿ ends with zero.

Question 6.
Explain why 7 × 11 × 13 + 13 and 7 × 6 × 5 × 4 × 3 × 2 × 1 + 5 are composite numbers.
Solution:
i) 7 × 11 × 13 + 13 = 13(77 + 1)
= 13 × 78
∴ It is a composite number
[It is having more than two factors]

ii) 7 × 6 × 5 × 4 × 3 × 2 × 1 + 5
=5[7 × 6 × 4 × 3 × 2 × 1 + 1]
= 5 (1008 + 1)
= 5 × 1009 = 5045
∴ It is a composite number.

Question 7.
There is a circular path around a sports field. Sonia takes 18 minutes to drive one round of the field, while Ravi takes 12 minutes for the same. Suppose they both start at the same point and at the same time, and go in the same direction. After how many minutes will they meet again at the starting point?
Solution:
Time taken by Sonia to drive one round of the field = 18 minutes
Time taken by Ravi to drive one round of the field = 12 minutes
The LCM of 18 and 12 gives the exact number of minutes after which they meet again at the starting point.
We have

⇒ 18 = 2 × 3 × 3 and 12 = 2 × 2 × 3
∴ LCM of 18 and 12 = 2 × 2 × 3 × 3 = 36
Thus, they will meet again at the starting point after 36 minutes.